普利姆(Prim)算法是以某个顶点为起点,逐步寻找各个顶点上权值最小的边来构建生成树。
文章指引:图—普里姆(Prim)算法(原理和C程序解释)
而克鲁斯卡尔(Kruskal)算法是以边为目标,直接寻找权值最小的边来构建生成树,并在构建中不形成回路。
一、定义
假设N = (V, {E})是一个连通网,则令最小生成树的初始状态为只有n个顶点而无边的非连通图T = {V, {}},图中每个顶点自成一个连通分量。
在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。依次类推,直至T中所有顶点都在同一连通分量上为止。
二、实现思路
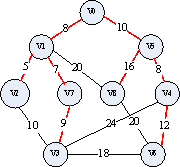
下图是一个连通网,我们以此来介绍普利姆算法的实现过程。
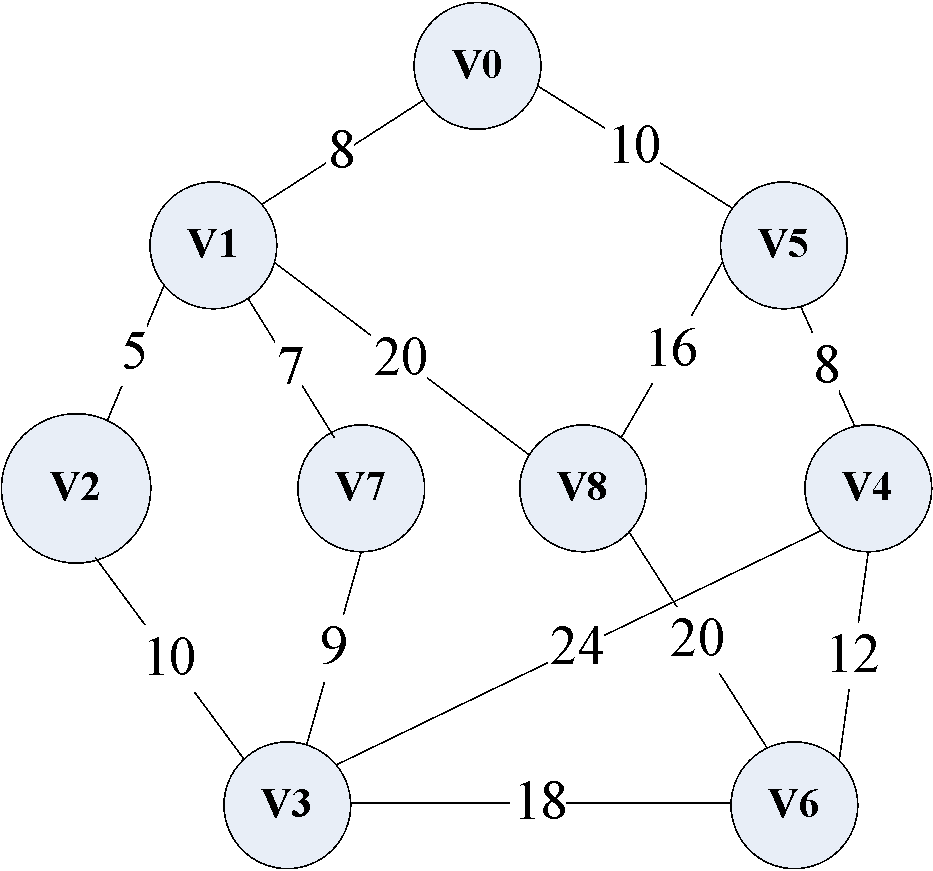
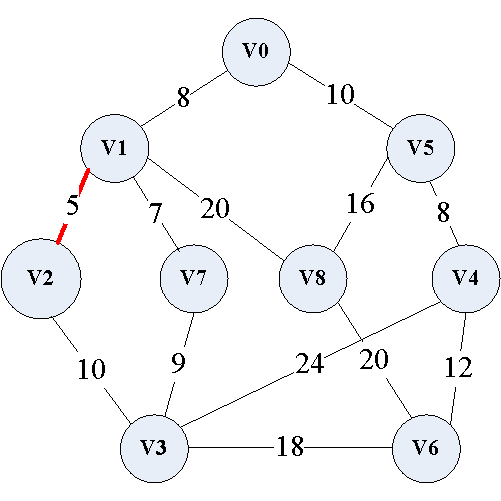
(1)首先设立最小生成树的初始状态T = {V, {}},只有顶点,没有边,寻找权值最小的边,显然是 ( v 1 , v 5 ) (v_1,v_5) (v1,v5)最小。
注:红色边为最小生成树的边,黑色线为连通网的边。
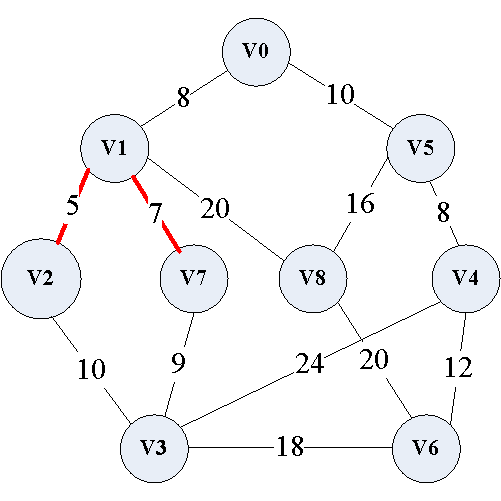
(2)然后 ( v 1 , v 7 ) (v_1,v_7) (v1,v7)边权值最小
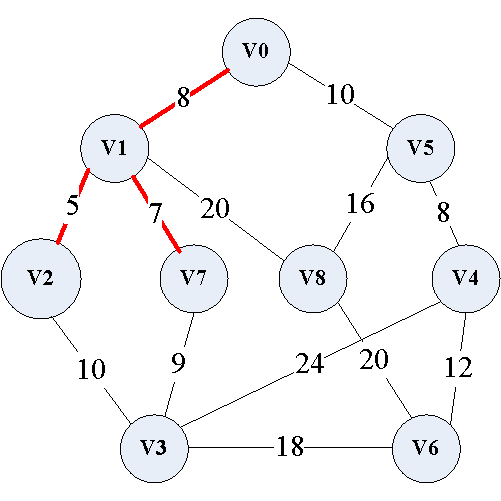
(3)此时有两条边的权值均为8,这里先取 ( v 0 , v 1 ) (v_0,v_1) (v0,v1)边
(4)添加 ( v 4 , v 5 ) (v_4,v_5) (v4,v5)边
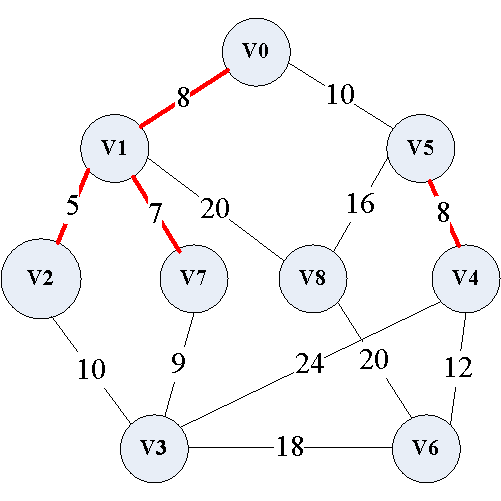
(5)添加 ( v 3 , v 7 ) (v_3,v_7) (v3,v7)边
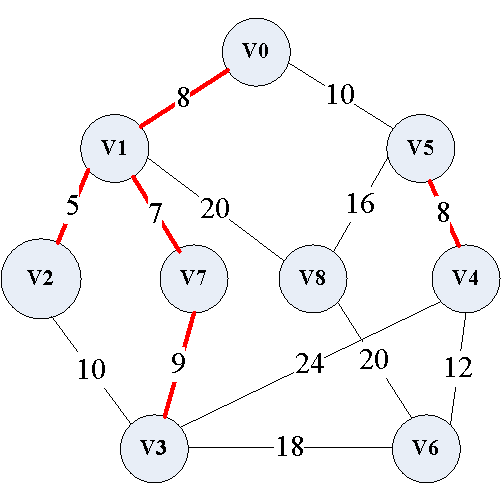
(6)因为 ( v 2 , v 3 ) (v_2,v_3) (v2,v3)边的两个顶点在同一连通分量中,如果添加此边,则会形成回路,所以添加 ( v 0 , v 5 ) (v_0,v_5) (v0,v5)边
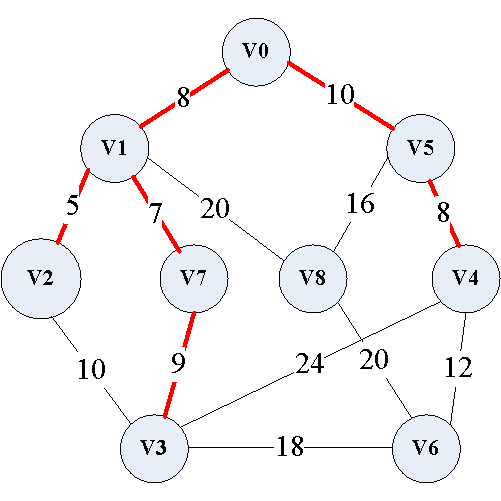
(7)添加 ( v 4 , v 6 ) (v_4,v_6) (v4,v6)边
(8)添加 ( v 5 , v 8 ) (v_5,v_8) (v5,v8)边
此时所有顶点都在同一连通分量上,红色边所有顶点构造的树即为最小生成树。
三、程序解析
1. 临接矩阵转换为边集数组
(1)因为无向图的邻接矩阵是对称矩阵,那么边集数组只需要统计矩阵的右上半即可。edge[]用于存储图的每一条边。
(2)对边安装权值排序,由大到小,这里使用比较简单的冒泡排序法。
//邻接矩阵转边集数组,按照权值排序,由小到大
void MGraph2EdgeArr(MGraph G, Edge* edge)
{
int i, j, k=0;
Edge temp;
//将边数据填入edge中
for (i = 0; i < G.numVertexes; i++)
{
for (j = i + 1; j < G.numVertexes; j++)
{
if (G.arc[i][j] != INFINITY) //有边
{
edge[k].begin = i;
edge[k].end = j;
edge[k].weight = G.arc[i][j];
k++;
}
}
}
//冒泡排序
for (i = 0; i < k; i++)
{
for (j = i+1; j < k; j++)
{
if (edge[j].weight < edge[i].weight)
{
temp = edge[i];
edge[i] = edge[j];
edge[j] = temp;
}
}
}
}
2. 克鲁斯卡尔算法程序
(1)parent数组:将同一连通分量的顶点串起来,下标为edge.begin,即各边的尾顶点下标,parent存储的值是边的头顶点下标,如果某一个顶点是两个边的尾,则在上一个边的头顶点位置存储下一个边的头顶点下标。
比如最小生成树依次添加了
(
v
1
,
v
2
)
(v_1,v_2)
(v1,v2),
(
v
1
,
v
7
)
(v_1,v_7)
(v1,v7),
(
v
0
,
v
1
)
(v_0,v_1)
(v0,v1),此时parent发生如下变化:
在添加 ( v 1 , v 7 ) (v_1,v_7) (v1,v7)关系时,因为 p a r e n t [ 1 ] = 2 parent[1] = 2 parent[1]=2, p a r e n t [ 2 ] = 0 parent[2] = 0 parent[2]=0,因此使 p a r e n t [ 2 ] = 7 parent[2] = 7 parent[2]=7。

如何判断两个顶点是否在同一连通分量呢?
可以根据parent观察,因为
p
a
r
e
n
t
[
0
]
=
7
,
p
a
r
e
n
t
[
7
]
=
0
parent[0] = 7,\ parent[7] = 0
parent[0]=7, parent[7]=0,所以
v
0
,
v
7
v_0, v_7
v0,v7在同一分量中,取名为连通分量A;因为
p
a
r
e
n
t
[
1
]
=
2
,
p
a
r
e
n
t
[
2
]
=
7
parent[1] = 2, \ parent[2] = 7
parent[1]=2, parent[2]=7,所以
v
1
,
v
2
,
v
7
v_1, v_2, v_7
v1,v2,v7,它们均在连通分量A中。
我们只需要判断连线顶点的结尾顶点是否相同,如 v 1 , v 2 v_1,v_2 v1,v2连线均以 v 7 v_7 v7为结尾。
(2)按照权值从小到大遍历所有边,Find函数查找边的两端顶点所在的连通分量的结尾顶点,如果不同,则认为可以将此边添加到最小生成树中,不存在回路,打印该边信息。更新parent信息,将两个顶点所在的连通分量连接起来。
typedef struct // 边集结构
{
int begin;
int end;
int weight;
}Edge;
#define MAXEDGE (15) //最大边数
void MiniSpanTree_Kruskal(MGraph G)
{
int i, n, m;
Edge edges[MAXEDGE]; //定义边集数组
int parent[MAXEDGE]; //定义一数组用来判断边与边是否形成环路
MGraph2EdgeArr(G, edges); //将邻接矩阵转换为边集数组
for (i = 0; i < G.numEdges; i++)
{
parent[i] = 0; //初始化数组值为0
}
for (i = 0; i < G.numEdges; i++)
{
n = Find(parent, edges[i].begin);
m = Find(parent, edges[i].end);
if (n != m) //判断edges[i].begin和edges[i].end是否在同一连通分量中
{
parent[n] = m; //将edges[i].begin与edges[i].end连线
printf(" (%d, %d) %d ", edges[i].begin, edges[i].end, edges[i].weight);
}
}
}
/* 查找连线顶点的尾部下标 */
int Find(int* parent, int f)
{
while (parent[f] > 0)
{
f = parent[f];
}
return f;
}
3. 测试
#include "CreateGraph.h"
#include "kruskal.h"
int main()
{
MGraph G;
CreateMgraph(&G);
MiniSpanTree_Kruskal(G);
return 0;
}
打印输出:

四、总结
因为Find函数的时间复杂度为 O ( l o g e ) O(loge) O(loge),e为连通网的边数,且for循环e次,则卡鲁斯卡尔的时间复杂度为 O ( e l o g e ) O(eloge) O(eloge)。该算法主要针对边来展开,因此对于边数少的连通网来说,效率比较高。





 本文详细介绍了克鲁斯卡尔算法的原理和实现过程,从定义、思路到C语言程序解析,包括边集数组的构建和防止形成回路的判断。最后通过一个连通网实例展示了算法的运行步骤,总结了算法的时间复杂度。
本文详细介绍了克鲁斯卡尔算法的原理和实现过程,从定义、思路到C语言程序解析,包括边集数组的构建和防止形成回路的判断。最后通过一个连通网实例展示了算法的运行步骤,总结了算法的时间复杂度。
















 1770
1770


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







