JZ12 矩阵中的路径：用来判断在一个n乘m的矩阵中是否存在一条包含某长度为len的字符串所有字符的路径。

题目描述
请设计一个函数，用来判断在一个n乘m的矩阵中是否存在一条包含某长度为len的字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。 例如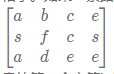
矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

示例1
输入：
[[a,b,c,e],[s,f,c,s],[a,d,e,e]],“abcced”

返回值：
true

示例2
输入：
[[a,b,c,e],[s,f,c,s],[a,d,e,e]],“abcb”

返回值：
false

回溯算法解决

回溯算法实际上一个类似枚举的搜索尝试过程，也就是一个个去试，我们解这道题也是通过一个个去试。

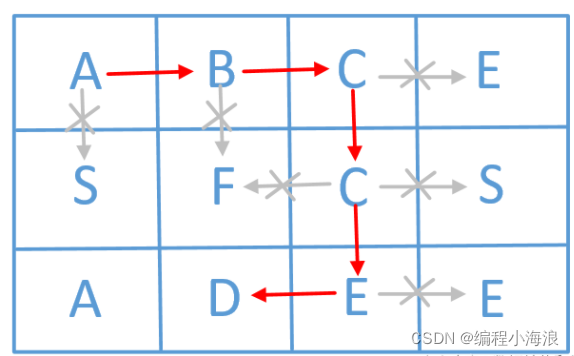
我们看到他是从矩形中的一个点开始往他的上下左右四个方向查找，这个点可以是矩形中的任何一个点，所以代码的大致轮廓我们应该能写出来，就是遍历矩形所有的点，然后从这个点开始往他的4个方向走，因为是二维数组，所以有两个for循环。

package com.example.hello.util;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * @param matrix char字符型二维数组
     * @param word   string字符串
     * @return bool布尔型
     */
    private boolean backtrack(char[][] matrix, String word, int index, int i, int j) {
        //回溯法求解
        if (index == word.length()) {
            //成功的出口
            return true;
        }
        //搜索到边界了
        if (i < 0 || i >= matrix.length || j < 0 || j >= matrix[0].length) return false;

        if (word.charAt(index) == '&') {
            //已经搜索过了
            return false;
        }
        if (word.charAt(index) == matrix[i][j]) {
            //当前字符匹配，搜索邻近结点
            char temp = matrix[i][j];
            //标记为已经搜索过
            matrix[i][j] = '&';
            boolean res = backtrack(matrix, word, index + 1, i - 1, j) ||
                    backtrack(matrix, word, index + 1, i + 1, j) ||
                    backtrack(matrix, word, index + 1, i, j - 1) ||
                    backtrack(matrix, word, index + 1, i, j + 1);
            //恢复
            matrix[i][j] = temp;
            return res;
        }
        return false;
    }

    public boolean hasPath(char[][] matrix, String word) {
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++)
                if (backtrack(matrix, word, 0, i, j)) {
                    return true;
                }
        }
        return false;

    }

    public static void main(String[] args) {
        char[][] matrix = {
                {'a', 'b', 'c', 'e'},
                {'s', 'f', 'c', 's'},
                {'a', 'd', 'e', 'e'}};
        String word = "see";
        Solution solution = new Solution();
        System.out.println(solution.hasPath(matrix, word));
    }
}