两个相交链表

最新推荐文章于 2025-03-23 20:19:03 发布

原创最新推荐文章于 2025-03-23 20:19:03 发布 · 700 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

本文详细探讨了单链表相交问题，包括无环和有环链表的相交判断，提供了判断方法和解决方案，适用于不同类型的链表结构。

两个单链表相交的一系列问题
【题目】在本题中，单链表可能有环，也可能无环。给定两个单链表的头节点 head1和head2，这两个链表可能相交，也可能
不相交。请实现一个函数，如果两个链表相交，请返回相交的第一个节点；如果不相交，返回null 即可。要求：如果链表1
的长度为N，链表2的长度为M，时间复杂度请达到 O(N+M)，额外空间复杂度请达到O(1)。

单链表的相交的情况:

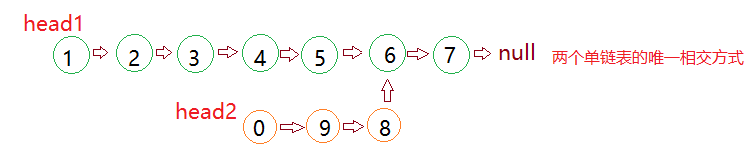
两个无环单链表相交时,他们的末尾节点一定是相同的
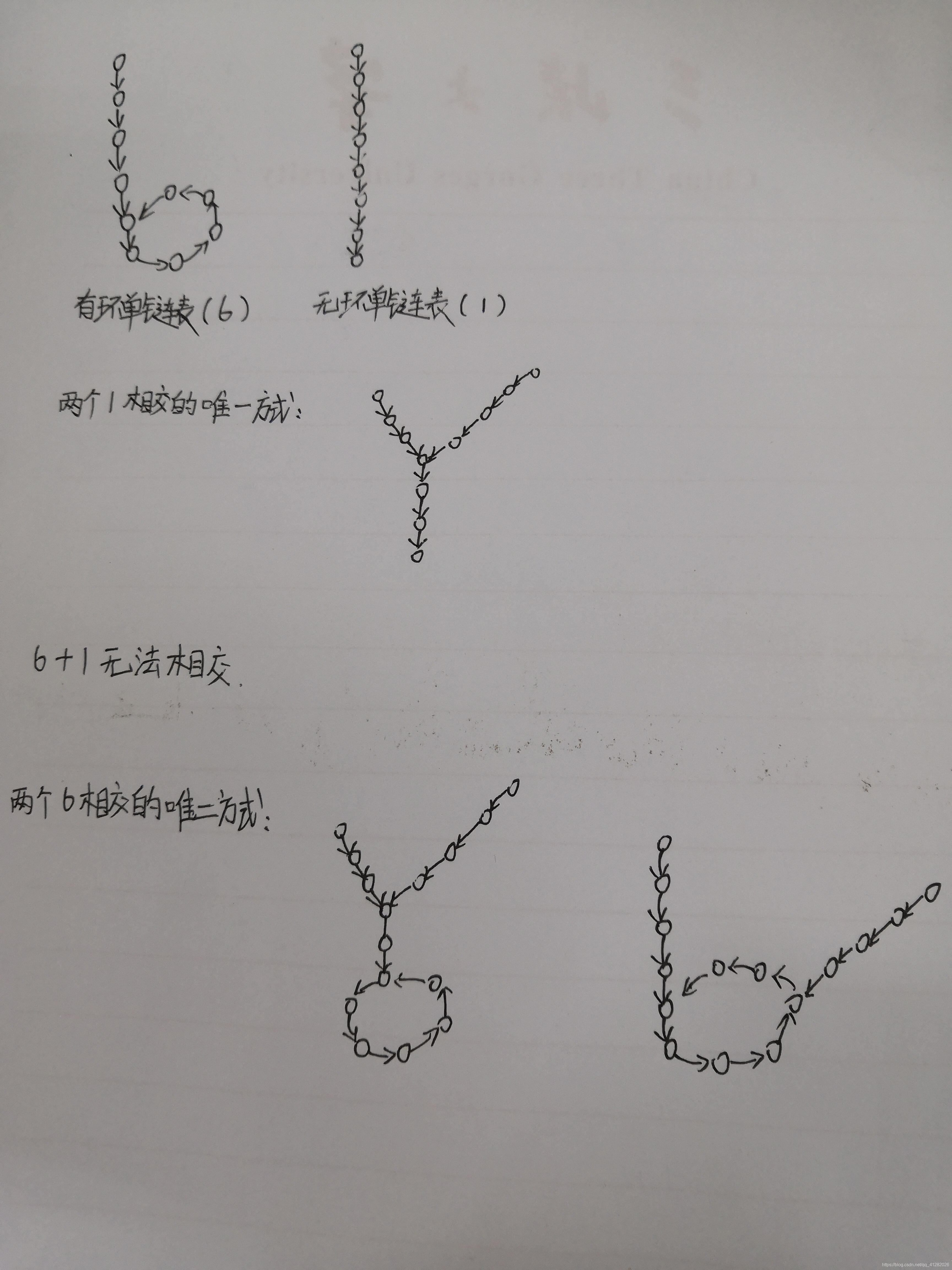
一个有环链表和一个无环链表是无法相交的
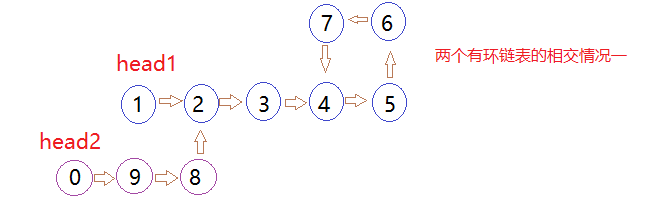
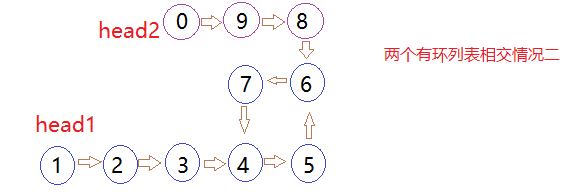
两个有环链表有两种相交的方式

判断两个链表是有环还是无环

方式一：判断链表是否有环可以通过一个map来实现：遍历链表，判断该节点是否在map，如果存在，则表明该节点是入环的节点；如果不存在，就把该节点放入map集合中，遍历完都没有碰见相同的节点，则表明该链表无环。

方式二：设置两个指针，一个快指针一次走两步、一个慢指针一次走一步。遍历链表，如果两个指针相遇了，即表明该链表是有环的，而且相遇的节点在环上，并且该节点到入环点的距离与头节点到入环点的距离是相等的，那么可以让快指针重新指向头节点，速度与慢指针一样一次一步，当两个指针再次相遇时，则表明相遇的节点即为入环点；如果快指针走到头了（null），则表明该链表是无环链表。

根据有环无环的情况分出三类情况分别进行判断

判断两个无环单链表是否相交
分别遍历两个无环单链表，得出各自的长度和尾节点。
如果尾节点相等，则表明相交，此时拿长链表的长度减去短链表的长度，长链表先走这个差值的步数，然后两个链表一起走，他们相遇时的节点即为相交节点
如果两个链表的尾节点不相等，则表明这两个单链表不相交。

判断两个有环单链表是否相交
先比较两个有环单链表的入环节点，如果入环节点相等，则表明两个链表是相交的，为图中的第二种情况，此时除去环，就是两个无环单链表的相交的情况，同上的步骤
如果入环节点不相等，则可能是相交也可能是不相交的，此时遍历其中一个单链表，如果在遍历的过程中碰到了另外一个单链表的入环节点，则表明这两个有环单链表是相交的（图中第三中情况，无论哪个入环节点都可以算作第一个相交点）；遍历完后，都没有碰见另外一个链表的入环节点，则表明是不相交的。

一个无环单链表和一个有环单链表无法相交

package struct;

public class FindFirstIntersectNode {

    //节点类
    public static class Node {

        int data;
        Node next;

        public Node (int data){ this.data = data; }

    }

    //主体方法
    public static Node getIntersectNode(Node head1,Node head2){
        if(head1 == null || head2 == null){
            return null;
        }

        //获取到两个链表的入环节点
        Node loop1 = getLoopNode(head1);
        Node loop2 = getLoopNode(head2);

        if(loop1 == null && loop2 == null){             //两个都是无环链表
            return noLoop(head1,head2);
        } else if(loop1 != null && loop2 != null){      //两个都是有环列表
            return bothLoop(head1,loop1,head2,loop2);
        } else {                                        //一个有环列表,一个无环列表:绝不会相交
            return null;
        }
    }

    //获取一个单链表的入环节点;没有环,则返回null
    public static Node getLoopNode(Node head) {
        if(head == null || head.next == null|| head.next.next == null){
            return null;
        }

        //设置两个指针
        Node small = head.next;
        Node fast = head.next.next;

        //如果有环,快指针与慢指针终会在环上相遇
        while(small != fast){
            //快指针走到头了,还没相遇,则表明没有环
            if(fast.next == null || fast.next.next == null){
                return null;
            }
            small = small.next;
            fast = fast.next.next;
        }

        //相遇后,快指针指向头节点,且与慢指针保持一样的速度,那么它们会在如环节点相遇
        fast = head;
        while(small != fast){
            small = small.next;
            fast = fast.next;
        }

        //返回入环节点
        return small;

    }

    //两个链表都是没有环
    public static Node noLoop(Node head1, Node head2) {
        if(head1 == null || head2 == null){
            return null;
        }

        Node cur1 = head1;
        Node cur2 = head2;
        int len = 0;

        //得到链表的长度,并且得到尾节点
        while(cur1.next != null){
            cur1 = cur1.next;
            len++;
        }

        //得到该链表与上一个链表的长度的差值,并且得到尾节点
        while(cur2.next != null){
            cur2 = cur2.next;
            len--;
        }

        //两个单链表的尾节点不相等,则表明没有相交
        if(cur1 != cur2){
            return null;
        }

        //两个单链表相交
        cur1 = len > 0 ? head1 : head2;                 //cur1指向长链表的头结点
        cur2 = cur1 == head1 ? head2 : head1;           //cur2指向另外一个链表的头结点
        len = Math.abs(len);                            //长度差值取绝对值

        //先让长链表走差值步
        while(len != 0){
            cur1 = cur1.next;
            len--;
        }

        while(cur1 != cur2){
            cur1 = cur1.next;
            cur2 = cur2.next;
        }

        //得到入环节点
        return cur1;

    }

    //两个链表都是有环链表
    public static Node bothLoop(Node head1,Node loop1,Node head2,Node loop2){

        Node cur1 = null;
        Node cur2 = null;

        //入环节点相等时,两个单链表相交
        if(loop1 == loop2){
            cur1 = head1;
            cur2 = head2;
            int len = 0;

            while(cur1 != loop1){
                len++;
                cur1 = cur1.next;
            }

            while(cur2 != loop2){
                len--;
                cur2 = cur2.next;
            }

            cur1 = len > 0 ? head1 : head2;
            cur2 = cur1 == head1 ? head2 : head1;
            len = Math.abs(len);

            while(len != 0){
                cur1 = cur1.next;
                len--;
            }
            while(cur1 != cur2){
                cur1 = cur1.next;
                cur2 = cur2.next;
            }
            return cur1;
        } else {                                    //两个单链表的入环节点不相等时,都有可能
            cur1 = loop1.next;
            while(cur1 != loop1){
                if(cur1 == loop2){
                    return loop1;
                }
                cur1 = cur1.next;
            }
            return null;
        }
    }

    public static void main(String[] args) {
        // 1->2->3->4->5->6->7->null
        Node head1 = new Node(1);
        head1.next = new Node(2);
        head1.next.next = new Node(3);
        head1.next.next.next = new Node(4);
        head1.next.next.next.next = new Node(5);
        head1.next.next.next.next.next = new Node(6);
        head1.next.next.next.next.next.next = new Node(7);

        // 0->9->8->6->7->null
        Node head2 = new Node(0);
        head2.next = new Node(9);
        head2.next.next = new Node(8);
        head2.next.next.next = head1.next.next.next.next.next; // 8->6
        System.out.println(getIntersectNode(head1, head2).data);

        // 1->2->3->4->5->6->7->4...
        head1 = new Node(1);
        head1.next = new Node(2);
        head1.next.next = new Node(3);
        head1.next.next.next = new Node(4);
        head1.next.next.next.next = new Node(5);
        head1.next.next.next.next.next = new Node(6);
        head1.next.next.next.next.next.next = new Node(7);
        head1.next.next.next.next.next.next = head1.next.next.next; // 7->4

        // 0->9->8->2...
        head2 = new Node(0);
        head2.next = new Node(9);
        head2.next.next = new Node(8);
        head2.next.next.next = head1.next; // 8->2
        System.out.println(getIntersectNode(head1, head2).data);

        // 0->9->8->6->7->4->5->6..
        head2 = new Node(0);
        head2.next = new Node(9);
        head2.next.next = new Node(8);
        head2.next.next.next = head1.next.next.next.next.next; // 8->6
        System.out.println(getIntersectNode(head1, head2).data);

    }

}