我的LeetCode代码仓:https://github.com/617076674/LeetCode
原题链接:https://leetcode-cn.com/problems/ugly-number-ii/
题目描述:

知识点:动态规划
思路一:暴力破解法(在LeetCode中提交会超时)
从0开始依次判断每一个数是否是丑数,每次递增1,直到找到第n个丑数。
时间复杂度是O(n ^ 2)。空间复杂度是O(1)。
JAVA代码:
public class Solution {
public int nthUglyNumber(int n) {
int index = 0, i = 0;
while (index < n) {
if (isUgly(i++)) {
index++;
}
}
return i - 1;
}
private boolean isUgly(int num) {
if (0 >= num) {
return false;
}
while (0 == num % 2) {
num /= 2;
}
while (0 == num % 3) {
num /= 3;
}
while (0 == num % 5) {
num /= 5;
}
if (1 == num) {
return true;
} else {
return false;
}
}
}
思路二:暴力破解法二
在思路一中,我们选择判断每一个数是否是偶数的方式来寻找第n个丑数。事实上我们完全可以换个思路,我们将所有的丑数先生成出来,再对其进行排序操作即可。
时间复杂度是O(nlogn)。空间复杂度是O(n)。
JAVA代码:
public class Solution {
public int nthUglyNumber(int n) {
ArrayList<Integer> arrayList = new ArrayList<>();
for (long i = 1; i < Integer.MAX_VALUE; i *= 2) {
for (long j = i; j < Integer.MAX_VALUE; j *= 3) {
for (long k = j; k < Integer.MAX_VALUE; k *= 5) {
arrayList.add((int) k);
}
}
}
Collections.sort(arrayList);
return arrayList.get(n - 1);
}
}
LeetCode解题报告:
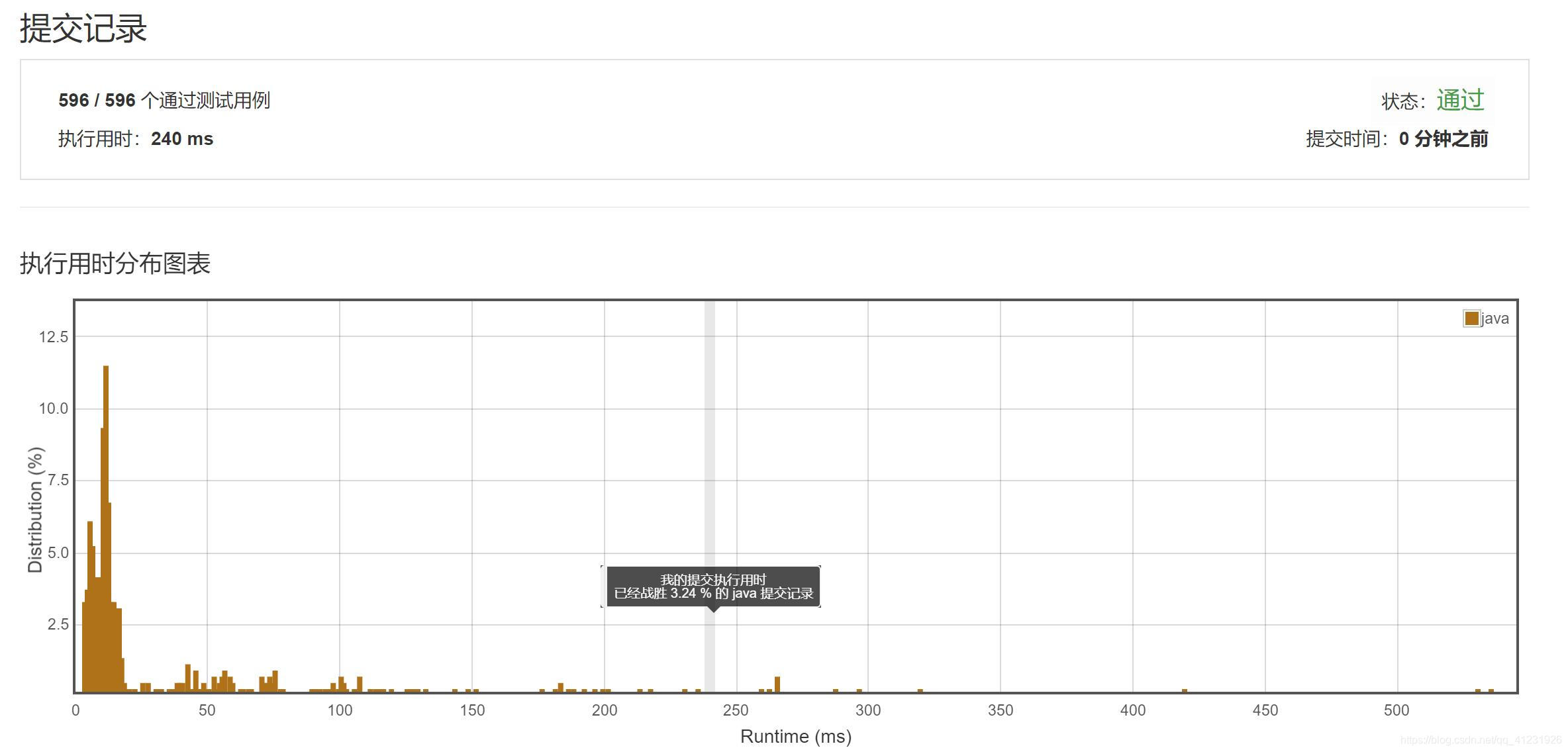
思路三:思路二的改进
我们将思路二中生成所有丑数并对其进行排序的过程放入一个静态代码块中,这样该过程的时间就不会计入程序运行时间里。
时间复杂度是O(1)。空间复杂度是O(n)。
JAVA代码:
public class Solution {
private static ArrayList<Integer> arrayList = new ArrayList<>();
static {
for (long i = 1; i < Integer.MAX_VALUE; i *= 2) {
for (long j = i; j < Integer.MAX_VALUE; j *= 3) {
for (long k = j; k < Integer.MAX_VALUE; k *= 5) {
arrayList.add((int) k);
}
}
}
Collections.sort(arrayList);
}
public int nthUglyNumber(int n) {
return arrayList.get(n - 1);
}
}
LeetCode解题报告:
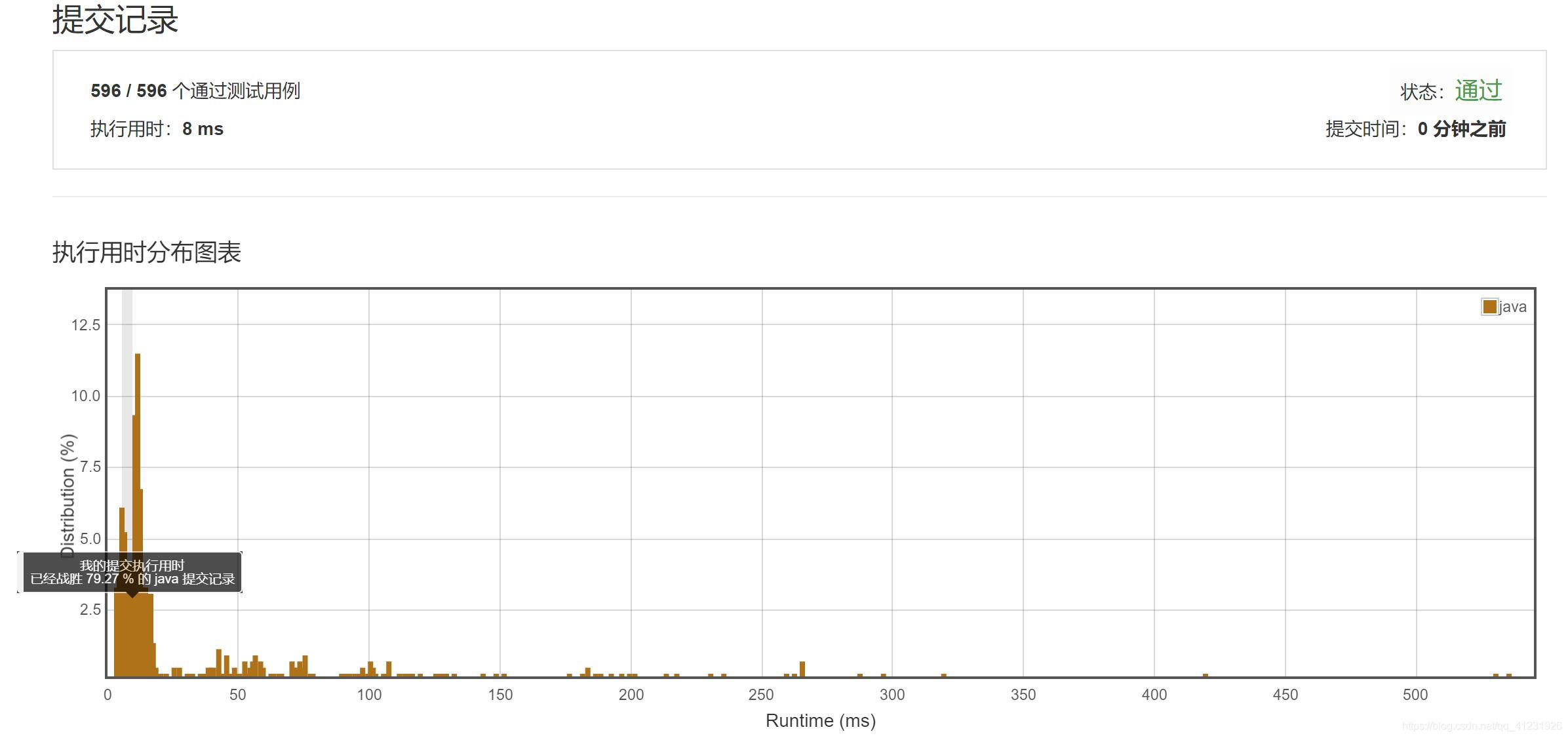
思路四:动态规划
所有的丑数必然在下面3个序列之中:
(1) 1 * 2, 2 * 2, 3 * 2, 4 * 2, 5 * 2, 6 * 2, 7 * 2, ......
(2) 1 * 3, 2 * 3, 3 * 3, 4 * 3, 5 * 3, 6 * 3, 7 * 3, ......
(3) 1 * 5, 2 * 5, 3 * 5, 4 * 5, 5 * 5, 6 * 5, 7 * 5, ......
我们index2、index3和index5这3个指针来标记在上述3个序列中的位置,初始化时这3个指针均为0,表示不包含任何2、3、5,即第一个丑数是1。
而另外3个变量factor2、factor3和factor5分别表示的是当前index2、index3、index5指向的位置的下一个位置,即下一个待选丑数。初始时,由于index2、index3和index5均为0,下一个待选丑数必然是2、3和5。
在for循环中,我们每次取待选丑数中的最小值为第i个丑数。
如果我们选择了factor2的值为第i个丑数,我们需要令index2的值自增1,且factor2的值应该倍更新为第index2(从0开始计数)个丑数的2倍(因为与2相乘的另一个数也必须保证为丑数,而从已经获得的丑数列表里获得的必然是丑数,且index2必然是小于等于i的)。对factor3和factor5做同样的处理。注意,这里不能使用if-else语句,因为factor2、factor3和factor5可能存在相同的情况,这时候都需要更新。
时间复杂度和空间复杂度均为O(n)。
JAVA代码:
//所有的丑数均在下面三组序列中:
// factor1: 1 * 2, 2 * 2, 3 * 2, 4 * 2, 5 * 2, 6 * 2, 7 * 2, ......
// factor2: 1 * 3, 2 * 3, 3 * 3, 4 * 3, 5 * 3, 6 * 3, 7 * 3, ......
// factor3: 1 * 5, 2 * 5, 3 * 5, 4 * 5, 5 * 5, 6 * 5, 7 * 5, ......
public class Solution {
public int nthUglyNumber(int n) {
int[] uglies = new int[n];
uglies[0] = 1; //第一个丑数是1
int index2 = 0, index3 = 0, index5 = 0; //3组序列中3个指针所指向的位置
int factor2 = 2, factor3 = 3, factor5 = 5; //代表3组序列
for (int i = 1; i < n; i++) {
int min = Math.min(Math.min(factor2, factor3), factor5); //在3组序列中选取最小的数
uglies[i] = min;
if (factor2 == min) { //如果选取的是序列factor2
index2++;
factor2 = 2 * uglies[index2]; //更新factor2的值
}
if (factor3 == min) { //如果选取的是序列factor3
index3++;
factor3 = 3 * uglies[index3];
}
if (factor5 == min) { //如果选取的是序列factor5
index5++;
factor5 = 5 * uglies[index5];
}
}
return uglies[n - 1];
}
}
LeetCode解题报告:
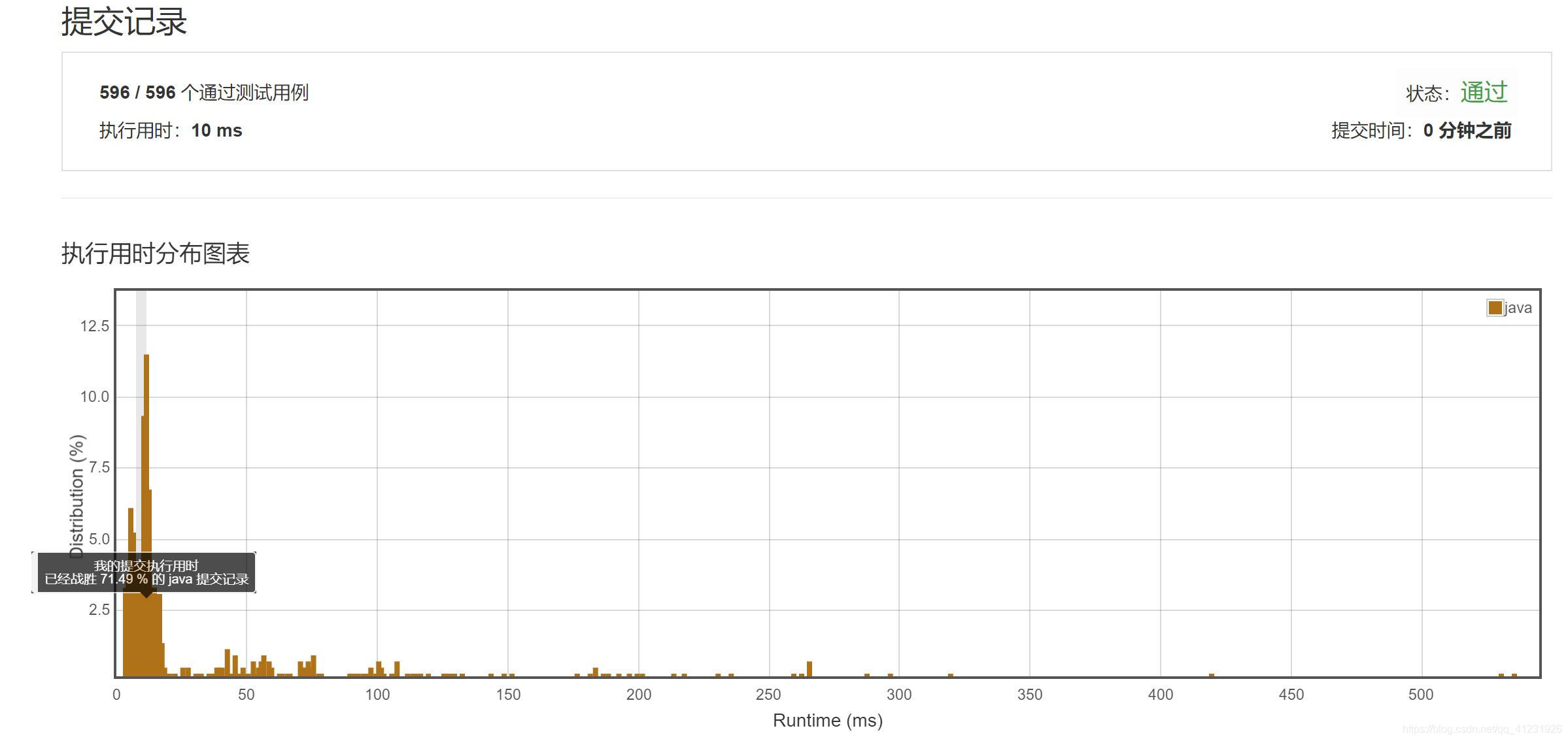





 本文详细解析了LeetCode上“丑数II”问题的四种解法,包括暴力破解法、生成并排序丑数、预处理丑数列表以及动态规划方法。其中,动态规划方法最为高效,通过维护三个指针分别对应2、3、5的倍数序列,逐步生成第n个丑数。
本文详细解析了LeetCode上“丑数II”问题的四种解法,包括暴力破解法、生成并排序丑数、预处理丑数列表以及动态规划方法。其中,动态规划方法最为高效,通过维护三个指针分别对应2、3、5的倍数序列,逐步生成第n个丑数。
















 851
851

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








