LeetCode207——课程表

最新推荐文章于 2024-10-30 12:04:31 发布

原创最新推荐文章于 2024-10-30 12:04:31 发布 · 695 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#LeetCode #Java #Cplusplus #拓扑排序 #课程表

LeetCode题解专栏收录该内容

263 篇文章

订阅专栏

本文探讨了LeetCode上的课程安排问题，通过拓扑排序算法解决课程先修条件问题，详细介绍了算法步骤及JAVA与C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

我的LeetCode代码仓：https://github.com/617076674/LeetCode

原题链接：https://leetcode-cn.com/problems/course-schedule/description/

题目描述：

知识点：拓扑排序

思路：拓扑排序

拓扑排序的算法步骤如下：

（1）定义一个队列Q，并把所有入度为0的节点加入队列。

（2）取队首节点，输出。然后删去所有从它出发的边，并令这些边到达的顶点的入度减1，如果某个顶点的入度减为0，则将其加入队列。

（3）反复进行（2）操作，直到队列为空。如果队列为空时入过队的节点数恰好为N，说明拓扑排序成功，图G为有向无环图；否则，拓扑排序失败，图G中有环。

时间复杂度和空间复杂度均是O(n)。

JAVA代码：

public class Solution {

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int[] inDegree = new int[numCourses];
        int[][] graph = new int[numCourses][numCourses];
        for(int i = 0; i < prerequisites.length; i++){
            graph[prerequisites[i][1]][prerequisites[i][0]] = 1;
            inDegree[prerequisites[i][0]]++;
        }
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 0; i < numCourses; i++){
            if(inDegree[i] == 0){
                queue.add(i);
            }
        }
        int num = 0;
        while(!queue.isEmpty()){
            int u = queue.poll();
            for(int v = 0; v < numCourses; v++){
                if(graph[u][v] != 0){
                    inDegree[v]--;
                    if(inDegree[v] == 0){
                        queue.add(v);
                    }
                }
            }
            num++;
        }
        return num == numCourses;
    }
}

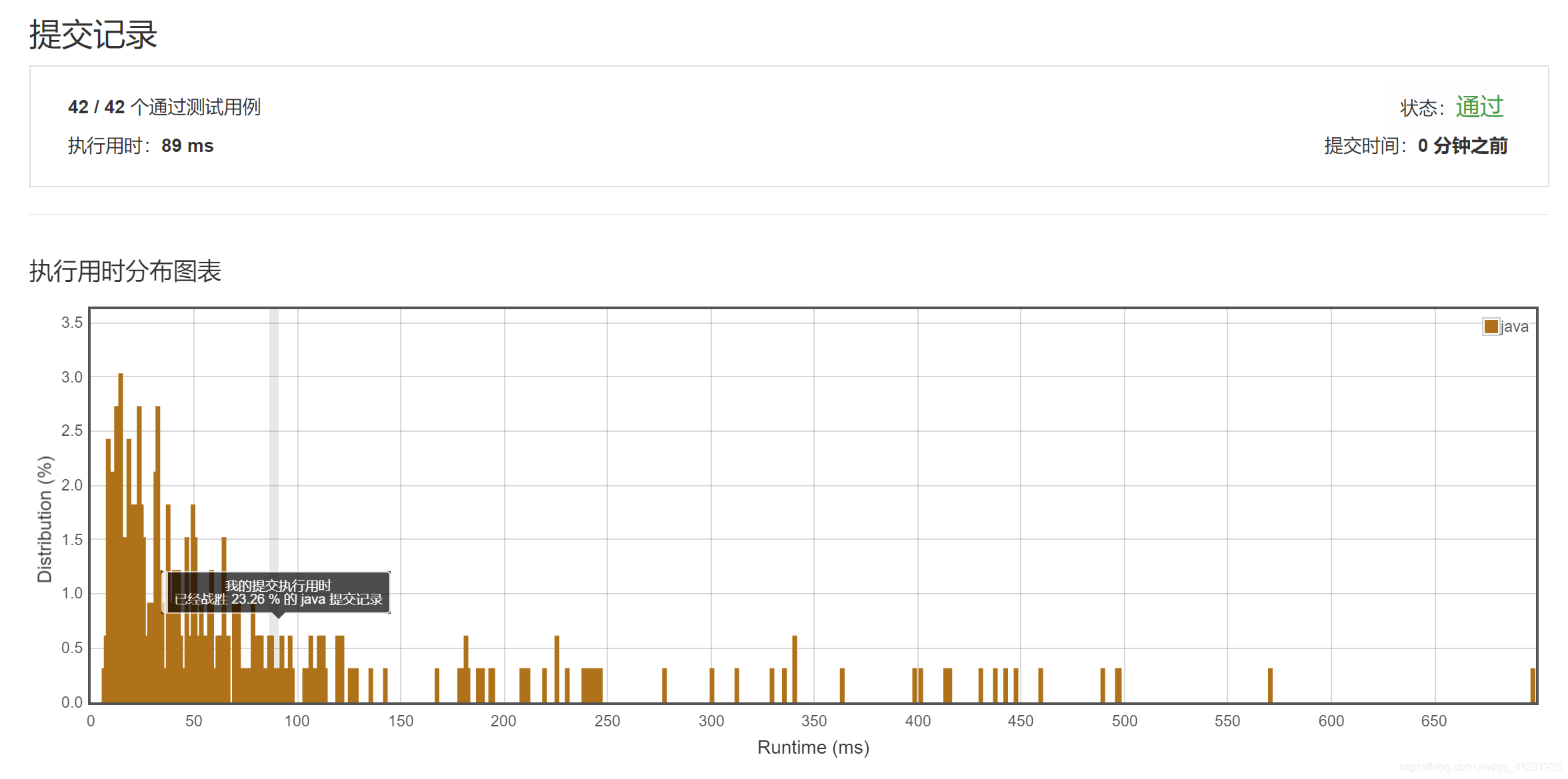
JAVA解题报告：

C++代码：

class Solution {
	public:
		bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
			int inDegree[numCourses] = {0};	//记录每个节点的入度
			vector<int> graph[numCourses];
			for(int i = 0; i < prerequisites.size(); i++) {
				graph[prerequisites[i].second].push_back(prerequisites[i].first);
				inDegree[prerequisites[i].first]++;
			}
			int num = 0;	//记录加入拓扑序列的顶点数
			queue<int> q;
			for(int i = 0; i < numCourses; i++) {
				if(inDegree[i] == 0) {
					q.push(i);	//将所有入度为0的顶点入队
				}
			}
			while(!q.empty()) {
				int u = q.front();	//取队首顶点u
				q.pop();
				for(int i = 0; i < graph[u].size(); i++) {
					int v = graph[u][i];	//u的后继节点v
					inDegree[v]--;	//顶点v的入度减1
					if(inDegree[v] == 0) {
						q.push(v);	//顶点v的入度减为0则入队
					}
				}
//				graph[u].clear(); 
				num++;
			}
			if(num == numCourses){
				return true;	//加入拓扑序列的顶点数为numCourses，说明拓扑排序成功 
			}
			return false;	//加入拓扑序列的顶点数小于numCourses，说明拓扑排序失败 
		}
};

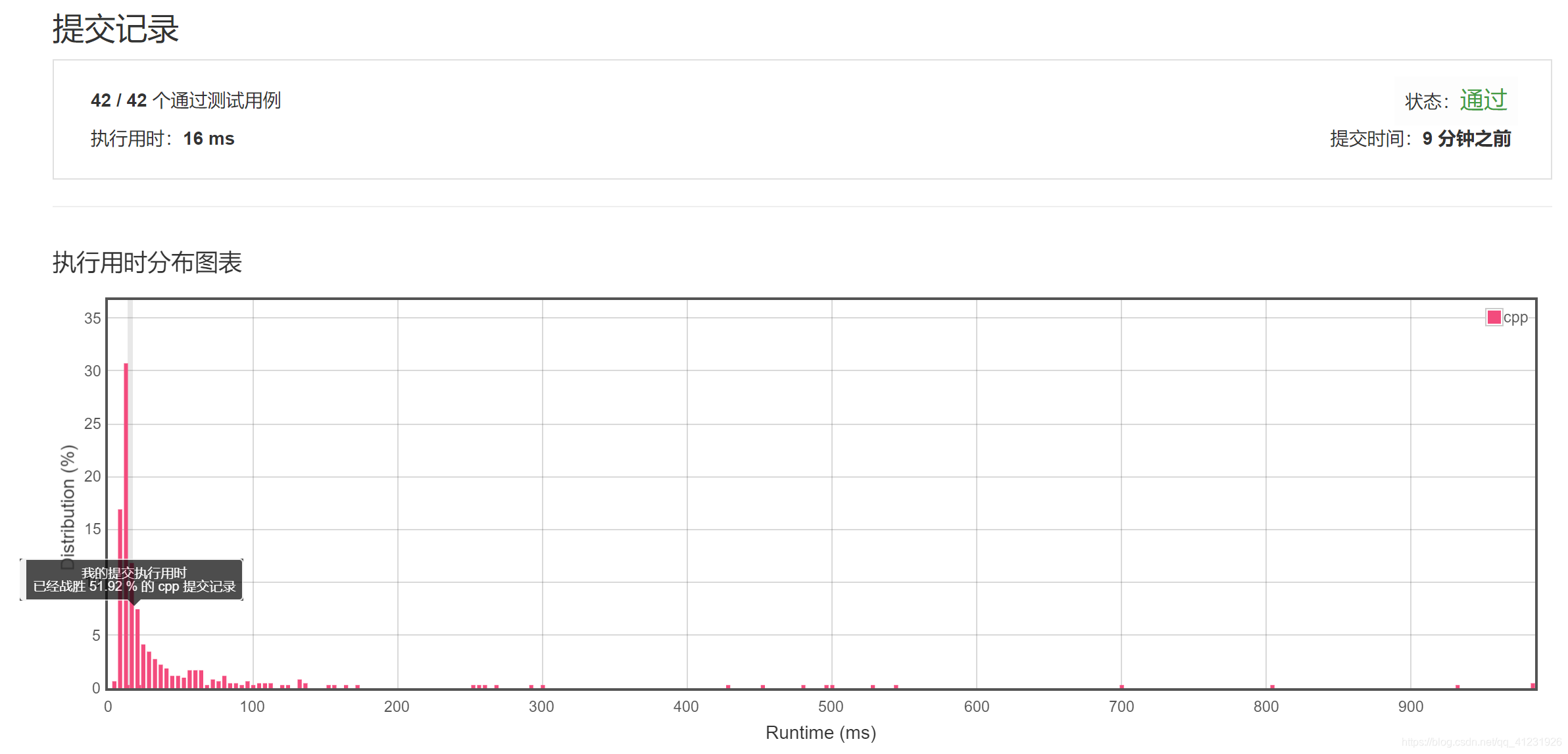
C++解题报告：