SparseArray

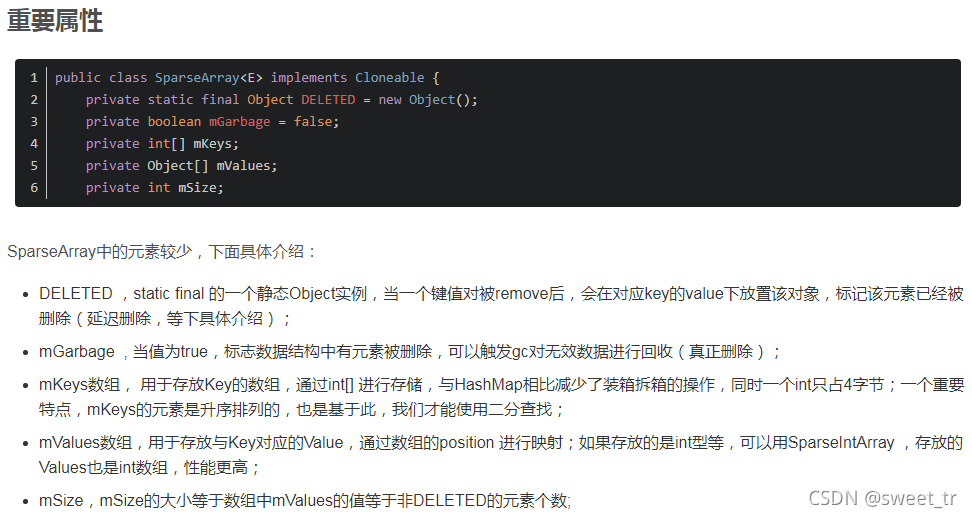
 重点：

1. key是int型的，升序排列

2. 延迟删除机制

3.结构比HashMap简单。（SparseArray内部主要使用两个一维数组来保存数据，一个用来存key，一个用来存value）不需要额外的额外的数据结构，因此能够提高内存效率，但是在时间上的效率不如hashmap，而且不适用于有大量数据的场景。

4.为了提高自身效率，采用二分法的方式进行查找

Android轻量级数据SparseArray详解_楠枫的博客-优快云博客_sparsearray

基本使用

        SparseArray<Object> sparseArray = new SparseArray<>();
        sparseArray.put(0,null);
        sparseArray.put(1,"fsdfd");
        sparseArray.put(2,new String("fjdslfjdk"));
        sparseArray.put(3,1);
        sparseArray.put(4,new Boolean(true));
        sparseArray.put(5,new Object());
        sparseArray.put(8,new String("42fsjfldk"));
        sparseArray.put(20,"jfslfjdkfj");
        sparseArray.put(0,"chongfude");

        int size = sparseArray.size();
        for (int i = 0;i < size;i++) {
            Log.d(TAG, "sparseArraySample: i = " + i + ";value = " + sparseArray.get(sparseArray.keyAt(i)) );
        }

 

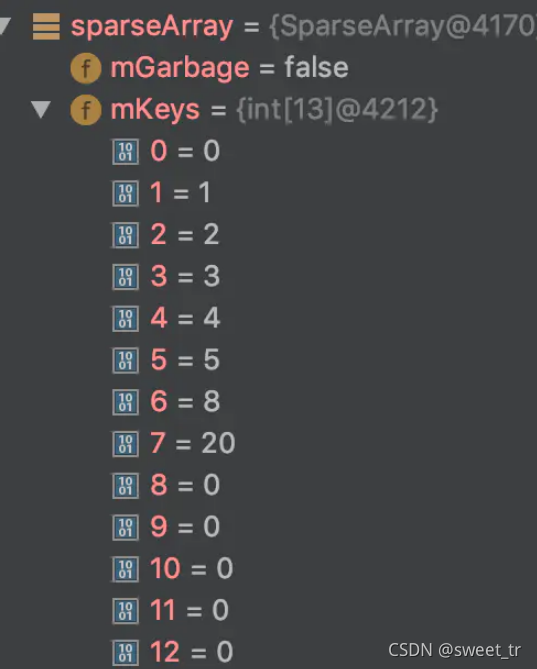
可以看出来， mKeys.length可能会比mSize大。

delete

我们知道研究这种数据结构，肯定是从各种增删查方法入手啦。跟着各位大佬的文章，先看delete方法

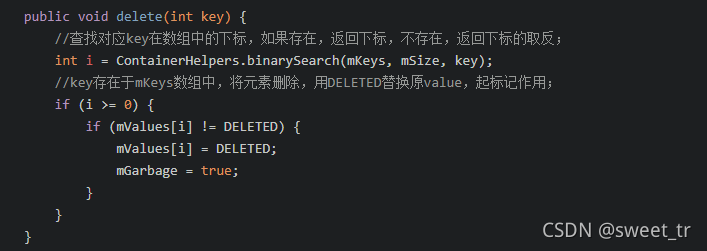 很容易懂，先用二分法在key数组里查找目标key的位置，也就是数组下标，

找到后将原value用DELETE替代，并令mGarbage = true，代表数组中可能存在垃圾

class ContainerHelpers {
 
    // This is Arrays.binarySearch(), but doesn't do any argument validation.
    //第一个参数是keys的数组，第二个为数组中元素个数（与keys的length不一定相等），第三个为目标key
    static int binarySearch(int[] array, int size, int value) {
        //lo为二分查找的左边界
        int lo = 0;
        //hi为二分查找的右边界
        int hi = size - 1;
        //还没找到，继续查找
        while (lo <= hi) {
            //左边界+右边界处以2，获取到mid 的index
            final int mid = (lo + hi) >>> 1;
            //获取中间元素
            final int midVal = array[mid];
            // 目标key在右部分  。。。。感觉这部分太简单了
            if (midVal < value) {
                lo = mid + 1;
            } else if (midVal > value) {
                hi = mid - 1;
            } else {
                //相等，找到了，返回key对应在array的下标；
                return mid;  // value found
            }
        }
        //没有找到该元素，对lo取反！！！！！很重要
        return ~lo;  // value not present
    }

重点：

1. 为什么delete方法最后没有找到不返回-1而是返回一个取反的数？可以看到，返回的这个数是目标key在array的位置下标，或者是应该插入的位置下标的取反

比如一组数：2 4  6 9

目标key是5的话，返回的就是3（下标）的取反。

可以看出来，这样返回对put方法很友好。

2. delete方法最终只是，找到需要删除的key，将对应的value用DELETED替换；但是key仍然存在于mKeys数组，因此删除是一个伪删除。这就是所谓的延迟删除机制。

为什么要有延迟删除呢，感觉可能是因为我们知道数组在put和delete方法上都很麻烦，对应位置后面的数组元素都要变动，如果有延迟删除机制，那么不仅delete方法不需要整体前移，如果在put的时候，对应位置的key保留了，元素就不需要整体后移了，只需要改变对应的value就行了。

put方法

public void put(int key, E value) {
        // 1.先进行二分查找
        int i = ContainerHelpers.binarySearch(mKeys, mSize, key);
        // 2. 如果找到了，则 i 必大于等于 0
        if (i >= 0) {
            mValues[i] = value;
        } else {
        // 3. mKeys里没找到对应的key，所以找一个正确的位置（~i）插入
            i = ~i;
            //如果对应位置的value是DELETE，说明是没来得及回收的，正好可以直接改变value值
            if (i < mSize && mValues[i] == DELETED) {
                mKeys[i] = key;
                mValues[i] = value;
                return;
            }
            //如果有需要回收的并且没空位了，那做一轮回收后重新计算i值
            if (mGarbage && mSize >= mKeys.length) {
                gc();
                // Search again because indices may have changed.
                i = ~ContainerHelpers.binarySearch(mKeys, mSize, key);
            }
            //总归是要插入的，前面的都是特殊情况可以直接替换的，现在才是普通情况，就是需要直接插入的情况
            mKeys = GrowingArrayUtils.insert(mKeys, mSize, i, key);
            mValues = GrowingArrayUtils.insert(mValues, mSize, i, value);
            mSize++;
        }
    }