python进行因子分析（一）

数据来源：https://www.cnblogs.com/wangshanchuan/p/10820326.html，自己把数据写进行了excel，然后用博主的代码一步步实现了下，发现博主的代码出现了一些问题，下面写下分析过程：

import pandas as pd
import numpy as np
import numpy.linalg as nlg
import matplotlib.pyplot as plt
from math import *
from factor_analyzer import *

def main():
    excelFile = 'data.xlsx'
    df=pd.DataFrame(pd.read_excel(excelFile))
    df2=df.copy()
    print("\n原始数据:\n",df2)
    del df2['ID']
    # print(df2)

    # 皮尔森相关系数
    df2_corr=df2.corr()
    print("\n相关系数:\n",df2_corr)

    eig_value, eigvector = nlg.eig(df2_corr)  # 求矩阵R的全部特征值，向量
    eig=sorted(eig_value,reverse=True)        #贡献率排序（从大到小）
    print("\n特征值排序：\n",eig)

这些都没什么问题，接着分析是否可以进行因子分析。

 #热力图
    cmap = cm.Blues
    # cmap = cm.hot_r
    fig=plt.figure()
    ax=fig.add_subplot(111)
    map = ax.imshow(df2_corr, interpolation='nearest', cmap=cmap, vmin=0, vmax=1)
    plt.title('correlation coefficient--headmap')
    ax.set_yticks(range(len(df2_corr.columns)))
    ax.set_yticklabels(df2_corr.columns)
    ax.set_xticks(range(len(df2_corr)))
    ax.set_xticklabels(df2_corr.columns)
    plt.colorbar(map)
    plt.show()

    # KMO测度
    def kmo(dataset_corr):
        corr_inv = np.linalg.inv(dataset_corr)
        nrow_inv_corr, ncol_inv_corr = dataset_corr.shape
        A = np.ones((nrow_inv_corr, ncol_inv_corr))
        for i in range(0, nrow_inv_corr, 1):
            for j in range(i, ncol_inv_corr, 1):
                A[i, j] = -(corr_inv[i, j]) / (math.sqrt(corr_inv[i, i] * corr_inv[j, j]))
                A[j, i] = A[i, j]
        dataset_corr = np.asarray(dataset_corr)
        kmo_num = np.sum(np.square(dataset_corr)) - np.sum(np.square(np.diagonal(A)))
        kmo_denom = kmo_num + np.sum(np.square(A)) - np.sum(np.square(np.diagonal(A)))
        kmo_value = kmo_num / kmo_denom
        return kmo_value

    print("\nKMO测度:", kmo(df2_corr))

    # 巴特利特球形检验
    df2_corr1 = df2_corr.values
    print("\n巴特利特球形检验:", bartlett(df2_corr1[0], df2_corr1[1], df2_corr1[2], df2_corr1[3], df2_corr1[4],
                                  df2_corr1[5], df2_corr1[6], df2_corr1[7], df2_corr1[8], df2_corr1[9],
                                  df2_corr1[10], df2_corr1[11], df2_corr1[12], df2_corr1[13], df2_corr1[14]))

因为不太懂KMO测度和巴特利特球形检验，所以又将数据导入了Spss中进行了因子分析，结果发现两者结果一致。到这一步仍没有什么问题。

怎么求因子载荷矩阵？

将特征向量按照特征值大小依次排序，然后将每列特征向量乘以对应的特征值，即为A。注意这里的特征向量需要经过标准正交化，可以参考之前主成分分析的博文。

    #特征值排序后每个值之前的索引
    index=sorted(range(len(eig_value)), key=lambda k: eig_value[k])

    # 定义单位正交化的函数
    def gram_schmidt(A):
        """Gram-schmidt正交化"""
        global Q    #必须申明为全局变量，否则无法调用Q
        Q=np.zeros_like(A)
        cnt = 0
        for a in A.T:
            u = np.copy(a)
            for i in range(0, cnt):
                u -= np.dot(np.dot(Q[:, i].T, a), Q[:, i]) # 减去待求向量在已求向量上的投影
            e = u / np.linalg.norm(u)  # 归一化
            Q[:, cnt] = e
            cnt += 1
        R = np.dot(Q.T, A)
        print("\n正交单位化后的特征向量：")
        print(Q.T)
    gram_schmidt(eigvector)
    print("\n按特征值大小排列的正交单位化后的特征向量：")

    print(Q.T[index[:]])    #每行是特征向量

另外，要确定公共因子的个数，所以根据特征值来判断累计贡献率达到85%以上，结果为6个，这里选的是排好序后的特征值进行计算。

    #求公因子个数m,使用前m个特征值的比重大于85%的标准，选出了公共因子是六个
    for m in range(1, 15):
        if pd.Series(eig[:m]).sum() / pd.Series(eig).sum() >= 0.85:
            print("\n公因子个数:", m)
            break

于是，只选取前6个特征值及特征向量，按照上面图片公式计算因子载荷矩阵。

    C=B[range(0,6)]
    print(C)

    for i in range(0,6):
        C[i]=C[i]*eig[i]
    C.columns = ['factor1', 'factor2', 'factor3', 'factor4', 'factor5','factor6']
    C.index = df2_corr.columns
    print("\n因子载荷矩阵：\n",C)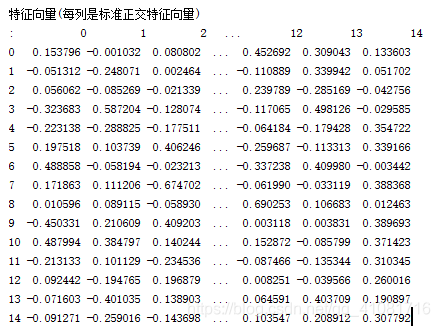

因子载荷矩阵：

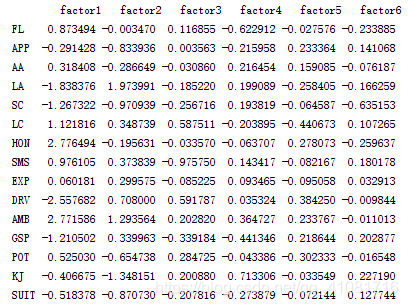
由于因子载荷阵是不唯一的，所以应该对因子载荷阵进行旋转。目的是使因子载荷阵的结构简化，使载荷矩阵每列或行的元素平方值向0和1 两级分化。有三种主要的正交旋转法，四次方最大法、方差最大法和等量最大法。做到这里发现有点看不懂因子旋转，暂时把代码放着吧。因子得分矩阵求取的回归方法https://blog.youkuaiyun.com/qq_29831163/article/details/88915232。

---

在参考了这位老哥的博文后，觉得以后还是要多查看官方文档，不然很多用法不知道。https://blog.youkuaiyun.com/d345389812/article/details/89854792，

还是将结果移到下一篇博文吧，拜拜了！