LeetCode刷题——Day2

4、给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

import java.util.Arrays;
import java.util.Scanner;

public class Day1 {
    
    public static  double findMedianSortedArrays(int[] nums1, int[] nums2) {
         double number=0;
         int[] nums=new int[nums1.length+nums2.length];
         System.arraycopy(nums1,0,nums,0,nums1.length);
         System.arraycopy(nums2,0,nums,nums1.length,nums2.length);//将两个数组复制到一个新数组中，也就是将他们合并
        Arrays.sort(nums);//将合并完的数组排序，方便找中位数
         if(nums.length%2==1)//如果是奇数的话，中位数就是最中间那一个
         {
            number=nums[nums.length/2];
         }
         else
         {
             number=((double)nums[nums.length/2]+(double)nums[nums.length/2-1])/2;//如果是偶数的话，中位数

                                                       就是最中间那两个的平均值
         }
        return number;
            
        }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int nums1[];
        int nums2[];
   Scanner in=new Scanner(System.in);
    int n1=in.nextInt();
     nums1=new int[n1];
    for(int i=0;i<n1;i++)
        nums1[i]=in.nextInt();
    int n2=in.nextInt();
     nums2=new int[n2];
    for(int i=0;i<n2;i++)
        nums2[i]=in.nextInt();
    double number=findMedianSortedArrays(nums1,nums2);
    System.out.println(number);
    }  
}

易错点：1）sort arraycopy函数的语法格式

2）除法的精确度问题，整型除以整型比如5/2即使结果设置为double，我们得到的还是2.0，应该先转为double型

3）java中 静态方法不可以直接调用非静态方法和成员，也不能使用this关键字。因为非静态方法是依赖于对象存在的，也就是说要先实例化一个对象，才可可以使用，所以上面的求中位数函数要用static修饰。

这一题难度显示是困难，我竟然超过84.92%的提交，可是我并没有实现要求的复杂度啊，困惑。

5、给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

反转 SS，使之变成 S'S′。找到 SS 和 S'S′ 之间最长的公共子串，这也必然是最长的回文子串。这种想法有错误：

让我们尝试一下这个例子：S=“abacdfgdcaba” ，S′=“abacdgfdcaba”：

S 以及 S′ 之间的最长公共子串为 “abacd”，显然，这不是回文。我们采用动态规划解决这一题。（下面的做法只超过23%，看来动态规划的时间复杂度还是很高）

思路：考虑 “ababa” 这个示例。如果我们已经知道“bab” 是回文，那么很明显，“ababa” 一定是回文，因为它的左首字母和右尾字母是相同的。

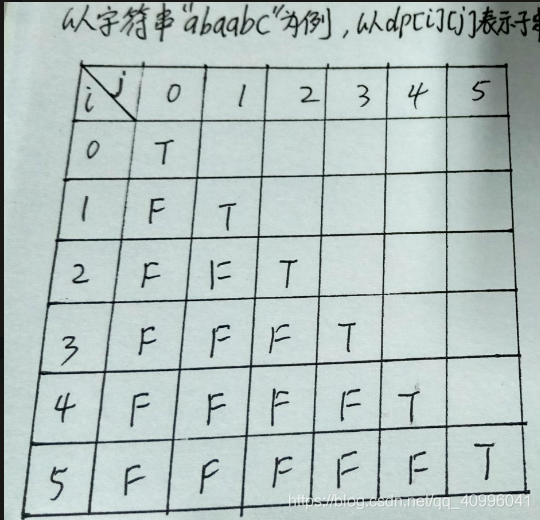
借助一个二维布尔数组：（图来源于网络）

每一个dp[i][j]代表图中一个方格，每个方格中的T和F分别代表当前子串是否为回文字符串，如

dp[1][4]="baab"，由定义,在初始状态可以完全确定图中上三角中方格的值。

补充知识：（1）null与空字符串主要区别如下：

1）null不指向任何对象，相当于没有任何值；而“”代表一个长度为0的字符串

2）null不分配内存空间；而“”会分配内存空间

（2）substring用法

public String substring(int beginIndex, int endIndex)

第一个int为开始的索引，对应String数字中的开始位置，

第二个是截止的索引位置，对应String中的结束位置

1）取得的字符串长度为：endIndex - beginIndex;

2）从beginIndex开始取，到endIndex结束，从0开始数，其中不包括endIndex位置的字符

（3）java中真假的判断不可以if（1），只能是true或false

import java.util.Arrays;
import java.util.Scanner;

public class Day1 {
    public static String longestPalindrome(String s){
        int len=s.length();
        boolean[][] tf=new boolean[len][len];
        String max="";//记录最长子串
        for(int j=0;j<len;j++) {
            for(int i=0;i<=j;i++) {//只需计算矩阵一半即可
                tf[i][j]=(s.charAt(i)==s.charAt(j)&&(j-i<=2||tf[i+1][j-1]));
//重点：tf[i][j]是否为真也就是i到j位置的子串是不是回文子串要经过三个条件的比较
//第一个(s.charAt(i)==s.charAt(j)判断最外层的两个字符是否相等，j-i<=2||tf[i+1][j-1])这两个满足一个即可
//因为如果j-i<=2一定是回文子串，而tf[i+1][j-1])则是体现了这一题动态规划的递推规律
                if(tf[i][j]&&(j-i+1)>max.length()) {
                    max=s.substring(i, j+1);
                }
            }
        }
        
           return max; 
        }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner in=new Scanner(System.in);
        String s=in.next();
        String max=longestPalindrome(s);
        System.out.println(max);
    }
    
}

官方给出的中心扩展算法：

事实上，只需使用恒定的空间，我们就可以在 O(n^2)O(n2) 的时间内解决这个问题。

我们观察到回文中心的两侧互为镜像。因此，回文可以从它的中心展开，并且只有2n−1 个这样的中心，因为所含字母数为偶数的回文的中心可以处于两字母之间。

public String longestPalindrome(String s) {
    if (s == null || s.length() < 1) return "";
    int start = 0, end = 0;
    for (int i = 0; i < s.length(); i++) {
        int len1 = expandAroundCenter(s, i, i);
        int len2 = expandAroundCenter(s, i, i + 1);
        int len = Math.max(len1, len2);
        if (len > end - start) {
            start = i - (len - 1) / 2;
            end = i + len / 2;
        }
    }
    return s.substring(start, end + 1);
}

private int expandAroundCenter(String s, int left, int right) {
    int L = left, R = right;
    while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
        L--;
        R++;
    }
    return R - L - 1;
}