POJ 2385 (DP思想)

Apple Catching

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 14544		Accepted: 7125

Description

It is a little known fact that cows love apples. Farmer John has two apple trees (which are conveniently numbered 1 and 2) in his field, each full of apples. Bessie cannot reach the apples when they are on the tree, so she must wait for them to fall. However, she must catch them in the air since the apples bruise when they hit the ground (and no one wants to eat bruised apples). Bessie is a quick eater, so an apple she does catch is eaten in just a few seconds. 

Each minute, one of the two apple trees drops an apple. Bessie, having much practice, can catch an apple if she is standing under a tree from which one falls. While Bessie can walk between the two trees quickly (in much less than a minute), she can stand under only one tree at any time. Moreover, cows do not get a lot of exercise, so she is not willing to walk back and forth between the trees endlessly (and thus misses some apples). 

Apples fall (one each minute) for T (1 <= T <= 1,000) minutes. Bessie is willing to walk back and forth at most W (1 <= W <= 30) times. Given which tree will drop an apple each minute, determine the maximum number of apples which Bessie can catch. Bessie starts at tree 1.

Input

* Line 1: Two space separated integers: T and W 

* Lines 2..T+1: 1 or 2: the tree that will drop an apple each minute.

Output

* Line 1: The maximum number of apples Bessie can catch without walking more than W times.

Sample Input

7 2
2
1
1
2
2
1
1

Sample Output

6

Hint

INPUT DETAILS: 

Seven apples fall - one from tree 2, then two in a row from tree 1, then two in a row from tree 2, then two in a row from tree 1. Bessie is willing to walk from one tree to the other twice. 

OUTPUT DETAILS: 

Bessie can catch six apples by staying under tree 1 until the first two have dropped, then moving to tree 2 for the next two, then returning back to tree 1 for the final two.

Source

USACO 2004 November

很好的一道DP题。感谢大佬提供的思路      大佬思路

思路：

        在这道题中奶牛是可以移动w步的，而且它面前只有两棵树，我刚开始是用递归做的。（一直超时，从不停歇）。

        其实，在递归超时之后。大家就应该想到用递推来做。（DP不容易想，需要多加思考）

        那么，在这道题中，我们可以这样想一下。奶牛移动之后面对的只有两棵树。那么，我们的移动步数和这两棵树之间是否有一些关系呢。说到这，我们就很容易想到（令j为步数）  则j%2+1  就可以很好的理解为奶牛现在所面对的树。

        那么我们就可以判断奶牛此时面对的树与题目给定的掉落苹果的树之间的关系--->flag = (j%2+1 == a[i]).

        dp[i][j]数组为奶牛移动步数之后能得到的苹果树  其中i为秒数 j为步数

         所以，由上边我们就可以得知：

            当flag为true时我们的dp[i][j] = max(dp[i-1][j-1],dp[i-1][j])+1;

            反之 dp[i][j] = max(dp[i-1][j-1],dp[i-1][j]);

    代码如下

      

附一张样例dp数组截图  可以好好参照理解一下

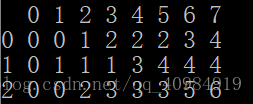
#include<map>
#include<stack>
#include<math.h>
#include<string>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define pi acos(-1)
using namespace std;
typedef long long ll;
const int MAX_N=100000+50;
const int INF=0x3f3f3f3f;

int dp[1010][1010];
int a[MAX_N];

int main()
{
 	int t,w; 
 	while(cin>>t>>w)
 	{
 		memset(dp,0,sizeof(dp));
 		for(int i = 1; i <= t; i++)
		{
		 	cin>>a[i];
		}
		
		for(int i = 1; i <= t; i++)
		{    
        	dp[i][0] = dp[i-1][0];   
            if(a[i] == 1)    
                dp[i][0]++;    
            for(int j = 1;j <= w; j++)
			{    
                if(j % 2 + 1 == a[i])
				{    
                    dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + 1;    
                }    
                else    
                    dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]);    
            }    
        }   
		int maxv=0;
		for(int i = 0; i <= w ; i++)
		{
			maxv = max(maxv,dp[t][i]);
		}
		cout<<maxv<<endl;
	}
	return 0;
}