SVM与硬/软间隔

• SVM/支持向量机

• SVM Hard Margin

• SVM Soft Margin

SVM支持向量机

在神经网络尚未得到广泛的关注与应用之前，在分类与回归问题上，SVM当仁不让的王者。其核心思想就是分为了输入空间与特征空间两个不同的空间。输入空间一般为欧式空间或者离散集合,特征空间是欧式空间或者希尔伯特空间。支持向量机假设二者之间存在一个相互映射的关系，可以通过一种线性或者非线性的方式将输入空间数据映射到特征空间，成为相应的特征向量，因此支持向量机学习的是特征空间中的特征，在特征空间上进行学习的。

支持向量机的求解实际上是一个凸优化的问题，求解目标可以概括为：寻找一条线或者一个面，使得距离该边界最近的点之间能够距离最远，句子比较拗口，下面以一幅图展示一下

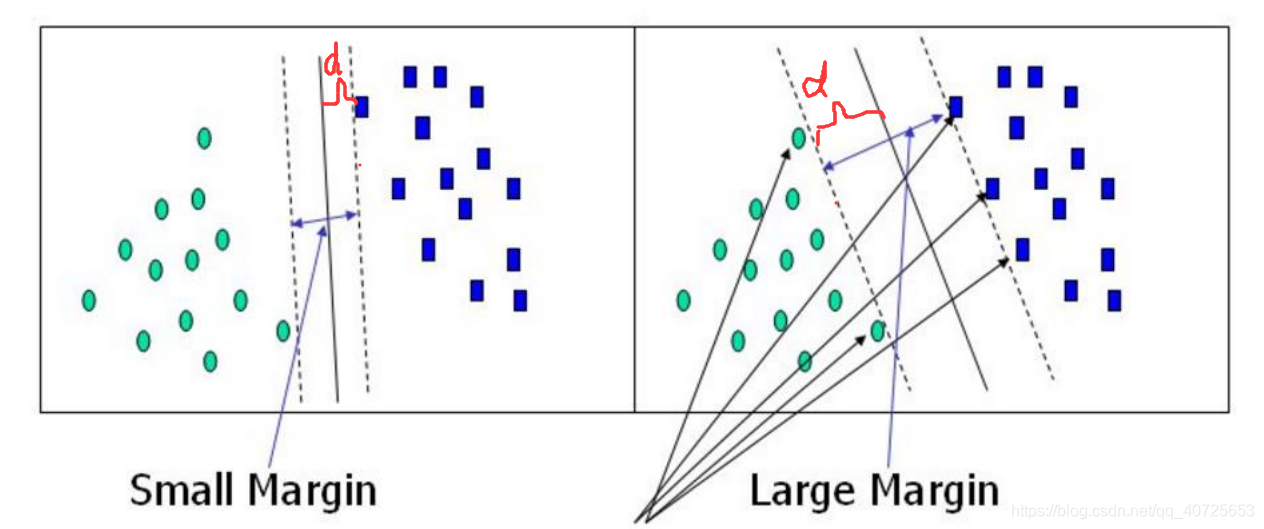
如上图所以，一个简单二分类问题，我们能够找到N中分割方式，能够将二者完美的分割开来，我们的目的是寻找一条最为合适的分界面能够使我们的分类效果很好。上面紫色的那句话在图中就是我用红色d表示的区域，我们致力于寻找最大的d(打个比方，两边陷阱很多，我们人数有很多，我们只能尽可能从两种陷阱中寻求一条最宽的路进而快速通过且安全)
那么如何求取这个maxd则成为了我们关注的核心问题，由此引入了下面两种方式

SVM Hard Margin

如上图所示，我们要求maxd，首先我们要先求得d的表示形式

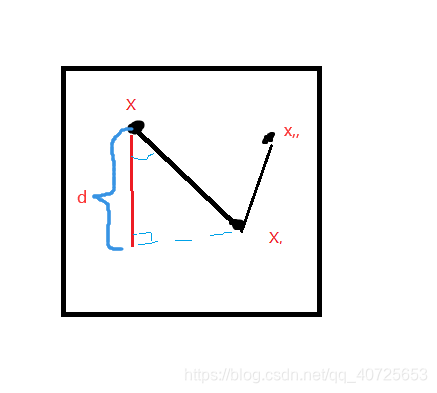
假设x,与x,为平面上的两个点，x为特征空间上一个点，则图中距离distance为：
$d=|w^T/||w||(x-x,)|$,其中w为面的法向量，除以||w||使之成为单位法向向量，（x-x,）为xx,的方向向量，最终二者的点积可以得到d的距离。

这样一个超平面或者线可以表示为:
$wx+b=0$
最终分类函数可以表示为
$f(x)=sign(wx+b)$

目前为止我们关键问题就转化为如何求未知数w与b得到我们相应的分界面表达式及其最后的分类函数
$y_i=w{x}_i+b=0$
然后我们对d进行化简
$d=|w^T/||w||(x-x,)|=1/||w||(|w^{T}x-w^{T}x,|)=1/||w||(|w^{T}x+b|)$

针对这样一个分类问题，我们可以进行一个缩放，我们将正类分为+1，负类分为-1(这里不管什么情况你总能缩放为1，当然也可以为其他任意值，1为了后续推导方便)
$y_i=w{x}_i+b=1$
$y_i=w{x}_i+b=-1$

上述有个明显的问题就是不能随意去绝对值，里面存在符号问题，这里我们采用$y_i$取代||，因为$y_i与wx+b$相乘为1，等价于去掉绝对值
$d=|w^T/||w||(x-x,)|=1/||w||(|w^{T}x-w^{T}x,|)=1/||w||(|w^T+b|)=1/||w||y_i(wx+b)=1/||w||$

最上面图可知，d为其间隔的一般，呈现对称性，因此实际距离$d=2/||w||$
至此，我们目标再一次变化转换为求$max(2/||w||)$,且含有$y_i(w{x}_i+b)\ge 1$的约束
一般情况下我们都会将求极大转化为求极小值进行优化，上述等价于$min||w|{|}^2/2$,且含有$y_i(w{x}_i+b)\ge 1$的约束

求最优解和约束条件，是不是想到了拉格朗日乘子，这里建议忘记拉格朗日乘子的话一定先点击这里(Lagrange)简单看一看，了解下拉格朗日乘子法与对偶问题以及KKT条件

目标函数：$min||w|{|}^2/2$
   st : $y_i(wx+b)\ge 1$
应用拉格朗日乘子法：
$L(x,b,\alpha )=||w|{|}^2/2-{\sum }_i^m{\alpha }_i(y_i(wx+b)-1)$
利用其强对偶性质，将其转化为无条件的对偶问题
$$maxL(w,b,\alpha )=\{\begin{array}{rlr}{f}_0(w)& & \text{满足约束时}\\ +\infty & & \text{else}\end{array}$$
$mi{n}_{w,b}(ma{x}_{\alpha }(L(w,b,\alpha )))=ma{x}_{\alpha }(mi{n}_{w,b}(L(w,b,\alpha )))$此处不清楚的，强烈安利点击上面蓝色字体
首先对w,b进行求导
${▽}_{w}L(x,b,\alpha )=0推出w={\sum }_i^m{\alpha }_i{y}_i{x}_i$
${▽}_{b}L(x,b,\alpha )=0推出0={\sum }_i^m{\alpha }_i{y}_i$
将上述两式带入到L中：
$L(x,b,\alpha )={\sum }_i^m{\alpha }_i-1/2{\sum }_i^m{\sum }_j^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j$其中$x_i,x_j$内积形式相乘得到一个标量
然后在针对L求$\alpha$的最优解，$ma{x}_{\alpha }L(\alpha )$,约束为${\alpha }_i\ge 0，y_i(wx+b)\ge 1$，求出$\alpha$后代入上述推导式得到最终的分界面为：
$0=w{x}_i+b={\sum }_i^m{\alpha }_i{y}_i{x}_{i}x+b$ ,其中b可由$\alpha$代入得出
分类函数为：
$f(x)=sign(wx+b)=sign({\sum }_i^m{\alpha }_i{y}_i{x}_{i}x+b)$

为什么叫做支持向量机呢？
求解上述的α,就会惊奇的发现，α只在其边界处有值且≠0，而其余部分点的α全部为0.因此在最终的决策线或面中只有α≠0的发挥了
作用，如第一幅图边界上的向量在分类中起到了分类作用，这些向量称之为支持向量(蓝色方框)。因此该分类方法称之为支持向量机。
如下图所示

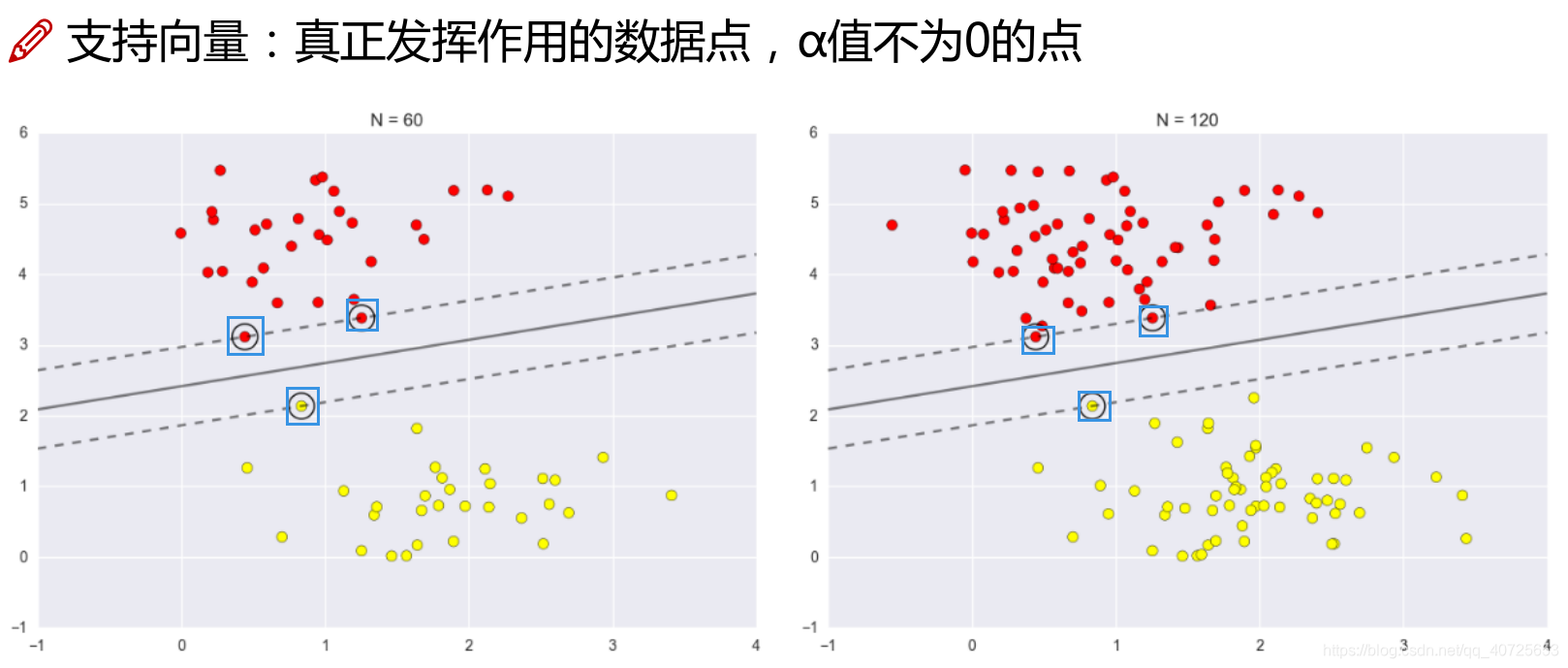
SVM Soft Margin

上述的理想线性分类方式在实际应用中会受到诸多严峻的挑战，如噪音的影响。由于噪音的存在可能使一部分的点不满足我们的约束条件，进而会造成最终的分类效果较差。为应对此种现象，又提出了软间隔方法，方法便是在原有目标的基础上添加一个loss函数，将原有的硬划分改变为一种软分类的思想。我们事先就允许它有一定的错误

我们将hard margin中改为：
目标函数：$min||w|{|}^2/2+loss$
   st : 损失函数loss的约束

至此我们现今目标为研究什么样的loss作为损失函数合适？
首先考虑常见的0/1损失：
$$loss=\{\begin{array}{rlr}0& & \text{yi(wx+b)≥1}\\ 1& & \text{else}\end{array}$$
显然，该函数呈现跳跃性，不连续、不可导数学性质不好，因此不适用
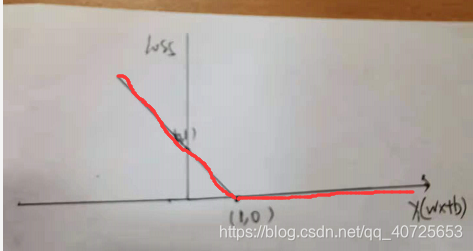
其次我们在考虑一种以距离远近形式定义的损失，又称之为合页损失函数

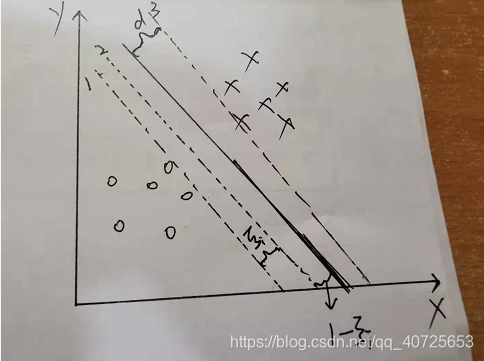
其思想如上图所示，我们允许边界约束条件有一个${\xi }_i$的浮动范围，原本的约束$y_i(wx+b)\ge 1$则变为了2号虚线所示的$y_i(wx+b)\ge 1-{\xi }_i$,其loss为：
$$loss=\{\begin{array}{rlr}0& & \text{yi(wx+b)≥1}\\ y_i(wx+b)& & \text{else}\end{array}$$

由此，目标函数，约束变为：
目标函数：$min||w|{|}^2/2+C{\sum }_i^m{\xi }_i$
   st : $y_i(wx+b)\ge 1-{\xi }_i$
   st : ${\xi }_i\ge 0$
我允许你有些点不满足我原有的约束，我通过你不满足的程度来添加不同程度的损失，相当于添加了一个惩罚系数。你越不满足我条件，给与你损失越大，惩罚越大

应用拉格朗日乘子法：
$L(x,b,\xi ,\alpha )=||w|{|}^2/2+C{\sum }_i^N{\xi }_i-{\sum }_i^m{\alpha }_i(y_i(wx+b)-1+{\xi }_i)$
下面操作同hard margin一致
对$w,b,\xi$求导
${▽}_{w}L(x,b,\xi ,\alpha )=0推出w={\sum }_i^m{\alpha }_i{y}_i{x}_i$
${▽}_{b}L(x,b,\xi ,\alpha )=0推出0={\sum }_i^m{\alpha }_i{y}_i$
${▽}_{\xi }L(x,b,\xi ,\alpha )=0推出C={\alpha }_i$

将上述三式代入L
$L(x,b,\xi ,\alpha )=||w|{|}^2/2+C{\sum }_i^N{\xi }_i-{\sum }_i^m{\alpha }_i(y_i(wx+b)-1+{\xi }_i)={\sum }_i^m{\alpha }_i-1/2{\sum }_i^m{\sum }_j^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j$
后面操作同上述一样

小结

SVM理论流程：
1：将带约束的凸优化问题利用拉格朗日乘子法转换为无约束的优化问题
2：将无约束的优化问题转换成对偶问题
3：利用对偶问题实现最小最大与最大最小之间的转换(需要KKT条件或slater条件)SVM天生满足强对偶性
4：软间隔中添加一种损失，给与边界决策时一定的浮动

下一篇，SVM之核技巧