Chapter2 Vector Spaces

Chapter2 Vector Spaces

2.1 Vector Spaces and Subspaces

A real vector space is a set of vectors together with rules for vector addition and multiplication by real numbers.

A vector space need to satisfy eight rules

Definition. A subspace of a vector space is a nonempty subset that satifies the requirements for a vector spaces: Linear combination stay in the subspace.

​ (1) if we add any vector $x$ and $y$ in the subspace, $x+y$ is in the subspace;

​ (2) if we multiply and vector $x$ in the subspace by any scalar $c$, $cx$ is in the subspace.

The Column Space of $A$

The column space contains all linear combinations of the columns of $A$. It is subspace of $R^m$.

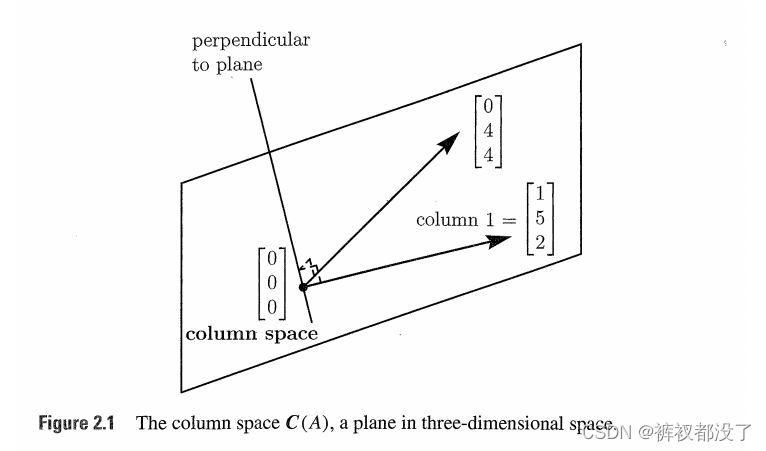
2A The system $Ax=b$ is solvable if and only if the vector $b$ can be expressed as a combination of the columns of $A$. Then $b$ is in the column space.

we can describe all combinations of the two columns geometrically: $Ax=b$ can be solved if and only if $b$ lies in the planes that is spanned by the two column vectors(Figure 2.1).

The Nullspace of $A$

For $Ax=b$, we are concerned not only with attainable right-hand sides $b$, but also with the solutions $x$ that attain them. The solutions to $Ax=0$ form a vector space – the nullspace of $A$.

The nullspace of a matrix consists of all vectors $x$ such that $Ax=0$. It is denoted by $N(A)$. It is a subspace of $R^n$, just as the column space was a subspace of $R^m$.

We want to be able, for any $Ax=b$, to find $C(A)$ and $N(A)$: all attainable right-hand sides $b$ and all solutions to $Ax=0$.

The vectors $b$ are in the column space and the vector $x$ are in the nullspace.

2.2 Solving $Ax=0$ and $Ax=b$

When the nullspace contains more than the zero vector and/or the column space contains less than all vectors:

1. Any vector $x_n$ in the nullspcae can be added to a particular solution $x_p$. The solutions to all linear equations have this form, $x=x_p+x_n$:

   ​ Complete solution $A{x}_p=b$ and $A{x}_n=0$ produce $A(x_p+x_n)=b$

2. When the column space doesn’t contain every $b$ in $R^m$, we need the conditions on $b$ that make $Ax=b$ solvable.

Echelon Form $U$ and Row Reduced Form $R$

$$\text{Basic}\text{Example}:A=\left[\begin{array}{cccc}1& 3& 3& 2\\ 2& 6& 9& 7\\ -1& -3& 3& 4\end{array}\right]$$

$$\text{Echelon}\text{matrix}:U=\left[\begin{array}{cccc}1& 3& 3& 2\\ 0& 0& 3& 3\\ 0& 0& 0& 0\end{array}\right]$$

There extern a lower triangular matrix $L$, make $A=LU$
$$\text{Lower}\text{triangular}:L=\left[\begin{array}{ccc}1& 0& 0\\ 2& 1& 0\\ -1& 2& 1\end{array}\right]andA=LU$$
2B For any $m$ by $n$ matrix $A$ there is a permutation $P$, a lower triangular $L$ with unit diagonal, and an $m$ by $n$ echelon matrix $U$, such that $PA=LU$.
$$\text{Row Reduced}\text{Form}:R=\left[\begin{array}{cccc}1& 3& 0& -1\\ 0& 0& 1& 1\\ 0& 0& 0& 0\end{array}\right]$$
The matrix $R$ is the final result of elimination on $A$. From $R$ we will quickly find the nullspace of $A$. $Rx=0$ has the same solutions as $Ux=0$ and $Ax=0$.

Pivot Variables and Free Variables

$$\text{Nullspace of }R\text{ (pivot columns in boldface)}:R=\left[\begin{array}{cccc}1& 3& 0& -1\\ 0& 0& 1& 1\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}u\\ v\\ w\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$$

The unknowns $u,v,w,y$ go into two groups. One group contains the pivot variables, those that correspond to columns with pivots, The other group is made up of the free variables, corresponding to cloums without pivots.

To find the most general solution to $Rx=0$ we may assign arbitrary values to the free variables. The pivot variables are completely determined in terms of $v$ and $y$.
$$Rx=0-->\begin{array}{c}u+x-y=0\\ w+y=0\end{array}-->\begin{array}{c}u=-3v+y\\ w=-y\end{array}\text{\hspace{1em}(1)}$$
look again at this complete solution to $Rx = 0 $ and $Ax=0$. The first special solution $(-3,1,0,0)$ has free variables $v=1,y=0$. The other special solution $(1,0,-1,-1)$ has $v=0$ and $y=1$. All solutions are linear combinations of these two.
$$\text{Nullspace contians all combinations of special solutions}:x=\left[\begin{array}{c}-3v+y\\ v\\ -y\\ y\end{array}\right]=v\left[\begin{array}{c}-3\\ 1\\ 0\\ 0\end{array}\right]+y\left[\begin{array}{c}1\\ 0\\ -1\\ 1\end{array}\right]$$
The Nullspace matrix as follow:
$$\text{Nullspace matrix (columns are special solutions)}:N=\left[\begin{array}{cc}-3& 1\\ 1& 0\\ 0& -1\\ 0& 1\end{array}\right]$$
2C If $Ax=0$ has more unknowns than equations(n > m), it has at least one special solution: There are more solutions than the trivial $x=0$

The nullspace has the same “dimension” as the number of free variables and special solutions.

Solving $Ax=b,Ux=c$ and $Rx=d $

For the original example $Ax=b=(b_1,b_2,b_3)=(1,5,5)$, apply to both sides the operations that led from $A$ to $U$, The result is an upper triangular systems $Ux=c$:
$$Ux=c\left[\begin{array}{cccc}1& 3& 3& 2\\ 0& 0& 3& 3\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}u\\ v\\ w\\ y\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2-2b_1\\ b_3-2b_2+5b_1\end{array}\right]$$
Every solution to $Ax=b$ is the sum of one particular solution and a solution to $Ax=0$ :
$$x_{complete}=x_{particular}+x_{nullspace}$$
The particular solution comes from solving the equation with all free virables set to zero.

Question: How does the reduced form $R$ make this solution even clearer?
$$Rx=d\left[\begin{array}{cccc}1& 3& 0& 1\\ 0& 0& 1& 1\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}u\\ v\\ w\\ y\end{array}\right]=\left[\begin{array}{c}-2\\ 1\\ 0\end{array}\right]$$
The entries of $d$ go directly into $x_p$.

2D Suppose elimination reduces $Ax=b$ to $Ux=c$ and $Rx=d$, with $r$ pivot rows and $r$ pivot columns. The rank of those matrices is $r$. The last $m-r$ rows of $U$ and $R$ are zero, so there is a solution only if the last $m-r$ entries of $c$ and $d$ are also zero.

2.3 Linear Independence, Basis, and Dimension

Linear Independece

2E Suppose $c_1{v}_1+\cdots +c_k{v}_k=0$ only happens when $c_1=\cdots =c_k=0$. Then the vectors $v_1,\dots ,v_k$ are linearly independent. If any $c$'s are nonzero, the $v$'s are linearly dependent. One vector is a combination of the others.

The columns of $A$ are independent exactly when N(A)={zero vector}N(A) = \{zero\ vector\}N(A)={zero vector}

The $r$ nonzero rows of an echelon matrix $U$ and a reduced matrix $R$ are linearly independent. So are the $r$ columns that contain pivots

Every system $Ac=0$ with more unknowns than equations has solution $c\ne 0$

Spanning a Subspace

2H If a vector space $V$ consists of all linear combinations of $w_1,\dots w_l$, then these vectors span the space. Every vector $v$ in $V$ is the combination of the $w$'s:

​ Every $v$ comes from $w$'s $v=c_1{w}_1+\cdots +c_l{w}_l$ for some coefficients $c_i$.

Basis for a Vector Space

Spanning involves the column space, and independence involoves the nullspace

2I A basis for $V$ is a sequence of vectors having two properties at once:

1. The vectors are linearly independent (not too many vectors)
2. **They span the space $V$ (not too few vectors) **

Dimension of a Vector Space

**The number of basis vector is a property of the space itself : **

2J Any two bases for a vector space $V$ contains same number of vectors. This number, which is shared by all bases and expresses the number of “degree of freedom” of the space, is the dimension of $V$.

The dimension of a space is the number of vectors in every basis.

A basis is a maximal independent set. A basis is also a minimal spanning set.

The notation “dimension” : We speak about a four-dimensional vector, meaning a vector in $R^4$. Now we have defined a four-dimensional subspace; an example is the set of vectors in $R^6$ whose first and last components are zero.
$$\begin{gathered} rank(A)=\#\text{piovt colums}=\text{ dimension of column space} \\ dimension(N(A))=\#\text{free variables}=n-r \end{gathered}$$

2.4 The Four Fundamental Subspaces

Subspace can be described in two ways. First, we may give a set of vectors that span the space. Second, we may told which conditions the vectors in the space must satisfy. (Example: The nullspace consists of all vectors that satisfy $Ax=0$)

When the rank is as large as possible, $r=n$ or $r=m$ or $r=n=m$, the matrix has a left-inverse $B$ or a right-inverse $C$ or a two-sided $A^{-1}$.

The following introduce four subspaces:

1. The column subspace of $A$ is denoted by $C(A)$. Its dimension is the rank $r$.
2. The nullspace of $A$ is denoted by $N(A)$. Its dimension is $n-r$.
3. The row space of $A$ is the column space of $A^T$. It is $C(A^T)$, and it is spanned by the rows of $A$. Its dimension is the rank r.
4. The left nullspace of $A$ is the nullspace of $A^T$. It contains all vectors $y$ such that $A^Ty =0 $, and it is written $N(A^T)$. Its dimension is $m-r$.

The nullspace of $A$ and row space $C(A^T)$ are subspace of $R^n$.

The left nullspace $N(A^T)$ and column space $C(A)$ are subspace of $R^n$

3 The row space of $A$

**2M The row space of $A$ has the same dimension $r$ as the row space of $U$, and it has the same bases, because the row spaces of $A$ and $U$(and $R$) are the same **

2 The nullspace of $A$

2N The nullspace $N(A)$ has dimension $n-r$. The “special solutions” are a basis-- each free variable is given the value 1, while the other free vaiables are 0. The $Ax=0$ or $Ux=0$ or $Rx=0$ gives the pivot variables by back-substitution.

The nullspace is also called the kernel of $A$, and its dimension $n-r$ is the nullity.

1 The column space of $A$

2O The dimension of the column space $C(A)$ equals the rank $r$, which also equals the dimension of the row space: The number of independent columns equals the number of independent rows. A basis for $C(A)$ is formed by the $r$ columns of $A$ that correspond, in $U$, to the columns containing pivots.

4 The left nullspace of $A$ (= nullspace of $A^T$)

2P The left nullspace $N(A^T)$ has dimension $m-r$

Existence of inverses

We want to prove that when $r=m$ there is a right-inverse, and $Ax=b$ always has a solutioin. When $r=n$ there is a left-inverse, and the solution(if it exists) is unique.