机器学习实战（十）：Introduction to Artificial Neural Networks

From Biological to Artificial Neurons

生物元这里就不介绍了，主要说下逻辑神经元计算。

Logical Computations with Neurons

人工神经元：有一个或多个二进制输入和一个二进制输出。一定数量的输入都是激活状态时，人工神经元就会激活输出。

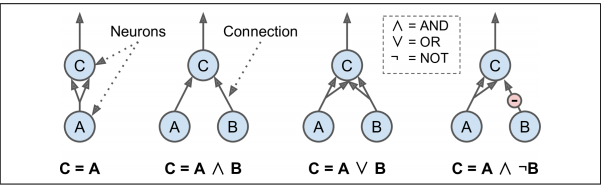
如图所示的四种计算，一个神经元至少两个输入被激活时，自身便处于激活状态。

1. 等同函数：A是激活的，C是激活的，A是非激活的，C也非激活
2. 逻辑与：AB都激活，C激活
3. 逻辑或：AB中有一激活，C激活
4. A激活，B非激活，C激活

The Perceptron（感知器）

感知器是最简单的ANN架构之一，基于线性阈值单元（LTU）人工神经元构成
输入输出都是数字，每个输入都有对应权重，LTU加权输出（z = w1 x1+w2 x2+ ⋯ + wn xn = wT· x），对求职结果用阶跃函数输出，如图所示。

感知器最常见的阶跃函数为Heaviside阶跃函数或符号函数：

单个LTU可做简单线性二值分类：大于阈值为正，小于阈值为负，若用LTU训练花瓣长宽分类鸢尾花，则目标为寻找w0,w1,w2正确值。

感知器就是单个LTU，每个神经元与所有输入相连，通常用特殊神经元传递（输入=输出），再加一个额外偏差（x0 = 1）。偏差特征用偏差神经元表示，永远输出1.

如图展示一个两个输入是三个输出，可以将实例分为三个不同二进制类，被称为多输出分类器。

感知器训练过程利用Hebb定律（当两个神经元有相同输出时，连接权重增强）变体训练，考虑网络错误，导致错误输出连接不增强权重，即满足下列公式：

• w_i_j:第i个输入神经元和第j个输出神经元连接权重
• x_i:训练实例第i个输入值
• y_j_hat:当前训练实例第j个神经元输出
• y_jd:当前训练实例第j个神经元目标输出
• yta:学习率

每个输出神经元决策边界都为线性，即使感知器无法学习复杂模式。感知器收敛定理证明：若训练实例线性可分，则此算法一定会收敛到一个解。

Scikit-Learn提供实现单一LTU网络的Perceptron类：在鸢尾花集上工作：

#Perceptrons max_设置iter 和 tol可以避免Scikit-Learn版本默认警告
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron

iris = load_iris()
X = iris.data[:, (2, 3)]  # petal length, petal width
y = (iris.target == 0).astype(np.int)

per_clf = Perceptron(max_iter=100, tol=-np.infty, random_state=42)
per_clf.fit(X, y)

y_pred = per_clf.predict([[2, 0.5]])

感知器学习算法酷似随机梯度下降法，等同于以下超参数：SGDClassifier: loss=“perceptron”,
learning_rate=“constant”, eta0=1 (the learning rate), and penalty=None

与逻辑回归分类器相反，感知器不输出某个概率而是根据固定值做预测（所以更应该使用逻辑回归）。

感知器也有一系列问题，如异或分类问题（XOR）。但通过感知器堆叠可以消除一部分——多层感知器（MLP）.

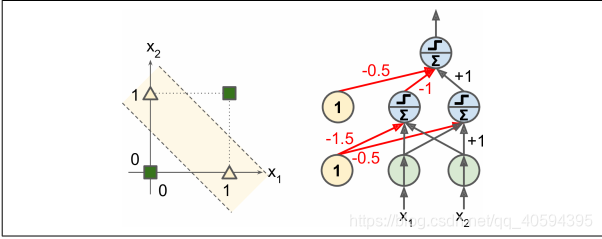
上例中(0,0)、(1,1)输出0，(0,1)产生1.

Multi-Layer Perceptron and Backpropagation(多层感知器和反向传播 )

MLP组成：

• 一个（透传）输入层
• 一个或多个隐藏层的LTU层
• 一个输出层的LTU层
• 每层包含一个偏移神经元
  若一个ANN包含两个及两个以上隐藏层，则被称为深度神经网络（DNN）

使用反向自动梯度下降微分的梯度下降法训练MLP：
对每个训练实例，算法计算每个连续层的每个神经元的输出（正向过程）；然后度量网络输出误差（期望值与实际输出差值），计算最后一个隐藏层的每个神经元对输出神经元的误差贡献，持续计算至输入层。（这个反向传递有效衡量网络中所有连接权重的误差梯度）

反向传播的正向与反向传递都简单啊执行反向模式的自动微分。反向传播算法最后一步时对网络中所有连接权重执行梯度下降，使用之前度量的误差梯度。

简而言之：对每个训练实例，反向传播算法先做一次正向预测，度量误差，然后反向遍历每个层次度量每个连接误差贡献度，再微调每个连接权重来降低误差（梯度下降）

使算法正常工作需要把阶跃函数换成逻辑函数（σ(z) =1 / (1 + exp(–z)).）（逻辑函数有良好偏导），还可以与其激活函数一起使用：

• 双曲正切函数： tanh (z) = 2σ(2z) – 1：S形，可微分，输出（-1，1），有利于标准化，快速融合。

• ReLU函数：max(0,z)。连续，在z=0时不可微分，没有最大输出，有利于消除GB的一些问题，计算快，ReLU工作比S形更好。

MLP常用来分类，每个输出对应不同二进制分类。当每个分类互斥时，输出层被修改为soft-max函数。每个神经元输出对应相应分类概率。因信号单向流动（输入-输出），又被称为前馈神经网络（FNN）案例。

Training an MLP with TensorFlow’s High-Level API

用Estimator API训练：用tf.keras.datasets.mnist，这里需要下载到本地使用。

import tensorflow as tf
#数据集处理
from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data('mnist/mnist.npz')
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]

采用tf.estimator.DNNClassifier tf.estimator.inputs.numpy_input_fn

feature_cols = [tf.feature_column.numeric_column("X", shape=[28 * 28])]
dnn_clf = tf.estimator.DNNClassifier(hidden_units=[300,100], n_classes=10,
                                     feature_columns=feature_cols)

input_fn = tf.estimator.inputs.numpy_input_fn(
    x={"X": X_train}, y=y_train, num_epochs=40, batch_size=50, shuffle=True)
dnn_clf.train(input_fn=input_fn)

对测试集使用：

test_input_fn = tf.estimator.inputs.numpy_input_fn(
    x={"X": X_test}, y=y_test, shuffle=False)
eval_results = dnn_clf.evaluate(input_fn=test_input_fn)

看准确度：eval_results
看下预测过程：

y_pred_iter = dnn_clf.predict(input_fn=test_input_fn)
y_pred = list(y_pred_iter)
y_pred[0]

Training a DNN Using Plain（纯） TensorFlow

本节会用低级API构建模型，实现MBGB来训练MNIST。

Construction Phase

import tensorflow as tf

n_inputs = 28*28  # MNIST特征数量
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10

用占位符对X,y做部分定义

reset_graph()

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")#二维张量，一个维度实例，一个维度特征
y = tf.placeholder(tf.int32, shape=(None), name="y")

创建神经网络，X做输入（占位符会在执行期被替换），创建两个隐藏层和一个输出层。用neuron_layer()做创曾函数（输入，神经元数量，激活函数，层次名）：

def neuron_layer(X, n_neurons, name, activation=None):#输入，神经元数量，激活函数，层次名
    with tf.name_scope(name):#通过层名创建作用域:包含所有节点（可选）
        n_inputs = int(X.get_shape()[1])#通过查看第二维度（实例）决定输入数量
        #使用如前偏差进行随机初始化（使用指定偏差收敛更快，为所有隐藏值随机初始化权重值）
        stddev = 2 / np.sqrt(n_inputs)
        init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
        W = tf.Variable(init, name="kernel")#创建W（保存权重矩阵：包含每个输入与每个神经元连接权重）
        b = tf.Variable(tf.zeros([n_neurons]), name="bias")#b表示偏差，初始=0，每个神经元有个偏差参数
        Z = tf.matmul(X, W) + b#创建子图Z=X*W+b
        if activation is not None:#热值relu返回relu（z）=max(0,z),否则直接返回z
            return activation(Z)
        else:
            return Z

用它创建一个DNN，第一个隐藏层需要X做输入，依次串联：

#创建深度神经网络，两层隐藏，一层输出，层层以其为输入
with tf.name_scope("dnn"):#保持名字清晰
    hidden1 = neuron_layer(X, n_hidden1, name="hidden1",
                           activation=tf.nn.relu)
    hidden2 = neuron_layer(hidden1, n_hidden2, name="hidden2",
                           activation=tf.nn.relu)
    logits = neuron_layer(hidden2, n_outputs, name="outputs")#经过softmax激活之前神经网络输出（softmax随后计算）

交叉熵作为loss成本函数，sparse_softmax_cross_entropy_with_logits（比softmax更高效）根据logits计算交叉觞，期望分类以整数标记。使用TF的reduce_mean()计算平均交叉熵。

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
                                                              logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

定义梯度下降优化器使成本函数最小化：

learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

将精度做性能指标 计算模型：

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)#检查最高logit确定神经网络预测是否正确，in_top_k发明会布尔类型一维张量
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))#性能指标

创建节点初始变量，保存模型：

init = tf.global_variables_initializer()
saver = tf.train.Saver()

构建期创建了用于输入的palceholders

Execution Phase

#定义批次和批量大小

n_epochs = 40
batch_size = 50

自定义批量截取 ：

def shuffle_batch(X, y, batch_size):
    rnd_idx = np.random.permutation(len(X))#打乱
    n_batches = len(X) // batch_size
    for batch_idx in np.array_split(rnd_idx, n_batches):
        X_batch, y_batch = X[batch_idx], y[batch_idx]
        yield X_batch, y_batch

训练模型：

with tf.Session() as sess:
    init.run()#初始化所有变量
    for epoch in range(n_epochs):#周期：迭代一组批次
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):#通过上述函数迭代
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Batch accuracy:", acc_batch, "Val accuracy:", acc_val)

    save_path = saver.save(sess, "./my_model_final.ckpt")

Using the Neural Network

with tf.Session() as sess:
    saver.restore(sess, "./my_model_final.ckpt") #用硬盘存在模型 or better, use save_path
    X_new_scaled = X_test[:20]#缩放
    Z = logits.eval(feed_dict={X: X_new_scaled})
    y_pred = np.argmax(Z, axis=1)#仅预测

Using dense() instead of neuron_layer()：

n_inputs = 28*28  # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10

reset_graph()

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")

with tf.name_scope("dnn"):
    hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
                              activation=tf.nn.relu)
    hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
                              activation=tf.nn.relu)
    logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
    y_proba = tf.nn.softmax(logits)

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()
saver = tf.train.Saver()

n_epochs = 20
n_batches = 50

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_valid = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Batch accuracy:", acc_batch, "Validation accuracy:", acc_valid)

    save_path = saver.save(sess, "./my_model_final.ckpt")

Fine-Tuning Neural Network Hyperparameters

神经网络灵活既是长处，也是短板（有太多超参数需要调整），包括层数、神经元数、激活函数类型、初始化逻辑权重。可以用网格搜索（太耗时）,用随机搜索好得多，另一个方法就是用Oscar工具。

Number of Hidden Layers

从单一隐藏层开始通常效果不错，虽然单层能解决大多数问题（神经元数量够多），但多层效率更高（少神经元构造复杂函数）.

DNN擅长按照层次结构组织：低级隐藏层用建模底层结构，中级隐藏层组合地层结构，高级隐藏层和输出层组合中层结构构建高层结构。

分层架构不仅可以帮助DNN更快归纳出好方案，还可以提高对新数据集泛化能力（可用底层或中层组合新模型）

大多数问题一到两个隐藏层足以，可以逐步增减隐藏层层次，直到在训练集上过度拟合。常见的是用别人训练好的模型处理类似的网络（训练快，数据量少）

Number of Neurons per Hidden Layer

输入输出层的神经元数由任务要求的输入输出类型决定。举个例子：MNIST需要28*28个输入神经元，10个输出神经元。用漏斗形定义隐藏层尺寸，每层神经元依次减少（低级功能可合并为量更少的高级功能）。

一个典型的MNIST神经网络有两个隐藏层，第一层有300个神经元，第二层有100个。也可以定义为各150个，可以逐步增加神经元数量至过度拟合（有点玄学）。增加每层神经元数量比增加层数产生更多消耗。

一个更简单做法是采用stretch pants做法：使用更多的层数和神经元，通过提前结束训练来避免过度拟合。

Activation Functions（激活函数）

对于隐藏层：大多数情况下用ReLU激活函数（或变种）足够.
对于输出层：softmax激活函数对于分类任务，回归任务可以不使用激活函数。