16_数据结构及算法设计技术应用：下午第四题（代码题，难）

不搞清这8大算法思想，刷再多题效果也不好的
常见算法题

16.1 数据结构及算法应用前言

属于下午题中的难题
掌握：基本的填空题，拿到6~8分即可

16.2 分治法

• 思想：将一个大的，难的问题分解成若干个小问题，小问题解决完之后，再将这些小问题进行合并，得到原来初始问题的解决方案。
• 时间复杂度【O(nlgn)】

16.3 分治法(递归技术>需要掌握)

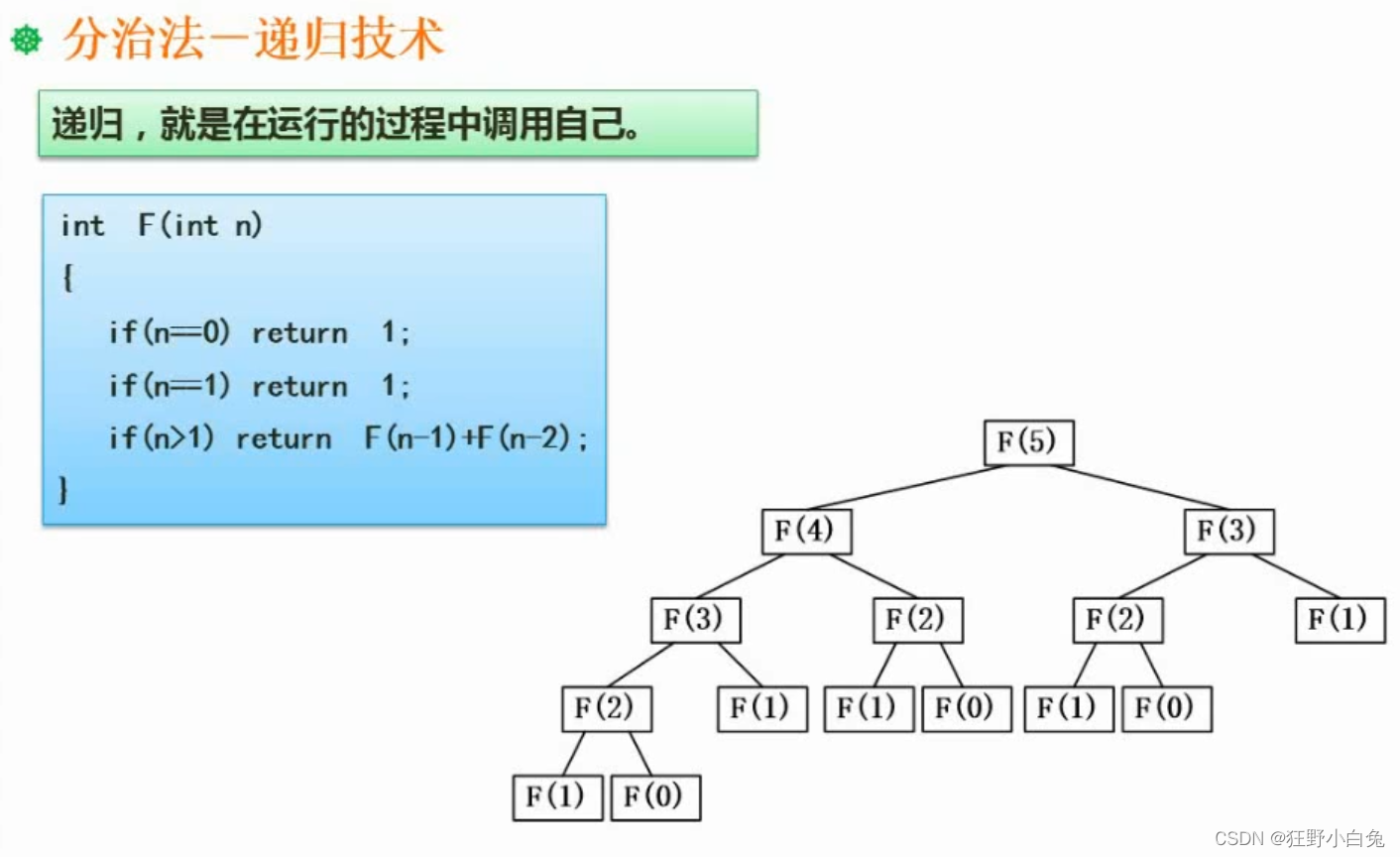
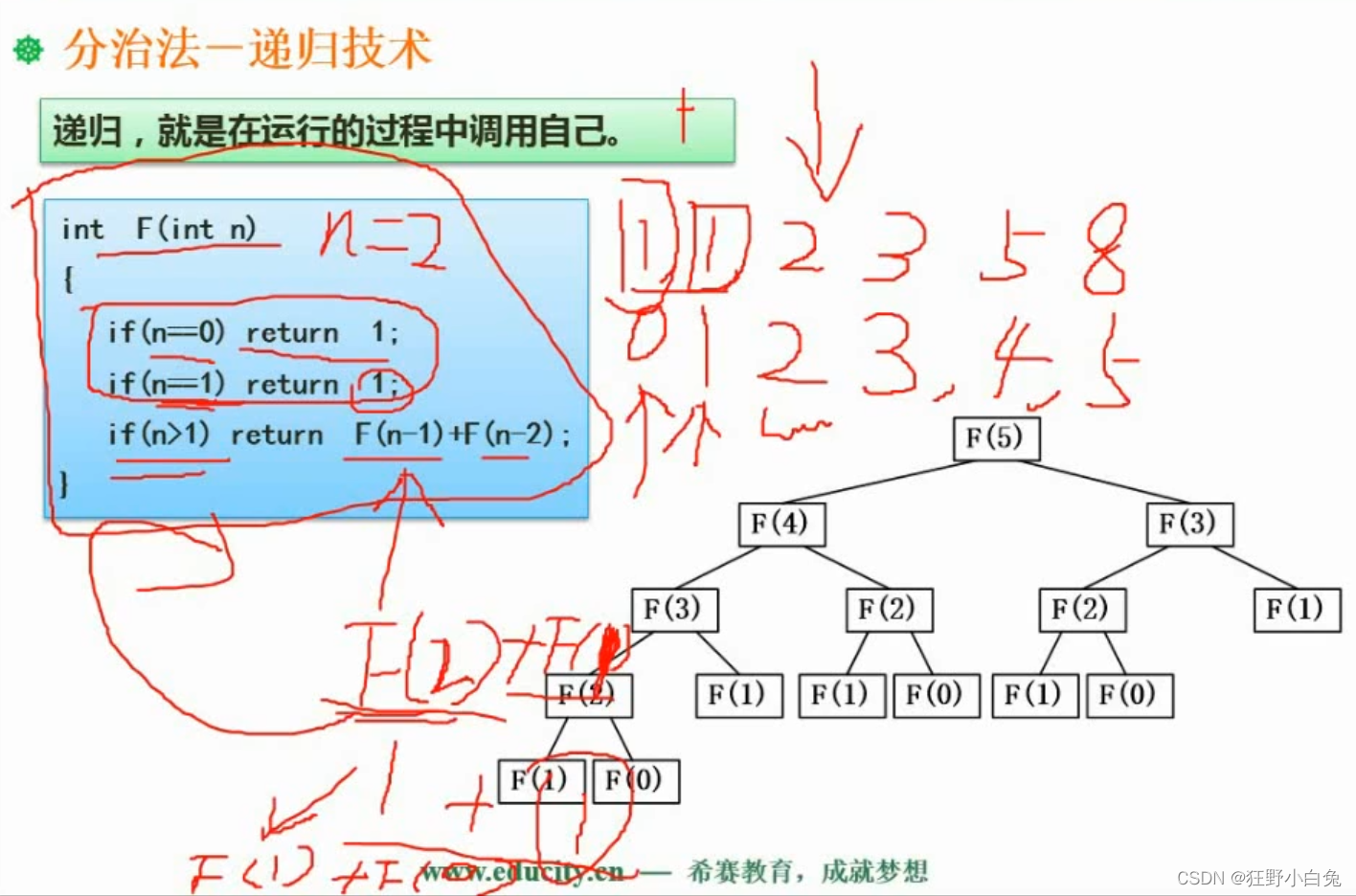
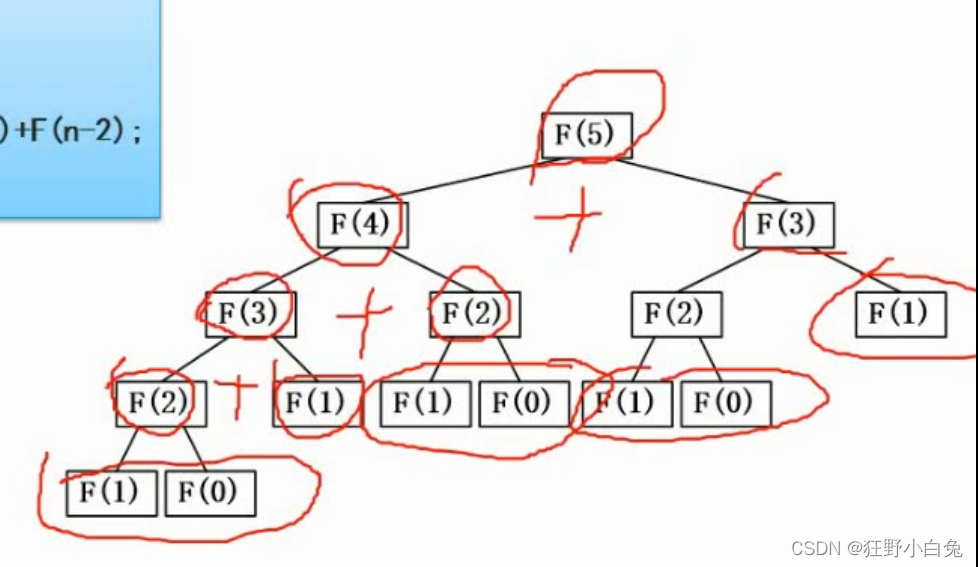
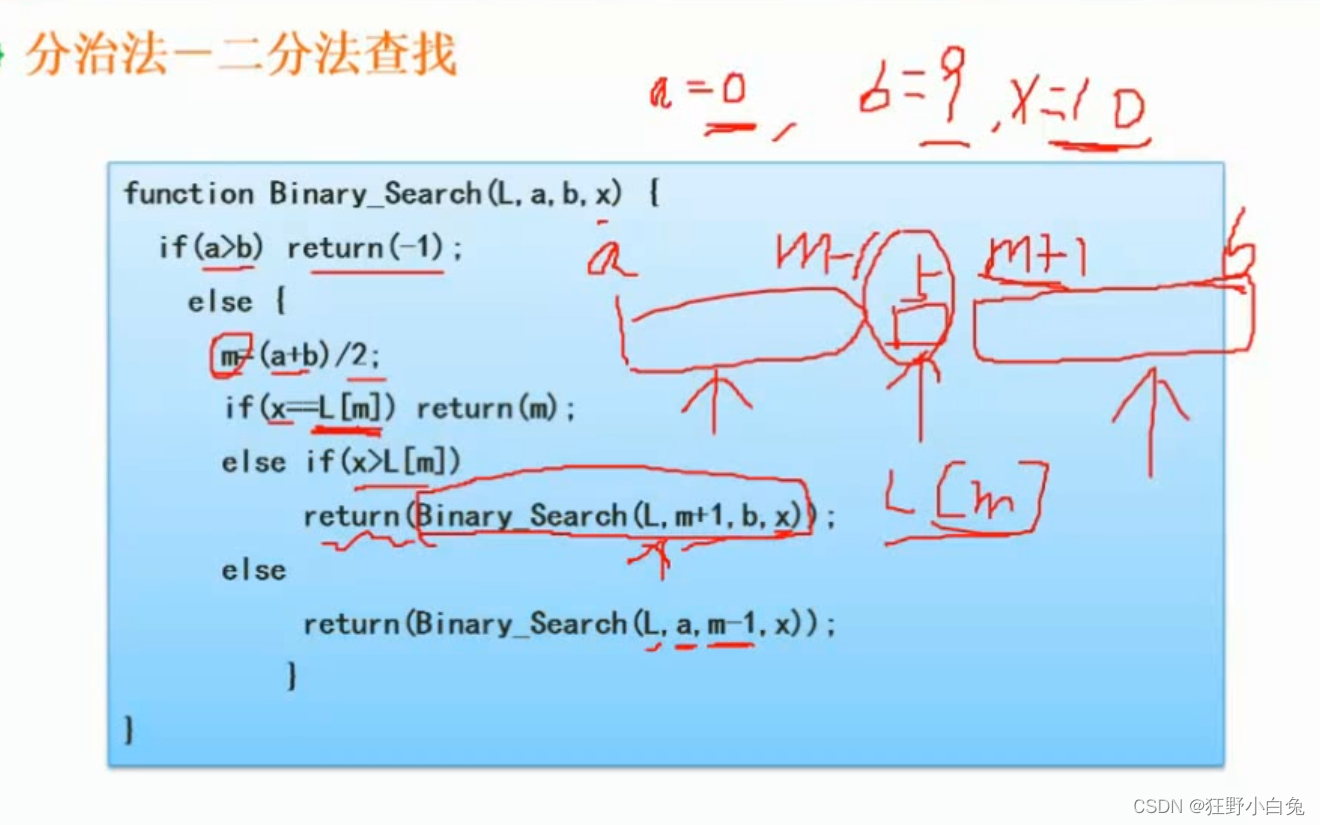
16.4 分治法(二分查找)

二分查找是分治法的具体应用
二分查找利用分治法的思想来做的

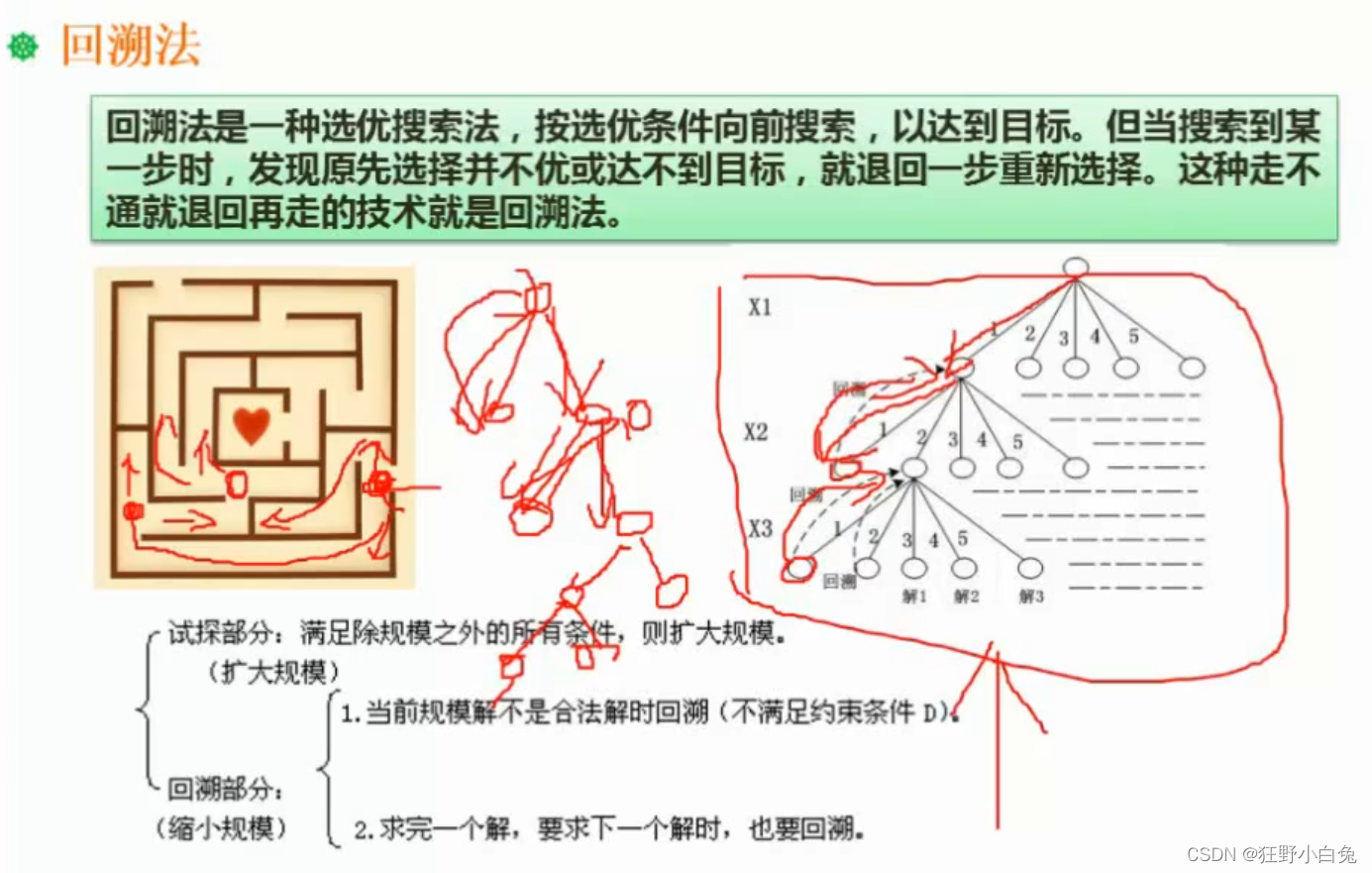
16.5 回溯法

深度优先搜索法
可以用来解决：迷宫问题

• 通过回溯法我们可以把所有的解探出来
• 也可以探出一个解（我们的目标）

• 时间复杂度：O(n!)
  • O(n!)表示当n增大时，所需的时间增长数量级的指数是n的阶乘。例如，当n从1增加到2时，时间复杂度为O(2!) = O(2*1) = O(2)，当n从2增加到3时，时间复杂度为O(3!) = O(6)，当n从3增加到4时，时间复杂度为O(4!) = O(24)。

16.6 贪心法

思想与试题判断：每一步都能选到最好的东西【每一步都取最优】，往往能得到一个不错的结果，但是很难达到最优解【画有限的时间，找到一个令人满意的解】

• 贪多，贪好
• 时间复杂度：O(n^2)

可以用来解决：背包问题

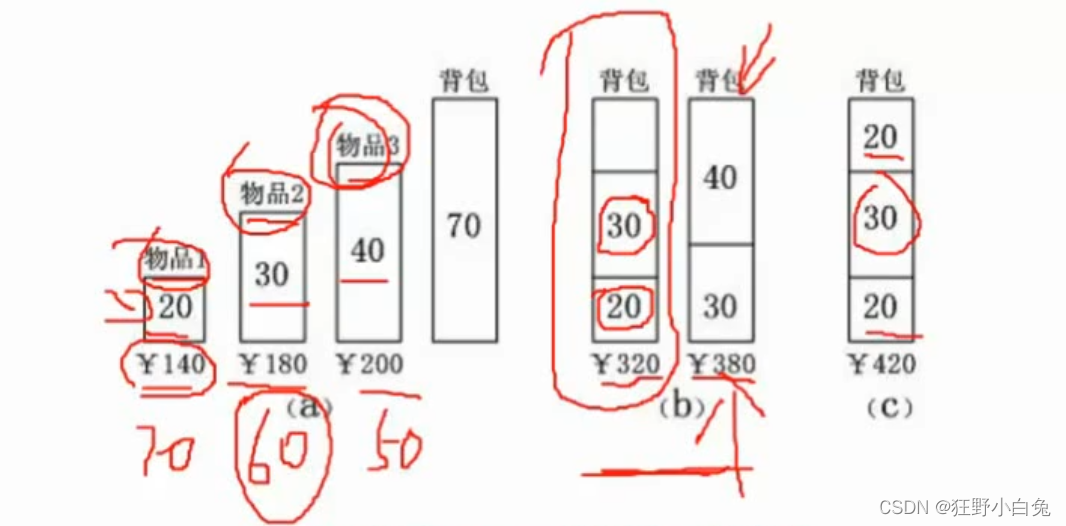
• 问：有三个物分别是不同的价格，我们只有一个容量70的背包，我们希望背包能尽可能背更多的东西，容量达到最高值，价值达到最高。
• 考虑流程：
  • 单位物品价值高的，优先拿
  • 贪心法：先拿20，再拿30，就拿不了40了，所以结果就是320元
  • 最优解：应该是30和40，结果是380元
• 注：如果可以重复最优方案是2个物1，一个物2，结果是420元

16.7 动态规划法

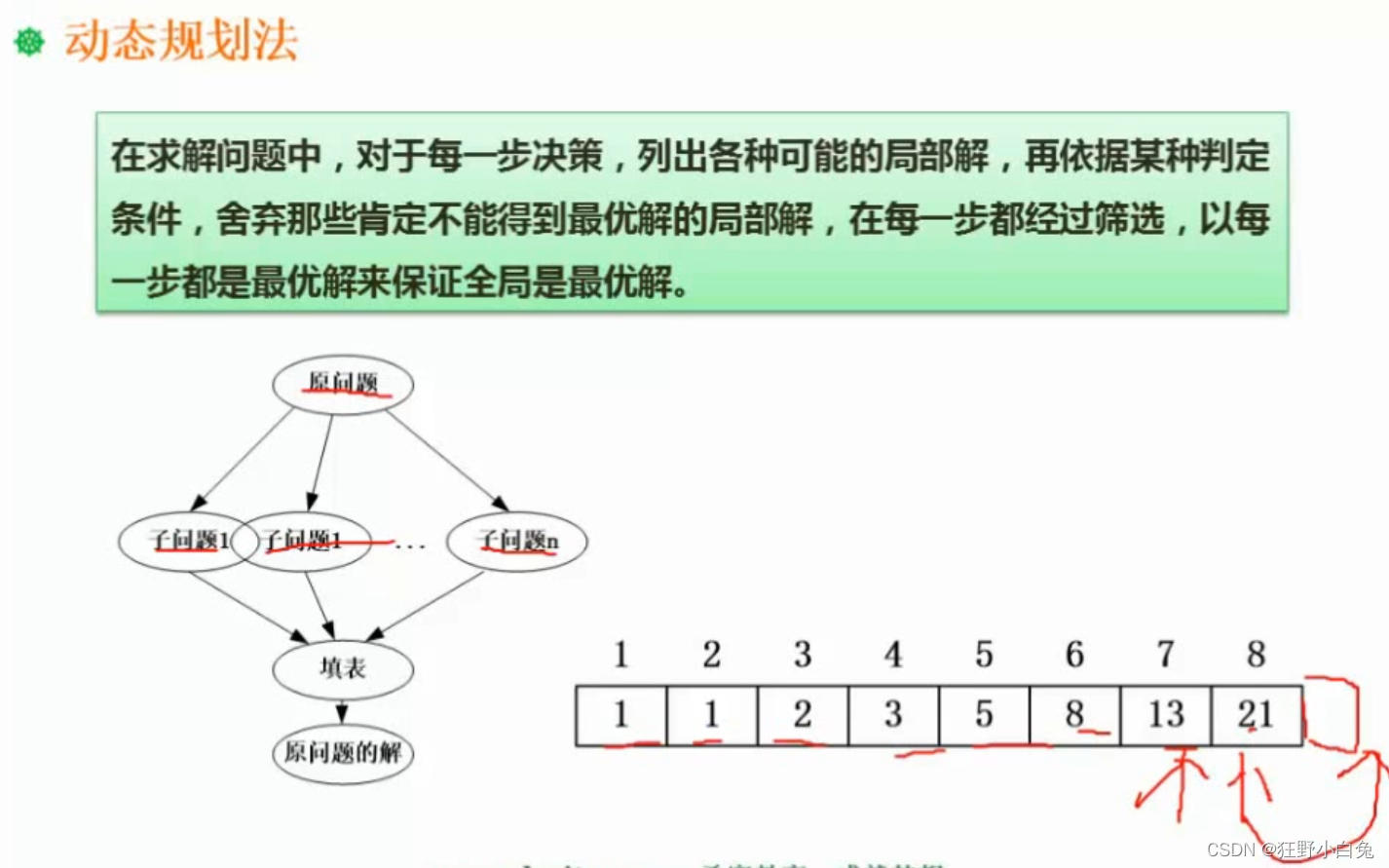
动态规划法与分治法如何区分

动态规划法：基本上都要用到查表的方式来解决问题

• 拆出的子问题不一定是独立的，我们会把子问题的解，一个一个存下来，在求更复杂解的时候，可以通过查表的方式来得到后面的问题

以斐波那契数列为例

动态规划法会将每一个值求出来存到一个数组里，当求后面一项的时候，只需要查表将表中前两项的值拿出来得到后面的值即可。

自底向上和自顶向下的时间复杂度

自底向上【常用】：O(n^k)，其中有几个for循环，k的值就是多少
自顶向下：O(2^n)

例题讲解【2017上，62】

题目

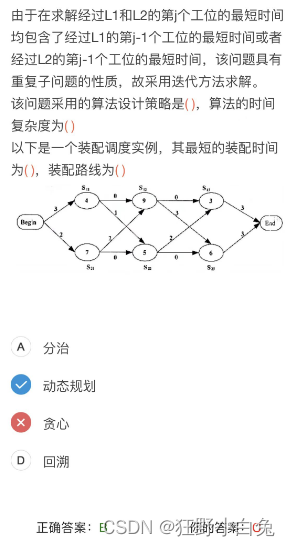
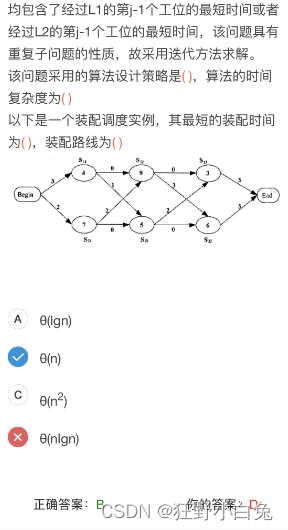
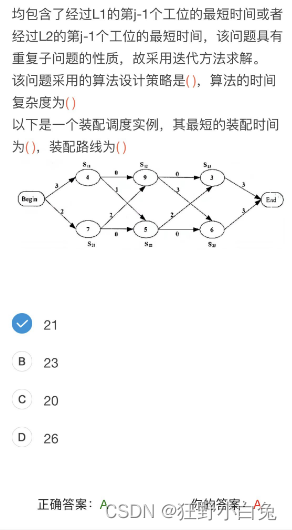
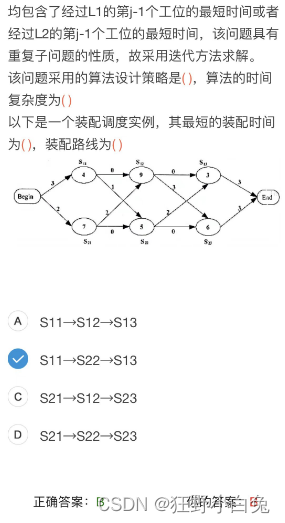
解题一

解题二

16.8总结

• 1、分治法特征：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决；否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。
• 2、动态规划法[对于得到一个最优解是动态规划的特点]：在求解问题中，对于每一步决策，列出各种可能的局部解，再依据某种判定条件，舍弃那些肯定不能得到最优解的局部解，在每一步都经过筛选，以每一步都是最优解来保证全局是最优解。本题情景没有列出所有的可能解进行筛选，因此，本题不属于动态规划法。
• 3、回溯法[可以得到问题所有的最优解，是回溯法的特征]：回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当搜索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择。这种走不通就退回再走的技术就是回溯法。本题情景没有探索和回退的过程，因此，本题不属于回溯法。
• 4、贪心法：总是做出在当前来说是最好的选择，而并不从整体上加以考虑，它所做的每步选择只是当前步骤的局部最优选择，但从整体来说不一定是最优的选择。由于它不必为了寻找最优解而穷尽所有可能解，因此其耗费时间少，一般可以快速得到满意的解，但得不到最优解。
• 5、分治界限法：类似于回溯法，也是一种在问题的解空间树T上搜索问题解的算法，但在一般情况下，分支界限法与回溯法的求解目标不同。分支界限法的求解目标是****找出满足约束条件的一个解即可。由于求解目标不同，其探索方式与回溯法也不同，分支界限法以广度优先或以最小耗费优先的方式搜索解空间树。

例题讲解【2021上】