七、(机器学习)-Tensorflow实现逻辑斯蒂回归

一、逻辑斯蒂回归

利用手写数字实现逻辑斯蒂回归，在线性感知算法中，我们使用f(x) = x函数，作为激励函数，而在逻辑斯蒂回归中，我们将采用sigmoid函数作为激励函数，所以它被称为sigmoid回归也叫做对数几率回归，需要注意的是，虽然它的名字中带有回归，但事实上它并不是一种回归算法，而是一种分类算法，它的优点是，它是直接对分类的可能性进行建模的，无需进行实现的假设数据分布，这样就避免了假设分布不准确所带来的问题，因为它是针对于分类的可能性进行建模的，所以它不仅能预测出类别，还能得到该类别的概率。
逻辑斯蒂回归是针对线性可分问题的一种易于实现而且性能优异的分类模型，是使用最为广泛的分类模型之一，假设某件事发生的概率为p，那么这件事不发生的概率事(1-p)，我们称p/(1-p)为这件事发生的几率。取这件事发生几率的对数，定义为logit§，所以logit§ 为$$Logit(p)=log\frac{p}{(1-p)}$$

因为logit函数的输入值取值范围是[0, 1]因为p为某件事发生的概率，所以通过logit函数可以将输入区间为[0, 1]转换到整个实数范围内的输出，log函数的图像如下：

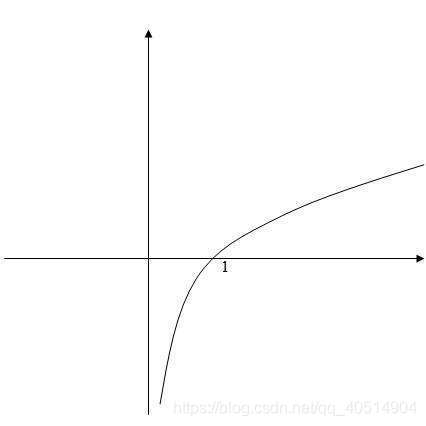
将对数几率记为输入特征值的线性表达式如下：

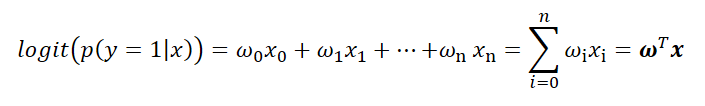
其中,p(y=1|x)为，当输入为x时，它被分为1类的概率为p，也属于1类别的条件概率。而，实际上我们需要的是给定一个样本的特征输入x，而输出是一个该样本属于某类别的概率。所以，我们取logit函数的反函数，也被称为logistic函数也就是sigmoid函数


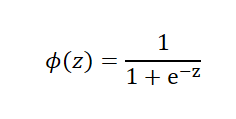
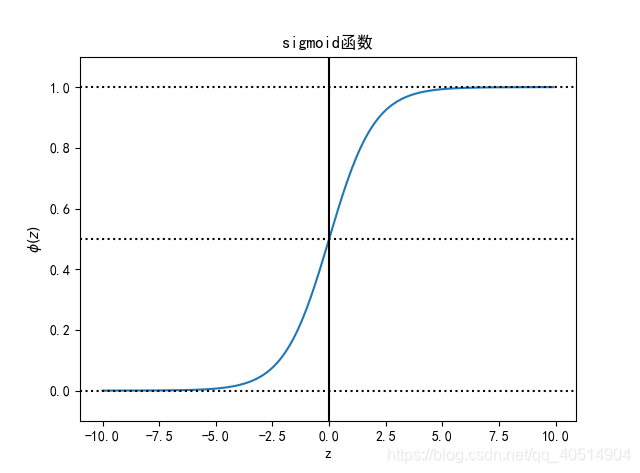
ϕ(z)中的z为样本特征与权重的线性组合。通过函数图像可以发现sigmoid函数的几个特点，当z趋于正无穷大的时候，ϕ(z)趋近于1，因为当z趋于无穷大的时候，e^(-z) 趋于零，所以分母会趋于1，当z趋于负无穷大的时候，e^(-z)会趋于正无穷大，所以ϕ(z)会趋于0。如在预测天气的时候，我们需要预测出明天属于晴天和雨天的概率，已知根天气相关的特征和权重，定义y=1为晴天，y=-1为雨天，根据天气的相关特征和权重可以获得z，然后再通过sigmoid函数可以获取到明天属于晴天的概率ϕ(z)=P(y=1|x)，如果属于晴天的概率为80%，属于雨天的概率为20%，那么当ϕ(z)>=0.8时，就属于雨天，小于0.8时就属于晴天。我们可以通过以往天气的特征所对应的天气，来求出权重和ϕ(z)的阈值，也就是天气所说的0.8。逻辑斯蒂回归除了应用于天气预测之外，还可以应用于某些疾病预测，所以逻辑斯蒂回归在医疗领域也有广泛的应用。

二、求逻辑斯蒂回归的权重

在线性感知器中，我们通过梯度下降算法来使得预测值与实际值的误差的平方和最小，来求得权重和阈值。前面我们提到过某件事情发生的几率为p/(1-p)，而在逻辑斯蒂回归中所定义的代价函数就是使得该件事情发生的几率最大，也就是某个样本属于其真实标记样本的概率越大越好。如，一个样本的特征x所对应的标记为1,通过逻辑斯蒂回归模型之后，会给出该样本的标记为1和为-1的概率分别是多少，我们当然希望模型给出该样本属于1的概率越大越好，正因为我们的代价函数需要求的是最大值，所以后面会使用到梯度上升算法而不是梯度下降算法。为了求得记录的最大值，我们需要使用最大似然函数L，假定数据集中的每个样本都是相互独立的，L(w)的计算公式如下

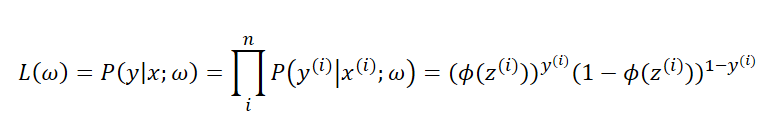
通过上面的公式可以发现，可以会出现数值溢出的情况为了降低这种情况发生的可能性和方便对似然函数进行最大化处理，取似然函数的对数

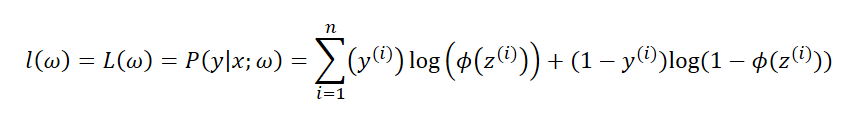
通过梯度上升算法求最大化似然函数的对数或者在将似然函数的对数乘以-1使用梯度下降算法进行最小化，通过上面的公式可以发现，当y=0的时候，第一项为0，当y=1的时候第二项为0，损失函数如下

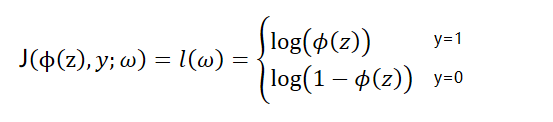
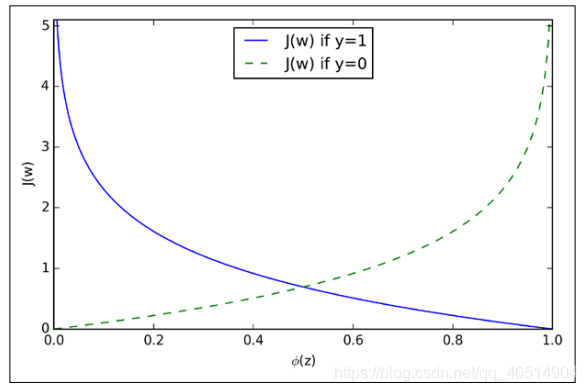
通过上图，可以观察到，当样本被正确的划分的时候损失函数是接近与0的，当样本被错误的划分的时候损失函数是趋于无穷大，这就意味着错误的预测所带来的代价将会越来越大，相对于之前的线性感知器而言，logistic回归错误预测所带来的代价要大的多。
logistic回归权重更新，相对于之前的线性感知器而言，我们只需要修改激活函数和代价函数。在实现logistic回归之前，需要先计算出对数似然函数对于w的偏导，得到每次权重更新的Δω。
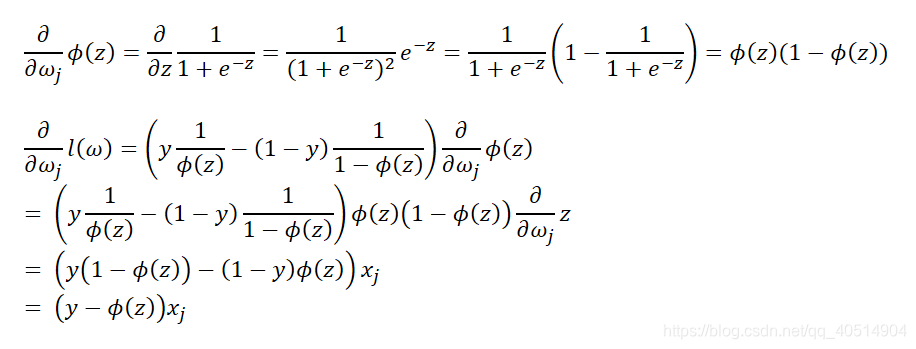所以Δω应该为

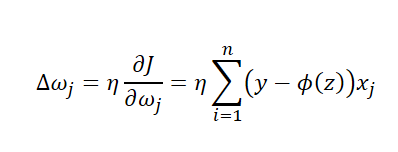
如果使用梯度下降算法，则ω=ω-Δω，如果使用梯度上升算法ω=ω+Δω。

三、代码

import warnings
warnings.filter('ignore')

import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist 是美国一个研究机构的缩写
Tensorflow中很多的案例都是使用这个样本集
60000张训练数据，10000张测试数据

mnist = input_data.read_data_sets('./')
mnist

mnist.validation.images.shape
mnist.train.image.shape
mnist.test.image.shape
mnist.train.labels[:50]

加载数据，目标值变成概率的形式

mnist = input_data.read_data_sets('./', one_hot=True)
mnist.train.images.shape
mnist.test.images.shape
mnist.train.labels[:10]

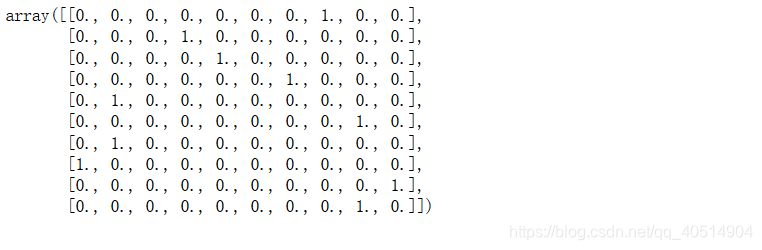
构建方程

X = tf.placeholder(dtype=tf.float64, shape=(None, 784), name='data')
y = tf.placeholder(dtype=tf.float64, shape=(None, 10), name='target')
W = tf.Variable(initial_value = tf.zeros(shape=(784, 10), dtype=tf.float64))
b = tf.Variavle(initial_value = tf.zeros(shape=(10), dtype=tf.float64))

y_pred = tf.matmul(X,W) + b

构建损失函数
y 和 y_进行对比
y表示是概率 [0， 0， 0， 0， 0， 0， 1， 0， 0， 0]
y_pred矩阵运算求解的目标值
要将y_pred转化为概率，利用softmax
此时y和y_表示概率
y和y_越接近，说明预测函数越准确

y_ = tf.nn.softmax(y_pred)

此时是回归问题，不能使用最小二乘法
这里我们使用交叉熵来表示损失函数
熵:$$entropy=-\sum _{i=0}^{N}pi\ast lo{g}_{2}pi$$

交叉熵:qi为预测的概率，pi为真实的概率$$cross-entropy=\sum _{i=0}^{N}pi\ast lo{g}_2\frac{1}{qi}$$
损失函数越小越好
平均交叉熵 ----> 可比较大小的数

loss = tf.reduce_mean(tf.reduce_sum(tf.multiply(y, tf.log(1/y_)), axis=-1))

最优化

opt = tf.train.GradientDescentOptimizer(0.01).minmize(loss)

训练

epoches = 100
saver = tf.train.Saver()

with tf.Session() as sess:
	sess.run(tf.global_variables_initializer())
	
	for i in range(epoches):
		c = 0
		for j in range(100):
			X_train, t_train = mnist.train.next_batch(550)
			opt_, cost = sess.run([opt, loss], feed_dict = {X:X_train , y:y_train})
			c += cost/100
		# 计算准确率
		X_test, y_test = mnist.test.next_batch(2000)
		y_predict = sess.run(y_, feed_dict = {X:X_test})
		y_test = np.argmax(y_test, axis=-1)
		y_predict = np.argmax(y_predict, axis=-1)
		accuracy = (y_test == y_predict).mean()
		print('执行次数:%d, 损失函数是:%0.4f,准确率是：%0.4f'%(i+1, c, accuracy))
		if accuracy > 0.91:
			saver.save(sess, './model/estimator', global_step = i)
			print('-------------模型保存成功------------')

保存了上次的训练模型，在上一次训练的基础上继续进行学习

with tf.Session() as sess:
	# 还原到sess会话中
	saver.restore(sess, './model/estimator-99')
	for i in range(100, 200):
		c = 0
		for j  in range(100):
			X_train,y_train = mnist.train.next_batch(550)
			opt_, cost = sess.run([opt,loss], feed_dict = {X:X_train, y:y_train})
			c += cost/100
		# 计算准确率
		X_test, y_test = mnist.test.next_batch(2000)
		y_predict = sess.run(y_, feed_dict={X:X_test})
		y_test = np.argmax(y_test, axis=-1)
		y_predict = np.argmax(y_predict, axis=1)
		accuracy = (y_test == y_predict).mean()
		print('执行次数:%d,损失函数是:%0.4f,准确率是:%0.4f'%(i+1, c , accuracy))
		if accuracy > 0.91:
			saver.save(sess, './model/estimator', global_step=i)
			print('模型保存成功!')

---

望您：
“情深不寿，强极则辱，谦谦君子，温润如玉”。