dymola学习笔记第二天——求解非线性方程

最新推荐文章于 2024-05-12 21:01:19 发布

东北亚见熊

最新推荐文章于 2024-05-12 21:01:19 发布

阅读量2.1k

点赞数 2

CC 4.0 BY-SA版权

分类专栏： dymola

本文链接：https://blog.youkuaiyun.com/qq_40196524/article/details/97644940

这篇博客介绍了如何在Dymola中使用Modelica文本定义和模拟平面数学摆的非线性方程。作者详细阐述了设置参数、变量的过程，并展示了如何处理未完全指定的初始条件警告。最后，提到了通过增加单位计算来改进模拟的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

此示例将说明如何定义由常微分方程给出的简单模型。我们将模拟平面数学摆，如图所示。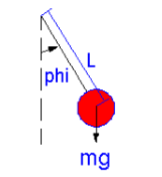在这里插入图片描述
m是质量，L是从支撑到质心的距离。让我们假设弦是不可扩展的和无质量的，而且，让我们忽略空气的阻力并假设引力场与g作为重力加速度是恒定的。摆锤的运动方程由原点周围的扭矩平衡给出

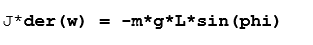
其中J是相对于原点的惯性矩。假设点质量给出
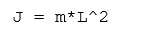
在这里插入图片描述
变量w是角速度，der（w）表示w的时间导数，即角加速度。对于我们的角度位置der(phi) = w
启动Dymola或如果它已经启动，则在Dymola主窗口中输入命令File> Clear All。单击右下角的“建模”选项卡。然后选择File> New> Model …
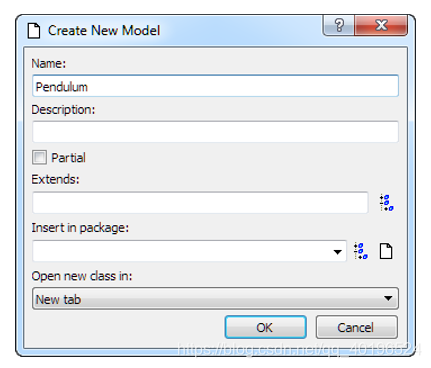
在这里插入图片描述
此模型将添加到顶层。您通常应将模型存储到包中，如稍后所述。将使用新模型打开一个新选项卡。选项卡的工作方式类似于Internet Explorer中的工作区域。可以在不同视图中检查和编辑模型。当直接根据方程式指定行为时，最方便的是将模型用作Modelica文本; 也就是说，在编辑窗口的Modelica文本层中工作。要显示此图层，请按Modelica文本工具栏按钮（第二个最右侧的工具按钮）