文字错误部分标红的实现（使用最小编辑距离算法）

文字错误部分标红的实现（使用最小编辑距离算法）

首先要实现标红最好先理解最小编辑距离算法，网上有很多教程，都比较简单，下面我也会再讲一遍，这里先给一个我参考的

https://blog.youkuaiyun.com/qq_34552886/article/details/72556242

如果已经了解最小编辑距离算法，直接看"标红实现"部分

实现文字标红的关键也就是找到两段字符串中不同的部分，而最小编辑距离算法的作用就是找到把字符串A转换成字符串B所需要的最少操作数，我们把这种操作分三类：

• 删除 delete
• 插入 insert
• 替换 replace

最小编辑距离算法

最小编辑距离算法的个人理解：

最小编辑距离的核心思想其实是类似数学归纳法，通过建立一个二维矩阵的方法来得到从字符串a到b的最小编辑次数；

核心逻辑：

• 1、字符串A、B（长度分别为a、b），若A的最后一个字符和B的最后一个字符一致，则A→B的最小编辑距离也就等于(A-1)→(B-1)的最小编辑距离（A-1，表示A的前a-1个字符组成的子字符串）；若A的最后一个字符和B不同，则A→B的最小编辑距离也就等于(A-1)→(B-1)、(A-1)→B、A→(B-1)三者的最小编辑距离中的最小值加一。
• 2、当A的长度为0时，A→B的最小编辑距离也就是B的长度

举例分析：

依据上面的逻辑，我们就可以开始逐步建立二维矩阵了，或者说叫做动态规划方程

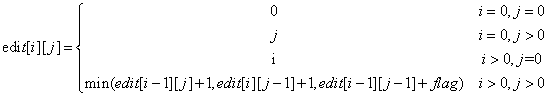
edit[i][j]表示A串和B串的编辑距离。edit[i][j]表示A串从第0个字符开始到第i个字符和B串从第0个字符开始到第j个字符，这两个字串的编辑距离。

举例来讲，比如字符串A“最小编辑距离算法”和B“最短路径算法”

	A	最	小	编	辑	距	离	算	法
B	0	1	2	3	4	5	6	7	8
最	1
短	2
路	3
径	4
算	5
法	6

如上图：矩阵每个数值代表改行对应的A的子字符串到B的子字符串的最小编辑距离（或者从B到A）

根据核心逻辑2，我们可以填充第一行和第一列

然后依据核心逻辑，可以逐行进行矩阵填充。

	A	最	小	编	辑	距	离	算	法
B	0	1	2	3	4	5	6	7	8
最	1	0	1	2	3	4	5	6	7
短	2	1	1	2	3	4	5	6	7
路	3	2	2	2	3	4	5	6	7
径	4	3	3	3	3	4	5	6	7
算	5	4	4	4	4	4	5	5	6
法	6	5	5	5	5	5	5	6	5

填充完成后，矩阵右下角的数值也就是从字符串A、B之间的编辑距离。

标红实现：

上述内容就是最小编辑距离算法，下面我们分析怎样通过上述算法实现标红：

分析：

要标红，也就是要找到两个字符串中不同的部分，而结合编辑距离的概念，把字符串A变成B需要一系列，插入、删除、替换的操作，如果要对A进行标红，那么我们就需要找到，需要被删除、替换的部分（插入操作，因为A中不存在这一部分字符串，所以无法标红）。

也就是说我们要找到从A到B的达到最短编辑距离所需要经过的路径，具体就是从A到B需要在什么位置，进行什么操作。

逆推得到路径：

直接逆推矩阵就能得到经过的路径，核心逻辑如下：

• 若当前位置，对应A、B子字符串尾字符相同，则逆推到左上角元素，其实际含义就是当前位置文字相同，不需要编辑，所以不标红
• 若当前位置，对应A、B子字符串尾字符不同，则找到左、左上、上三个元素中最小值
  • 若左最小，逆推到左边元素，其实际含义是，需要行字符串（本例中的B）插入一个字符，或者列字符串（A）删除一个字符
  • 若上最小，逆推到上边元素，其实际含义是，需要行字符串删除一个字符，或者列字符串插入一个字符
  • 若左上最小，逆推到左上角元素，其实际含义是，需要行字符串将最后一个字符替换为和列字符串相同的字符（或者行列互换）

重复上述过程知道逆推到矩阵左上角即可，实际算法中可以逆推到你要标红的字符串对应行或者列值为0即可。

举例：

我们要对字符串A标红，则逆推到 j=0（j表示当前列数）即可，当j = 0以后，无论i为多少，都只剩下向上这一个方向，也就是A需要插入i个元素，A中这些元素不存在，所以此时可以直接跳出循环

	A	最	小	编	辑	距	离	算	法
B	0	1	2	3	4	5	6	7	8
最	1	↖=0	1	2	3	4	5	6	7
短	2	1	↖≠1	2	3	4	5	6	7
路	3	2	2	↖≠2	3	4	5	6	7
径	4	3	3	3	↖≠3	←≠4	←≠5	6	7
算	5	4	4	4	4	4	5	↖=5	6
法	6	5	5	5	5	5	5	6	↖=5

箭头表示逆推的方向，=表示当前位置字符相同，≠表示当前位置字符不同

根据逆推路径，找到A需要进行的删除、替换操作，也就是**”←≠”和“↖≠”**

所以最终结果：

“最小编辑距离算法” → “最短路径算法”

下划线表示需要替换、加粗表示需要删除，要实现标红的话就都标红就好。