链表-链表中环的入口结点

题目描述

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null;

题目分析

链表中某些结点构成了一个环，找打环的入口结点

思路：

  head->a1->a2->a3...

使用双层循环，例如对于结点a1，遍历整个链表判断是否有a1 = head->next；(head = head->next);a2,a3,......an;依次

测试报错，没通过

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};*/

class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        //找到某个结点地址与链表中默认结点的next指针域的地址相同，即为链表中的环
        //定义一个
        ListNode* temp = pHead;
        //定义一个遍历结点p
        ListNode* p = temp；
         //循环条件：遍历结点非空;需要使用双层循环，类似“冒泡”找出链表中的环
        while(temp){
             while(p){
                 p = p->next;
                 if（temp != p）{
                     p = p->next;
                }
                 else{
                     return temp;
                     break;
                 }
             }
            temp = temp->next;
        }
        if(temp == NULL){
            return null;
        }
        }
};

另外，参考：却顾所来径

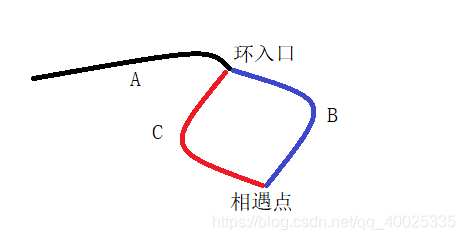
step1、找两者相遇点

设置两个指针，快指针fast每次走两个结点的距离，慢指针slow每次走一个结点的距离；

链表中没有环，直到走完整个链表，slow不可能追上fast；

链表中有环，fast先进环，绕环走，slow后进环，相相当于fast在追slow，两者一定会相遇；

step2:

两个指针，slow从表头开始走，fast从相遇点开始走（两者速度一样，每次走一个结点），最后一定相遇与环入口；

表头到环入口的距离为A；环入口到相遇点的距离为B；相遇点到环入口距离为C；

实现过程：

1、当fast、slow两者相遇时，快指针的路程是慢指针路程的两倍：

（因为两者走是同步的，只不过fast速度是slow的两倍，不管相不相遇，同一时刻，fast走的路程都是slow的两倍）

fast走的路程：A+（B+C）*K+B

slow走的路程：A+B

（A+B）*2 = A+（B+C）*K+B  --》 A = （K-1）*（B+C）+C         （1） 

 即，链表头到环入口的距离 = 相遇点到环入口距离 + 环长度*（K-1）

2、记录相遇结点之后，让fast从相遇结点开始走，slow从表头开始走，两者一定在环入口相遇。

为什么会在环入口相遇？根据公式（1）计算得到

class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        //先找fast与slow相遇点
        ListNode* fast = pHead;
        ListNode* slow = pHead;
        if（pHead == nullptr || pHead->next == nullptr）
        {
            return nullptr;
        }
        while(fast && slow){
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow){
                break;
            }else{
                return nullptr；
            }
                
        }
        //fast从相遇点出发，slow从表头出发
        slow = pHead;
        while(fast != slow){
            fast = fast->next;
            slow = slow->next;
        }
        return fast;
    }
};

测试通过代码

class Solution{
public:
	ListNode *EntryNodeOfLoop(ListNode* pHead){
		ListNode* fast = pHead;//fast从表头出发 
		ListNode* slow = pHead;//slow从表头出发 
		while(fast && fast->next){  // 表头及表头下一个结点不为null 
			//fast每次走两个结点的距离 
			fast = fast->next->next;
			//slow每次走一个结点的距离 
			slow = slow->next;
			//当fast == slow说明两个指针在环中相遇 
			if(fast == slow){
				break;
			}
		} 
		//此时fast 及fast->next为空，返回null 
		if(!fast || !fast->next)
			return NULL;
//		难点：slow从表头出发，fast从相遇点出发，为什么当fast和slow相遇一定是在环入口
//		本身数据结构不难，难的是，将问题抽象为数学模型		
		slow = pHead;//low从链表头出发
		while(fast != slow){
			//fast 从相遇点出发
			fast = fast->next;
			slow = slow->next; 
		} 
		return slow;
	}
};