第一周总结----2017.9.10-优快云博客

前言
正文
完求dalao多多补充有事请留言

前言:

紧张的学习又开始了.
想想上周学了什么.

正文

堆(优先队列)

又是一种奇怪的东西但是省时省力,简单粗暴.

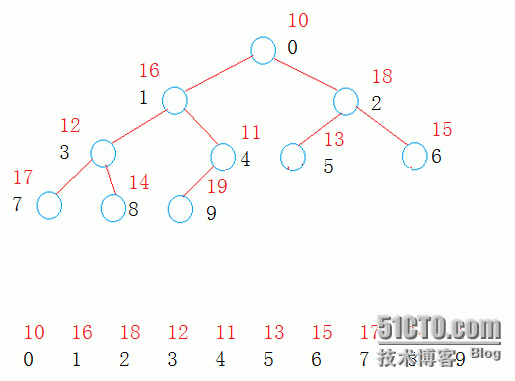
堆数据结构是一种数组对象，它可以被视为一棵完全二叉树结构。
堆结构的二叉树存储是：
最大堆：每个父节点的都大于孩子节点。
最小堆：每个父节点的都小于孩子节点。
两个最重要的是PUSH和POP。 PUSH操作在堆栈的顶部加入一个元素。POP操作相反，在堆栈顶部移去一个元素，并将堆栈的大小减一。

于是优先队列就由此生发出来了.
由于,堆的高度是log_n的,所以不论插入还是输出都是log_n的复杂度.

#include <bits/stdc++.h>
using namespace std;

const int N = 300000;

struct Heap {
    int heap[N + 10];
    int size;

    void init() {
        size = 1;
    }

    void push (int x) {
        int i = size++;
        while (i > 1) {
            int p = (i >> 1);
            if (heap[p] > x) {
                break;
            }
            heap[i] = heap[p];
            i = p;
        }
        heap[i] = x;
    }

    int pop() {
        int ret = heap[1];
        int x = heap[--size];

        int i = 1;
        while ((i << 1) < size) {
            int lson = (i << 1);
            int rson = (i << 1 | 1);
            if (rson < size && heap[rson] > heap[lson]) lson = rson;

            if (heap[lson] < x) {
                break;
            }

            heap[i] = heap[lson];
            i = lson;
        }
        heap[i] = x;
        return ret;
    }

    bool empty() {
        return size == 0;
    }
};

int a[N];

int main () {

    srand(time(NULL));


    Heap my_heap;
    my_heap.init();
    for (int i = 0; i < N; i++) {
        a[i] = rand()*rand();
    }

//start here
    clock_t mystart = clock();
    for (int i = 0; i < N; i++) {
        my_heap.push(a[i]);
    }

    while(!my_heap.empty()) {
        my_heap.pop();
    }

    clock_t myend = clock();
//end here

    priority_queue<int> heap;

    clock_t start = clock();
    for (int i = 0; i < N; i++) {
        heap.push(a[i]);
    }

    while(!heap.empty()) {
       // cout << heap.top() << endl;
        heap.pop();
    }

    clock_t end = clock();
    cout << "Running time of xjoi machine is:" << static_cast<double> (myend-mystart)/CLOCKS_PER_SEC*1000 << "ms" << endl;
    cout << "Running time stl is:" << static_cast<double> (end-start)/CLOCKS_PER_SEC*1000 << "ms" << endl;

    return 0;
}

以上程序不是我打的……
此程序是大头堆的模板,可以测试手写堆的速度.

当然可以用c++自带的堆明显手写的更快.

这里写图片描述

利用优先队列可以自动调整自身的元素,可以完成很多易超时的题目.

邻接表

奇怪的东西*2.

对于图来说，邻接矩阵是不错的一种图存储结构，但是我们也发现，对于边数相对顶点较少的图，这种结构是存在对存储空间的极大浪费的。因此我们考虑另外一种存储结构方式：邻接表（Adjacency List），即数组与链表相结合的存储方法。

邻接表是图的一种最主要存储结构,用来描述图上的每一个点。对图的每个顶点建立一个容器（n个顶点建立n个容器），第i个容器中的结点包含顶点Vi的所有邻接顶点。实际上我们常用的邻接矩阵就是一种未离散化每个点的边集的邻接表。
在有向图中，描述每个点向别的节点连的边（点a->点b这种情况）。
在无向图中，描述每个点所有的边(点a-点b这种情况)

#include<bits/stdc++.h>
using namespace std;
#define N 1000000
int first[N],next[N],point[N];
int E;
void f(int a,int b)
{
    point[E]=b;
    next[E]=first[a];
    first[a]=E;
    E++;
}
int main()
{
    memset(first,-1,sizeof(first));
    int a,c,d;
    cin>>a;
    E=0;
    for(int i=1; i<=a; i++)
    {
        cin>>c>>d;
        f(c,d);
        f(d,c);
    }
    for(int i=1; i<=a; i++)
    {
        cout<<i<<":";
        for(int j=first[i]; j!=-1; j=next[j])
            cout<<point[j];
        cout<<endl;
    }
    return 0;
}