力扣85 最大矩形的简单算法求解

最新推荐文章于 2024-03-24 15:21:08 发布

原创最新推荐文章于 2024-03-24 15:21:08 发布 · 771 阅读

1 ·

CC 4.0 BY-SA版权

算法与刷题专栏收录该内容

33 篇文章

订阅专栏

本文介绍了如何利用算法解决力扣85题，通过转化问题，将寻找最大矩形面积转化为计算每一层矩形的最大面积。文中详细分析了算法思路，并提供了代码实现，包括求以i行为底的数组tail[]的计算方法和完整代码，执行效率表现良好。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

1. 题目
2. 算法分析
3. 代码
- 3.1 求以i行为底的组成的数组tail[]
- 3.2 完整代码
4. 执行效率打败80%发现还可以

1. 题目

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

2. 算法分析

回顾力扣84题，我们可以算一个数组的最大矩形面积，题解：传送门
这道题和力扣84题是可以转化的，如图：
HCG
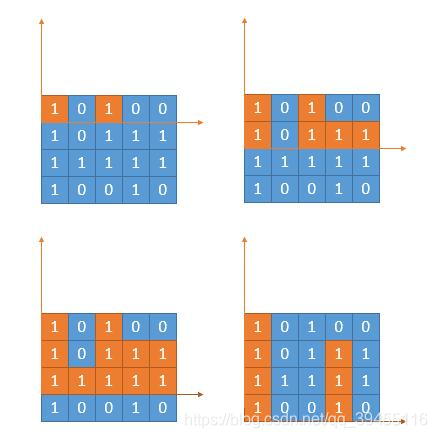
题目就转化成了计算每一层矩形的最大面积，就是求出每一层的 heights[] 然后传给利用力扣85的算法的函数就可以了。

3. 代码

3.1 求以i行为底的组成的数组tail[]

1. max 是我们最后的结果
2. 因为我们计算当前行组成的数组的值，要加上上一行组成数组的值，所以要定义两个数组
而且遍历完当前行之后，要把head[]=tail[] ，同事tail[]数组重置为0
传入求最大矩形面积的数组是当前数组taiL[]
3. head[] 是上一行为底组成的数组
4. tail[]是当前行为底组成的数组

public static int maximalRectangle(char[][] matrix) {
   if (matrix.length == 0 || matrix[0].length == 0) {
       return 0;
   }
   int max = 0;
   int col = matrix[0].length;
   int head[] = new int[col];
   int tail[] = new int[col];
   for (int i = 0; i < matrix.length; i++) {
       for (int j = 0; j < col; j++) {

           if ('1' == matrix[i][j]) {
               tail[j] = 1 + head[j];
           }
       }
       max = Math.max(largestRectangleArea(tail), max);
       head = tail;
       tail = new int[col];

   }
   return max;
}

3.2 完整代码

package com.hcg.dou;

public class Juxing {

    public static int largestRectangleArea(int[] heights) {

        int shangCiMax = 0;
        int oneMaxLen = 0;
        int oneLianNum = 1;
        if (heights.length == 0) {
            return 0;
        }
        if (heights.length == 1) {
            return heights[0];
        }
        shangCiMax = heights[0];
        int left = 0;
        int right = 0;
        for (int i = 0; i < heights.length; i++) {
            left = i - 1;
            right = i + 1;
            if (heights[i] >= shangCiMax) {
                shangCiMax = heights[i];
            }
            while (left >= 0 && heights[i] <= heights[left]) {
                left--;
            }
            left++;

            while (right < heights.length && heights[i] <= heights[right]) {
                right++;
            }
            right--;
            oneLianNum = right - left + 1;
            oneMaxLen = oneLianNum * heights[i];
            if (oneMaxLen >= shangCiMax) {
                shangCiMax = oneMaxLen;
            }

        }
        return shangCiMax;
    }

    public static int maximalRectangle(char[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int max = 0;
        int col = matrix[0].length;
        int head[] = new int[col];
        int tail[] = new int[col];
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < col; j++) {

                if ('1' == matrix[i][j]) {
                    tail[j] = 1 + head[j];
                }
            }
            max = Math.max(largestRectangleArea(tail), max);
            head = tail;
            tail = new int[col];

        }
        return max;
    }

    public static void main(String[] args) {
        char arr[][] = new char[][]{
                {'1', '0', '1', '0', '0'},
                {'1', '0', '1', '1', '1'},
                {'1', '1', '1', '1', '1'},
                {'1', '0', '0', '1', '0'},

        };
        System.out.println(maximalRectangle(arr));
    }
}

4. 执行效率打败80%发现还可以

执行用时 :14 ms, 在所有 Java 提交中击败了80.57%的用户
内存消耗 :43.1 MB, 在所有 Java 提交中击败了87.50%的用户