【剑指Offer】个人学习笔记_53 - I_在排序数组中查找数字 I&53 - II_0～n-1中缺失的数字

最新推荐文章于 2024-04-21 02:21:20 发布

原创最新推荐文章于 2024-04-21 02:21:20 发布 · 633 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二分法 #java #leetcode #算法 #数据结构

Coding 专栏收录该内容

64 篇文章

订阅专栏

这篇博客详细记录了在排序数组中查找数字和寻找缺失数字的问题，通过二分查找算法进行优化。作者分享了多种解题思路，包括基础的遍历、改进的二分查找以及双指针法，并对比了不同方法的执行效率。博客内容涵盖《剑指Offer》中的两个经典题目，旨在帮助读者深入理解排序数组的搜索技巧。

【剑指Offer】个人学习笔记 53 - I. 在排序数组中查找数字 I

刷题日期：上午9:05 2021年5月16日星期日

个人刷题记录，代码收集，来源皆为leetcode

经过多方讨论和请教，现在打算往Java方向发力

主要答题语言为Java

题目：

剑指 Offer 53 - I. 在排序数组中查找数字 I

难度简单128

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

限制：

0 <= 数组长度 <= 50000

题目分析

干就完事了，简单的方法肯定直接都能想到，就看有没有什么更优解了。

数组特点是排序好的，所以目标后面的就可以直接跳过了。

初始解答：

全部遍历的解法：

class Solution {
    public int search(int[] nums, int target) {
        int res = 0; //初始化结果
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] == target) res++;
        }
        return res;
    }
}

不考虑更大部分的

class Solution {
    public int search(int[] nums, int target) {
        int res = 0; //初始化结果
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] > target) break;
            if(nums[i] == target) res++;
        }
        return res;
    }
}

执行结果：通过

显示详情添加备注

执行用时：1 ms, 在所有 Java 提交中击败了28.20%的用户

内存消耗：40.9 MB, 在所有 Java 提交中击败了98.87%的用户

好像区别也不大，那么如果考虑二分查找呢

class Solution {
    public int search(int[] nums, int target) {
        int res = 0,l = 0, r = nums.length - 1; //初始化结果
		if(target < nums[l] || target > nums[r] || l > r){
			return res;				
		}
		while(l <= r){
			int m = (l + r) / 2;
			if(nums[m] > target){
				//比关键字大则关键字在左区域
				r = m - 1;
			}else if(nums[m] < target){
				//比关键字小则关键字在右区域
				l= m + 1;
			}else{
				res ++;
			}
        }
        return res;
    }
}

太菜了没实现，老是超出时间限制，参考方法一，好像是第一个while里面的条件和左右边缘没设置好。

class Solution {
    public int search(int[] nums, int target) {
        int res = 0,l = 0, r = nums.length - 1; //初始化结果
		while(l < r){
			int m = (l + r) / 2;
			if(nums[m] >= target){
				//比关键字大则关键字在左区域
				r = m;
			}else if(nums[m] < target){
				//比关键字小则关键字在右区域
				l= m + 1;
			}
        }
        while(l < nums.length && nums[l++] == target) {
            res++;
        }
        return res;
    }
}

执行结果：通过

显示详情添加备注

执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户

内存消耗：41.2 MB, 在所有 Java 提交中击败了87.22%的用户

K神的改进方法也很巧妙，直接找8和7的边界相减，值得推敲。

学习他人：

方法一:

ZML400

2020-03-27

执行用时 : 0 ms , 在所有 Java 提交中击败了 100.00% 的用户

内存消耗 : 42.3 MB , 在所有 Java 提交中击败了 100.00% 的用户

class Solution {
    public int search(int[] nums, int target) {
        int left =0,right = nums.length-1;
        int count = 0;
        while(left<right){
            int mid = (left+right)/2;
            if(nums[mid]>=target)
                right=mid;
            if(nums[mid]<target)
                left = mid+1;
        }
        while(left<nums.length&&nums[left++]==target)
            count++;
        return count;
    }
}

方法二：

ZHIPONGL1 （编辑过）2 天前双百。感觉二分法最重要的是mid，根据nums[mid]的各种情况来展开思考。

class Solution {
    public int search(int[] nums, int target) {
        int len = nums.length;
        int lo = 0, hi = len - 1;
        while (lo<=hi){
            int mid=lo+(hi-lo)/2;
            if(nums[mid]<target){
                lo=mid+1;
            }else if(nums[mid]>target){
                hi=mid-1;
            }else{
                if(nums[hi]!=target)
                    hi--;
                else if(nums[lo]!=target)
                    lo++;
                else
                    break;
            }
        }
        return hi-lo+1;
    }
}

方法三：

马保国

2020-09-01

大家都在用二分法和遍历，我看了题解基本都是二分法，我用了下双指针，其实效率不是很高，但是也是一种解法，给大家参考下，我水平不高，希望大家看看就好，我知道效率不咋高.谢谢大佬说出更优的代码

class Solution {
    public int search(int[] nums, int target) {
        if(nums.length == 0){
            return 0;
        }
        //这次使用双指针碰撞来玩
        int left = 0, right = nums.length - 1, count = 0;
        while (left <= right){
            if(nums[left] == target && nums[right] == target && left != right){
                //首先判断两个指针首尾的值是不是和要找的值一致，是就加2
                count += 2;
                left++;
                right--;
            } else if(nums[left] == target || nums[right] == target){
                //再判断 首尾只要有一个值和要找的值一致 + 1
                count ++;
                left++;
                right--;
            } else if(left == right && nums[left] == target){
                //这种情况是当你的数列个数为奇数时，最中间的那个是遍历不到的，所有这个循环条件是 left <= right
                count++;
                left++;
                right--;
            } else{
                //一个都没找到
                left++;
                right--;
            }
        }
        return count;
    }
}

方法四：

K神排序数组中的搜索问题，首先想到 二分法 解决。

作者：jyd
链接：https://leetcode-cn.com/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/solution/mian-shi-ti-53-i-zai-pai-xu-shu-zu-zhong-cha-zha-5/
来源：力扣（LeetCode）

class Solution {
    public int search(int[] nums, int target) {
        // 搜索右边界 right
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= target) i = m + 1;
            else j = m - 1;
        }
        int right = i;
        // 若数组中无 target ，则提前返回
        if(j >= 0 && nums[j] != target) return 0;
        // 搜索左边界 right
        i = 0; j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] < target) i = m + 1;
            else j = m - 1;
        }
        int left = j;
        return right - left - 1;
    }
}

以上代码显得比较臃肿（两轮二分查找代码冗余）。为简化代码，可将二分查找右边界 right 的代码** 封装至函数 helper() 。

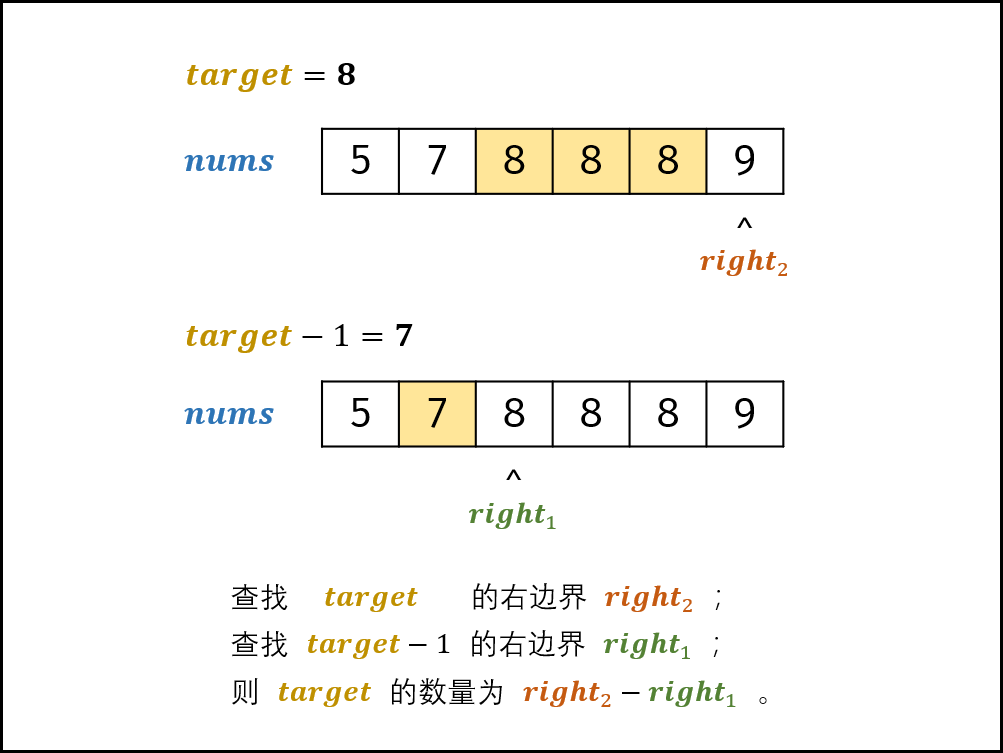
class Solution {
    public int search(int[] nums, int target) {
        return helper(nums, target) - helper(nums, target - 1);
    }
    int helper(int[] nums, int tar) {
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= tar) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}

【剑指Offer】个人学习笔记 53 - II. 0～n-1中缺失的数字

刷题日期：上午9:05 2021年5月16日星期日

个人刷题记录，代码收集，来源皆为leetcode

经过多方讨论和请教，现在打算往Java方向发力

主要答题语言为Java

题目：

剑指 Offer 53 - II. 0～n-1中缺失的数字

难度简单138

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

示例 1:

输入: [0,1,3]
输出: 2

示例 2:

输入: [0,1,2,3,4,5,6,7,9]
输出: 8

限制：

1 <= 数组长度 <= 10000

题目分析

也就是在数组中找第一值不等于下标的数。

初始解答：

先用二分

class Solution {
    public int missingNumber(int[] nums) {
        int l = 0, r = nums.length - 1; //初始化结果
		while(l < r){
			int m = (l + r) / 2;
			if(nums[m] == m){
				//比关键字大则关键字在左区域
				l = m + 1;
			}else {
				//比关键字小则关键字在右区域
				r = m;
			}
        }
        return l;
    }
}

执行结果：解答错误

显示详情添加备注

输入：[0]

输出：0

预期结果：1

这就很奇怪嗷，算是边界输入吧，评论里也有吐槽这种输入案例。

加入if也解决不了这个问题，又不用全部遍历的话，不知道往哪里改了。

参考了方法二，简单修改了while的条件和右边界缩小的范围，就跑出来了，还是自己分析不到位。

class Solution {
    public int missingNumber(int[] nums) {
        int l = 0, r = nums.length - 1; //初始化结果
		while(l <= r){
			int m = (l + r) / 2;
			if(nums[m] == m){
				//比关键字大则关键字在左区域
				l = m + 1;
			}else {
				//比关键字小则关键字在右区域
				r = m - 1;
			}
        }
        return l;
    }
}

执行结果：通过

显示详情添加备注

执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户

内存消耗：38.9 MB, 在所有 Java 提交中击败了58.01%的用户

学习他人：

方法一:

平海不平宁海平L1 2020-08-05

class Solution {
    public int missingNumber(int[] nums) {
        //计算出0-n的和  n*(n+1)/2
        int sum = nums.length * (nums.length+1)/2;
        return  sum - Arrays.stream(nums).sum() ;
    }
}

理论的和减去实际的和即为缺少的数字

方法二：

🌰L1 2021-02-22 简洁易懂的二分

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int i = 0, j = nums.size()-1;
        while(i <= j){
            int mid = i + (j - i)/2;
            if(nums[mid] != mid){
                j = mid - 1;
            }else{
                i = mid + 1;
            }
        }
        return i;
    }
}

方法三：

每天一题开胃菜 2021-05-02 100%

//已排序，使用双指针（对撞指针）
class Solution {
    public int missingNumber(int[] nums) {
        int left=0;
        int right=nums.length-1;
        int sum=nums.length;//两指针之和在不缺失情况下始终为n-1(这个n比输入数组长度大1)，即输入数组的长度
        while(left<=right){//left可以等于right，当不缺失情况下数组长度为奇数时
            int temp=nums[left]+nums[right];//生命周期只存在while循环内，并不算重复声明
            if(temp!=sum){
                return temp>sum?nums[left]-1:nums[right]+1;
            }
            left++;
            right--;
        }
        //由于nums一定缺失，所以理论上while循环内一定会出现temp!=sum，但有一种情况不会：当缺失的是最中间数字，如不缺失数组为[0,1,2,3,4]（不缺失数组一定是奇数个才有最中间数字），此时nums为[0,1,3,4]，每一对双指针仍然满足temp==sum
        return nums[(0+nums.length-1)/2]+1;
    }
}

方法四：

K神解题思路：

排序数组中的搜索问题，首先想到 二分法 解决。

作者：jyd
链接：https://leetcode-cn.com/problems/que-shi-de-shu-zi-lcof/solution/mian-shi-ti-53-ii-0n-1zhong-que-shi-de-shu-zi-er-f/
来源：力扣（LeetCode）

class Solution {
    public int missingNumber(int[] nums) {
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] == m) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}