浙大 PAT 甲级 1029 Median 中位数超时问题自拟测试点

最新推荐文章于 2022-08-11 11:51:10 发布

原创最新推荐文章于 2022-08-11 11:51:10 发布 · 808 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#归并排序 #PAT #浙大

PAT 专栏收录该内容

87 篇文章

订阅专栏

本文深入探讨PAT竞赛中一道涉及中位数计算的难题，详细解析如何在严格的内存限制下，利用归并排序思想高效处理大规模数据集，实现两组已排序数列的中位数查找。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

分析

这次的题目不是想象中的那么简单，看看通过率就知道了，我做的时候只有0.09，应该是目前通过率最低的一题。

难在哪里呢？好像不过就是将两组数读到数组或容器中，然后调用sort函数排序就行了，但这次真的要注意一下题目右边的限制条件了。嗯，念一下：

作者: CHEN, Yue

单位: 浙江大学

时间限制: 200 ms

内存限制: 1.5 MB

代码长度限制: 16 KB

内存限制到1.5M，每组数能到达200000个，肯定会内存超限。牛客网上的这题很宽松，开两个1000000的数组也没有任何问题。但是PAT上200000都会超限。另外，题目中说每个数限制在long int范围内，没有必要开辟成long型数组，会超限，整型数组就可以了，而且只能开辟一个。

内存只够开辟一个容纳200000个整型数的数组，但是又有两组数，那就限制了我们只能保存第一组数，第二组数边读取边处理。又看到两组数其实都是排好序了的，所以只要看过数据结构，总结过常用的几种排序方法，都肯定立马想到了归并排序。

下面截取《数据结构与算法分析——C语言描述》的内容稍微介绍一下归并排序。下面就是合并排序[1,13,24,26]和[2,15,27,38]这两个数组的过程。

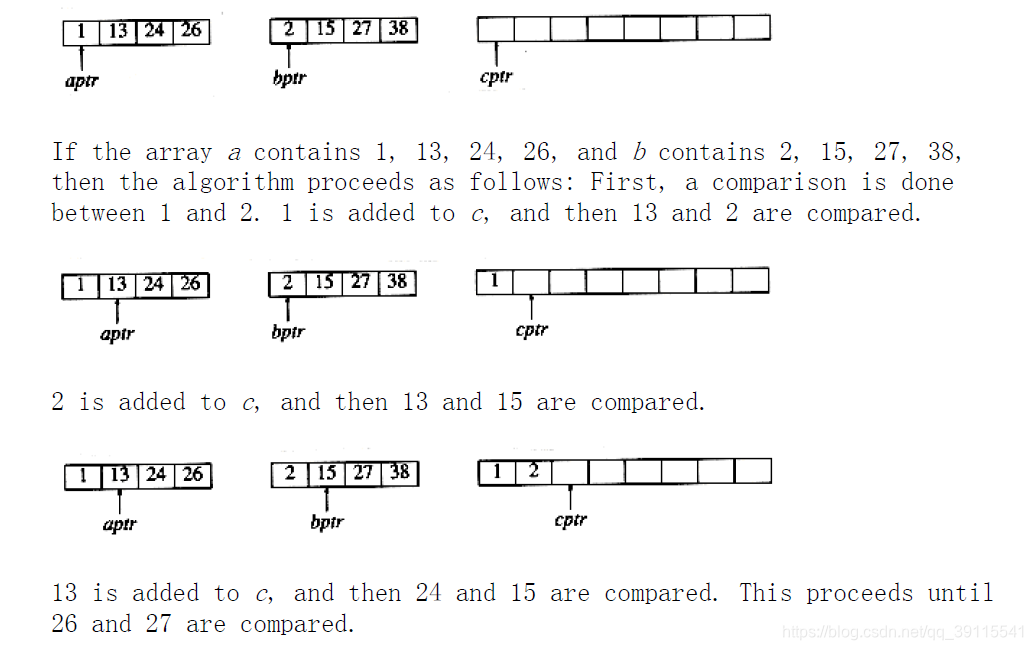
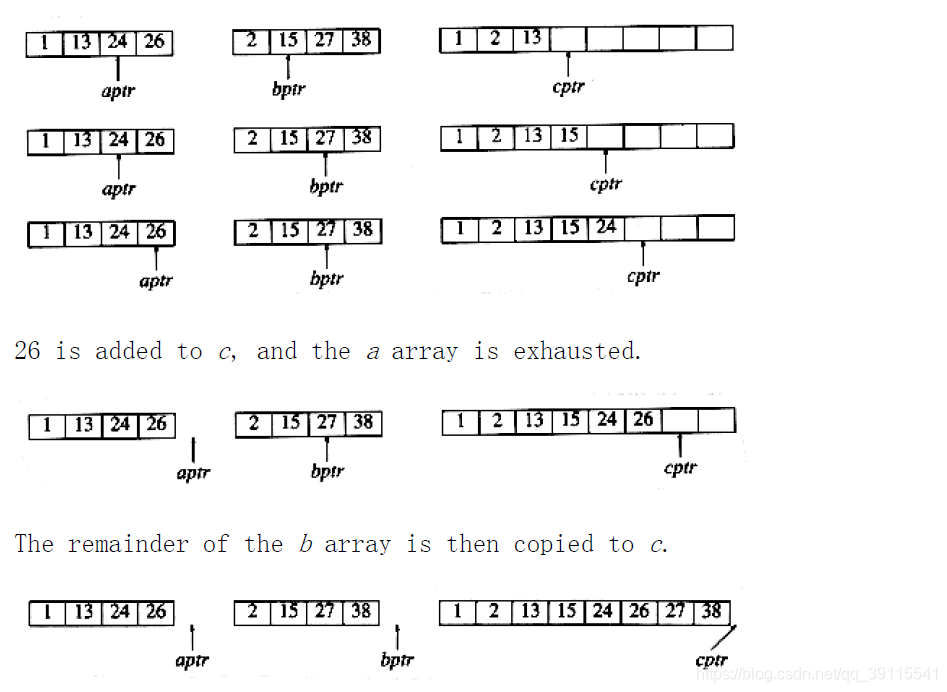
归并排序的思想就可以用在这题，当结果数组（也就是上图的第三个数组，图中只是显示出来方便展示过程，实际编码并不需要这第三个数组）装到第（n1+n2）/2和数字后就可以返回中位数了。在归并过程中，第二个数组也不需要开辟，只要边读边处理就行了。另外，当总数是偶数时，题目选取的是上中位数。

当在归并过程中，还没到中位数，但有一个数组提前遍历结束时，也是需要考虑的情况。

具体操作见以下代码。

代码

#include<stdio.h>

int l1[200000];

int main()
{
    int n1, n2;
    scanf("%d", &n1);
    for (int i = 0; i < n1; i++)
    {
        scanf("%d", &l1[i]);
    }
    scanf("%d", &n2);
    int median = (float)(n1 + n2) / 2.0 + 0.5;
    int ans;
    int i = 0, j = 0;
    int l2;
    scanf("%d", &l2);
    for (int k = 0; k < median; k++)
    {
        if (i == n1)
        {
            ans = l2;
            for (; j <= median - n1 - 2; j++)
            {
                scanf("%d", &ans);
            }
            break;
        }
        if (j == n2)
        {
            ans = l1[i + median - n2 - 1];
            break;
        }
        if (l1[i] <= l2)
        {
            i++;
            if (k == median - 1)
            {
                ans = l1[i - 1];
                break;
            }
        }
        else
        {
            j++;
            if (k == median - 1)
            {
                ans = l2;
                break;
            }
            if (j < n2)
            {
                scanf("%d", &l2);
            }
        }
    }
    printf("%d\n", ans);
    return 0;
}