反卷积

反卷积与空洞卷积详解

原创于 2019-04-21 16:17:21 发布 · 1.4k 阅读

8 ·

CC 4.0 BY-SA版权

深度学习专栏收录该内容

29 篇文章

订阅专栏

1. 反卷积：

参考地址：https://zhuanlan.zhihu.com/p/48501100
上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)，我们这里只讨论反卷积。这里指的反卷积，也叫转置卷积，它并不是正向卷积的完全逆过程，用一句话来解释：

反卷积是一种特殊的正向卷积，**先按照一定的比例通过补 0 来扩大输入图像的尺寸**，接着旋转卷积核，再进行正向卷积。
反卷积的数学推导

正向卷积的实现过程

假设输入图像 input 尺寸为 $\times 4$ ，元素矩阵为：
在这里插入图片描述

卷积核 kernel 尺寸为 $\times 3$ ，元素矩阵为：

$\begin{align*} input = \left[\begin{array}{cccccc} w_{0,0} & w_{0,1} & w_{0,2}\ w_{1,0} & w_{1,1} & w_{1,2}\ w_{2,0} & w_{2,1} & w_{2,2} \end{array}\right] \end{align*}$

步长 strides=1，填充 padding=0 ，即 i=4,k=3,s=1,p=0 ，

则按照卷积计算 $o=i−k+2ps+1o=\frac{i-k+2p}{s}+1$ 得到输出y为 $2×22\times2$ 大小的矩阵
把 input 的元素矩阵展开成一个列向量 X：
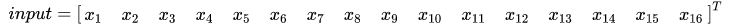
在这里插入图片描述
把输出图像 output 的元素矩阵展开成一个列向量 Y：

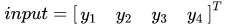
对于输入的元素矩阵 X 和输出的元素矩阵 Y ，用矩阵运算描述这个过程：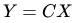

通过推导，我们可以得到稀疏矩阵 C
在这里插入图片描述
反卷积的操作就是要对这个矩阵运算过程进行逆运算，即通过 C 和 Y 得到 X ，根据各个矩阵的尺寸大小，我们能很轻易的得到计算的过程，即为反卷积的操作：

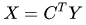
反卷积的输入输出尺寸关系
在进行反卷积时，简单来说，大体上可分为以下两种情况：
在这里插入图片描述
解释一下为什么要两种情况，看式子 $o=i−k+2ps+1o=\frac{i-k+2p}{s}+1$ 这里其实有两种情况，第一种 $\% s=0$ 第二种 $\% s！=0$ ，这个要在反卷积的时候体现出来
Relationship 1： $\% s=0$
输入输出尺寸关系：
$o = s (i - 1) - 2 p$
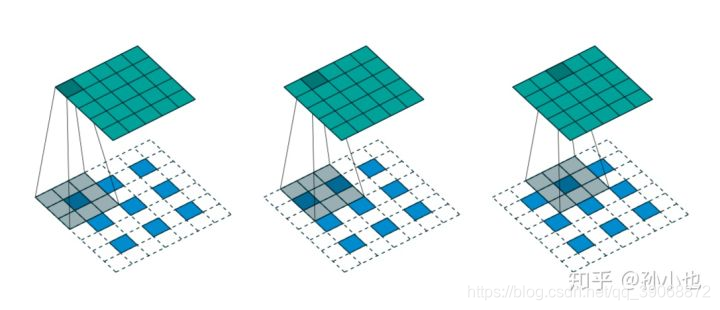
在这里插入图片描述
如上图所示，我们选择一个输入 input 尺寸为 $\times 3$ ，卷积核 kernel 尺寸为 $3×33\times 3$ ，步长 strides=2 ，填充 padding=1，即 i=3,k=3,s=2,p=1 ，则输出 output 的尺寸为 $o=2×(3−1)+3=5o=2\times(3-1)+3=5$ 。
Relationship 2： $\% s！=0$

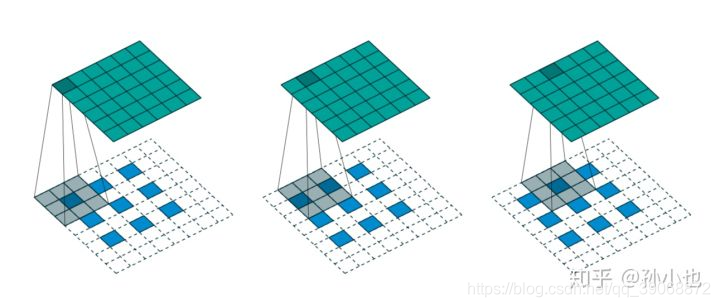
在这里插入图片描述

如上图所示，我们选择一个输入 input 的尺寸为 $\times 3$ ，卷积核 kernel 的尺寸为 $3×33\times 3$ ，步长 strides=2，填充 padding=1 ，即 i=3,k=3,s=2,p=1 ，则输出 output 的尺寸为 $o = 2 * (3 - 1) + 3 - 2 * 1 + 1 = 6$ 。
在 tensorflow 中实现反卷积
输入：
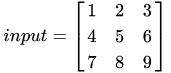
在这里插入图片描述
卷积核：

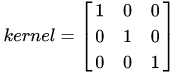
case1
如果要使输出的尺寸是 5*5 ，步数 stride=2 ，tensorflow 中的命令为：


transpose_conv = tf.nn.conv2d_transpose(value=input, 
                                       filter=kernel, 
                                       output_shape=[1,5,5,1], 
                                       strides=2, 
                                       padding='SAME')

当执行 transpose_conv 命令时，tensorflow 会先计算卷积类型、输入尺寸、步数和输出尺寸之间的关系是否成立，如果不成立，会直接提示错误，如果成立，执行如下操作：

现根据步数 strides 对输入的内部进行填充，这里 strides 可以理解成输入放大的倍数，即在 input 的每个元素之间填充 0 ，0 的个数 n 与 strides 的关系为：

n=strides-1

例如这里举例的 strides=2，即在 input 的每个元素之间填 1 个 0 ：
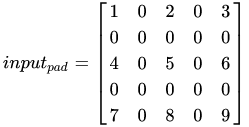
在这里插入图片描述
因为卷积类型为 same，所以此时， i=5,k=3,s=1,p=1 。

接下来，用卷积核 kernel 对填充后的输入 $input_{pad}$ 进行步长 stride=1 的正向卷积

case 2

我们将 case 1 中的输出尺寸 $output_{shape}$ 改成 6 ，其他参数均不变，tensorflow 中的命令为：

transpose_conv = tf.nn.conv2d_transpose(value=input,
filter=kernel,
output_shape=[1,6,6,1],
strides=2,
padding=‘SAME’)

卷积类型是 same，我们首先在外围填充一圈 0 ：
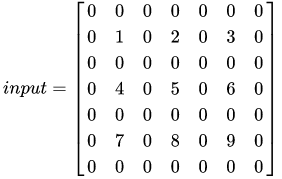
在这里插入图片描述
这时发现，填充后的输入尺寸与 $3×33\times3$ 的卷积核卷积后的输出尺寸是 5* 5 ，没有达到 output_shape 的 6* 6 ，这就需要继续填充 0，tensorflow 的计算规则是优先在左侧和上侧填充一排 0 ，填充后的输入变为：
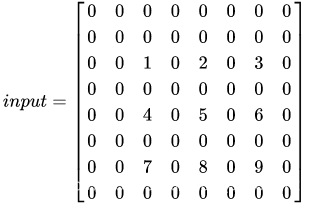
在这里插入图片描述

接下来，再对这个填充后的输入与 $3×33\times3$ 的卷积核卷积，结果为：
在这里插入图片描述

空洞卷积（Atrous Convolution)

在不做pooling损失信息和相同的计算条件下的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野，但计算资源有限而无法提高卷积核数量或大小时，可以考虑空洞卷积。
空洞卷积（dilated convolution）是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。利用添加空洞扩大感受野，让原本3x3的卷积核，在相同参数量和计算量下拥有5x5（dilated rate =2）或者更大的感受野，从而无需下采样。扩张卷积（dilated convolutions）又名空洞卷积（atrous convolutions），向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数，该参数定义了卷积核处理数据时各值的间距。换句话说，相比原来的标准卷积，扩张卷积（dilated convolution）多了一个hyper-parameter（超参数）称之为dilation rate（扩张率），指的是kernel各点之前的间隔数量，【正常的convolution 的 dilatation rate为 1】。
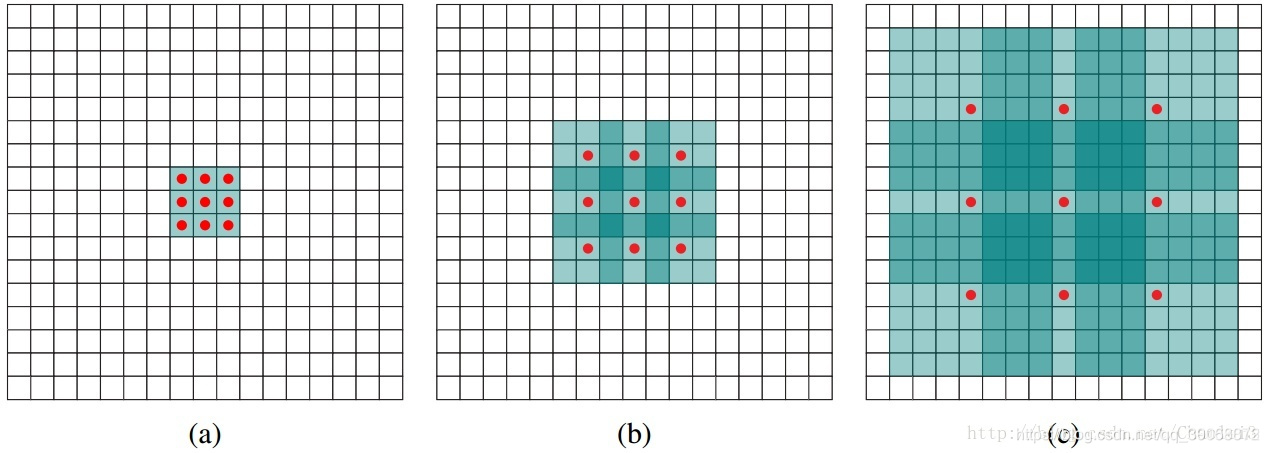
在这里插入图片描述
由上图可以看出来空洞卷积的意思，红色的点是原来卷积核中的点，绿色区域为添加的0，图（a）是dilatation rate=1（也就是原卷积核），图（b）是dilatation rate=2时，添加0的卷积核结果，图（c）是dilatation rate=4的结果。直观上来看，我们的卷积核需要训练的参数并没有增加，但是却降低了卷积后生成特征图的感受野。以（b）为例，如果输入的图片尺寸是 $a×aa\times a$ ，步长设置为1，经过（b）空洞卷积，得到的特征图的每一个点是由原图5x5的特征图产生，感受野变大很多。
假设原始卷积核大小为 $k$ ，空洞率为 $r$ ，经过空洞处理后卷积核大小为 $K$ ，则有关系
$K = k + (k - 1) * (r - 1)$
例如，假设原始 $K = 3 ， r = 2$ 则计算得到空洞后的卷积核大小为5，如果r=4，则得到的卷积核大小为9，分别对应图中的（b），（c）。

感受野的计算

1 卷积感受野的计算

从后往前计算
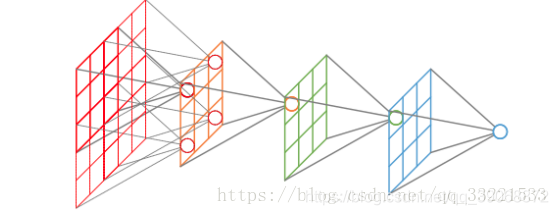在这里插入图片描述 $o u t p u t f i e l d s i z e = (i n p u t f i e l d s i z e - k e r n e l s i z e + 2 \times p a d d i n g) / s t r i d e + 1$
变形之后得到
$i n p u t f i e l d s i z e = （ o u t p u t f i e l d s i z e - 1 ） \times s t r i d e - 2 \times p a d d i n g + k e r n e l s i z e$ 。
因此可以通过后式从最后一层到第一次级联后计算在原图上的感受野。计算感受野时不需要考虑padding(因为我们不是在计算具体有边界的映射区域,而是计算抽象的大小),可以这样考虑，假设最后一层的输出大小是1，则前面一层的大小就是这个点相对于前一层的感受野，一直往前计算，得到第一层的大小，则第一层所有的点都对应于最后一层的那一个点，也就是感受野的大小，计算方式:

RF = 1 #待计算的feature map上的感受野大小 
for layer,stride,kernel_size in （top layer To down layer）:
#stride,kernel_size分别是对应的每一层的大小 　　
	RF = ((RF -1)* stride) + kernel size

从前向后计算
$lk=lk−1+((fk−1)∗∏i=1k−1si)l_k = l_{k-1} + ((f_k - 1) * \prod_{i=1}^{k-1}s_i)$
$l_k$ 是第k层的每个点的感受野, $f_k$ 是第k层卷积核的大小(宽或高, 并假设宽和高相等), $s_i$ 是第i层的卷积stride。
举个例子，第一层感受野 $l_1$ =1，第二层的卷积核 $f_2=3，stride s_2=1$ 第三层卷积核为5，步长是1，则第二层感受野
$l_2 = l_1+(f_2-1)*s_1=1+(3-1)*1=3$
第三层的感受野计算：
$l_3=l_2+(f_3-1)*s_1*s_2=3+(5-1)*1*1=7$
空洞卷积的感受野计算
如果知道了空洞卷积的计算方式，也知道了卷积感受野的计算方式，那么空洞卷积你也会了， $f_k^`$ 代表空洞卷积后的卷积核大小， $f_k$ 原始卷积核大小，上面已经分析过
$f_k^` =f_k + (f_k-1)*(r-1)$
只需要将 $f_k^`$ 带一每一个 $f_k$ 即可。
如果有三层CNN，分别为con3x3, dilation=1, conv3x3, dialation=2, conv3x3, dilation=5,它们的stried=1，则最后一层每个神经元的感受野为17x17.

空洞卷积存在的问题

问题 1

这个问题很直观，你想哈，原本3x3的卷积和你保持参数不变，在参数之间插0，这样不好的结果显而易见，会有很多像素点没有用到，这样会造成图像信息的流失，不是我们想要的

问题2

对于大物体，我们希望通过空洞卷积保持参数不增加的情况下扩大感受野，这样对大物体的识别会好，但是不能只考虑大物体啊，感受野扩大，直观的看，小物体的识别会受到影响

解决办法

通过叠加不同尺度的空洞卷积会对结果产生积极的影响，有人提出了**通向标准化设计：Hybrid Dilated Convolution (HDC)**不同于采用相同的空洞率的deeplab方案，该方案将一定数量的layer形成一个组，然后每个组使用连续增加的空洞率，其他组重复。如deeplab使用rate=2,而HDC采用r=1,r=2,r=3三个空洞率组合，这两种方案感受野都是13。但HDC方案可以从更广阔的像素范围获取信息，避免了grid问题。同时该方案也可以通过修改rate任意调整感受野。第一次空洞卷积rate=1，也就是不进行空洞操作，这样所有的像素点都会被考虑到。
HDC设计特性

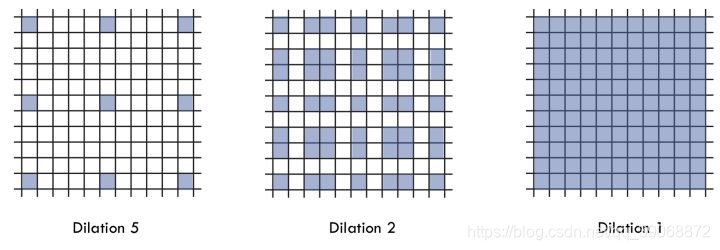
第一个特性是，叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积，依然会出现 gridding effect。
第二个特性是，我们将 dilation rate 设计成锯齿状结构，例如 [1, 2, 5, 1, 2, 5] 循环结构。
第三个特性是，我们需要满足一下这个式子：
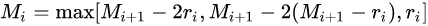
在这里插入图片描述
其中 $r_i$ 是 i 层的 dilation rate 而 $M_i$ 是指在 i 层的最大dilation rate，那么假设总共有n层的话，默认 $M_n=r_n$ 。假设我们应用于 kernel 为 k x k 的话，我们的目标则是 $M_2<k$ ，这样我们至少可以用 dilation rate 1 即 standard convolution 的方式来覆盖掉所有洞。一个简单的例子: dilation rate [1, 2, 5] with 3 x 3 kernel (可行的方案)