dfs---------吝啬的国度

吝啬的国度

时间限制： 1000 ms  |  内存限制： 65535 KB

难度： 3

描述

在一个吝啬的国度里有N个城市，这N个城市间只有N-1条路把这个N个城市连接起来。现在，Tom在第S号城市，他有张该国地图，他想知道如果自己要去参观第T号城市，必须经过的前一个城市是几号城市（假设你不走重复的路）。

输入

第一行输入一个整数M表示测试数据共有M(1<=M<=5)组
每组测试数据的第一行输入一个正整数N(1<=N<=100000)和一个正整数S(1<=S<=100000)，N表示城市的总个数，S表示参观者所在城市的编号
随后的N-1行，每行有两个正整数a,b(1<=a,b<=N)，表示第a号城市和第b号城市之间有一条路连通。

输出

每组测试数据输N个正整数，其中，第i个数表示从S走到i号城市，必须要经过的上一个城市的编号。（其中i=S时，请输出-1）

样例输入

1
10 1
1 9
1 8
8 10
10 3
8 6
1 2
10 4
9 5
3 7

样例输出

-1 1 10 10 9 8 3 1 1 8

我的思路：数据结构中的图的深度优先遍历，构造可达矩阵，1表示可达，-1表示自身，0表示不可达。如果v到t有路径，就输出v，如果没有，就深度遍历找v的可达路径，检测是否到t。

我的代码：

#include<iostream>
using namespace std;
void DFS(int v,int p[1000][1000],int t,int vis[1000]){
    vis[v]=1;
    for(int i=0;i<1000;i++){
        if(i==t){
            cout<<v+1<<ends;
            return ;
        }else if(p[v][i]>0&&vis[i]==0){
            DFS(v,p,t,vis);
        }
    }
}
int main(){
    int test;
    cin>>test;
    while(test--){
        int vis[1000];
    int p[1000][1000];


    for(int i=0;i<1000;i++){
        vis[i]=0;
       for(int j=0;j<1000;j++){
        if(i==j){
            p[i][j]=-1;
        }else{
            p[i][j]=0;
        }
       }
    }


    int n,s;
    cin>>n>>s;
    for(int i=0;i<n-1;i++){
        int a,b;
        cin>>a>>b;
        p[a-1][b-1]=1;
        p[b-1][a-1]=1;
    }
    for(int i=0;i<1000;i++){
        if(s-1==i){
            cout<<"-1"<<ends;
        }else{
            DFS(s-1,p,i,vis);
        }
    }


    }

}

emmm，结果错的，根本就没有走起来。

网上思路及代码（正确）：

分析

直接开数组 map[1000000][1000000]，可能会不过，用到了vector，利用其不定长。

头文件 #include<vector>

vector<int>a 就是一个不定长数组，类似于int a[]的整数数组，只不过他的长度不确定，可以用a.size()读取他的长度。

vector<int>a[max] 就是一个二维数组，只是第一维的大小是固定的（不超过max），二维的大小就不固定了.

尾部插入数字：vec.push_back(a);

刚开始看了网上代码也没懂，后来自己拿测试样例走了一遍才明白。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;

int M,N,S;
vector<int>map[100005]; //记录连通信息 
int pre[100005]; //记录每个节点的父亲节点 
int a,b;

void dfs(int x){
    
    for(int i=0; i<map[x].size(); i++){ //搜索所有与x相连的城市，即x的子节点 
    
        if(pre[map[x][i]]) //如果这个节点的pre已经被赋值，即已经找到父亲节点，就跳过，去找x的下一个子节点。 
            continue; 
            
        else{   //还没赋值，即还没找到父亲节点 
            pre[map[x][i]] = x; //x就是这个节点的父亲节点，因为是按照树的顺序依次乡下搜索的
            dfs(map[x][i]); //在我找个子节点的子节点 
        }       
    }   
}

int main()
{
    scanf("%d",&M);
    while(M--){
        
        memset(map, 0, sizeof(map));
        memset(pre, 0, sizeof(pre));
        scanf("%d%d",&N,&S);
        for(int i=0; i<N-1; i++){
            scanf("%d%d",&a, &b);
            map[a].push_back(b); //在 a 的连通城市中加上 b 
            map[b].push_back(a); //在 b 的连通城市中加上 a 
        }
        
        pre[S] = -1; //当前的起始城市没有父亲节点（因为是以他为最上方根节点构造树的） 
        dfs(S); //从当前城市开始搜索，为每个节点寻找父亲节点 
        
        for(int i=1; i<=N; i++) //打印每个节点的父亲节点，即从 S 到每个城市毕竟的上一个城市 
            cout<<pre[i]<<" ";  
    }
    
    return 0;
} 

理解了：

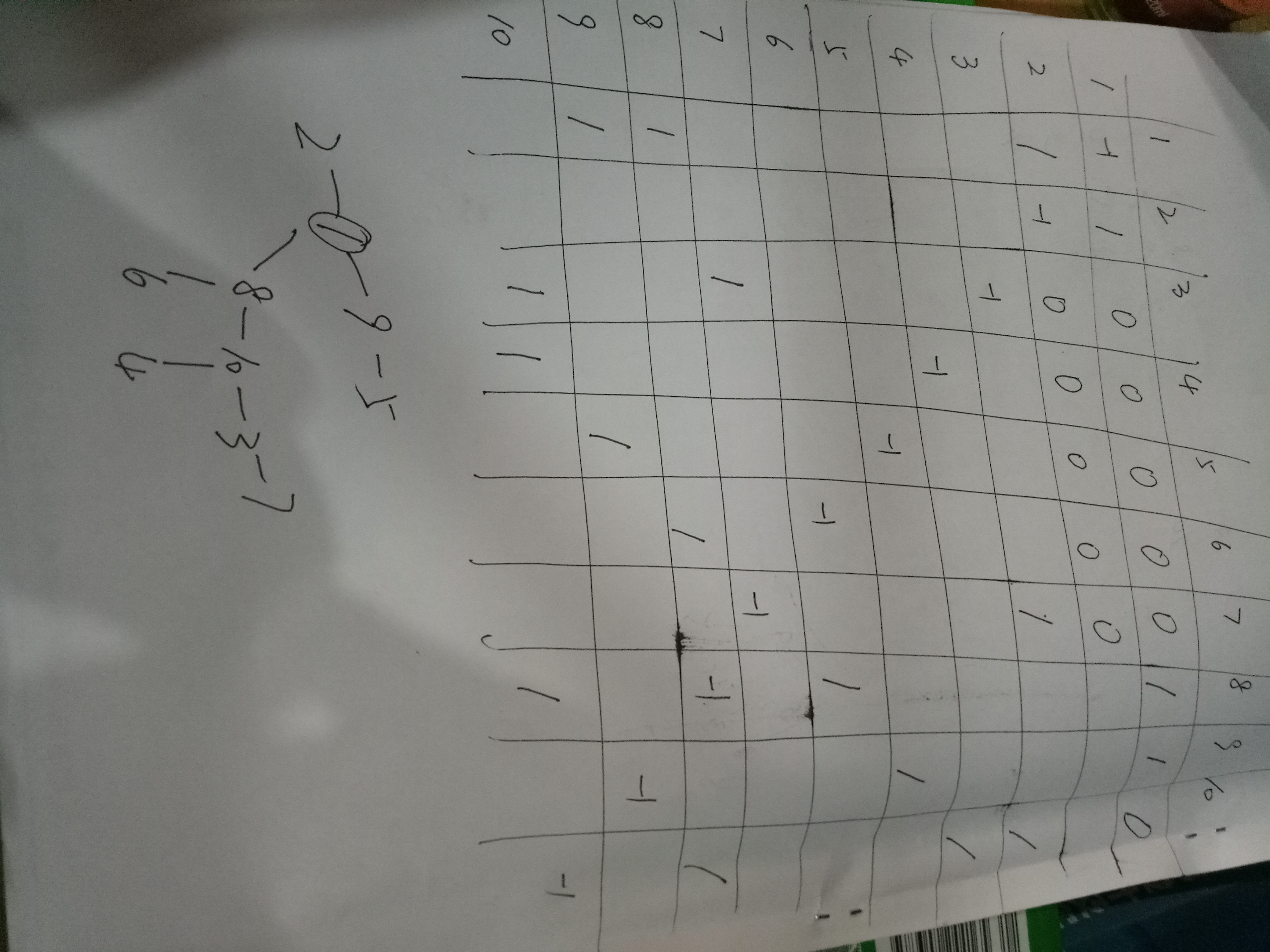
dfs得到父节点，可将图转换为树