排序算法总结(java)
冒泡排序
public static void BubbleSort(int array[]){
int t=0;
for (int i=0;i<array.length-1;i++){
for (int j=0;j<array.length-1;j++){
//比较相邻的两个元素,并且交换位置
if (array[j]>array[j+1]){
t=array[j];
array[j]=array[j+1];
array[j+1]=t;
}
}
}
}
选择排序
//选择排序
public static void selectSort(int array[]){
int t=0;
for(int i=0;i<array.length-1;i++){
int index=i;
//找到最小的元素
for (int j=i+1;j<array.length;j++){
if (array[index]>array[j]){
index=j;
}
}
if (index!=i){
t=array[i];
array[i]=array[index];
array[index]=t;
}
}
}
插入排序
//插入排序
public static void insertionSort(int[] ins){
for (int i=1;i<ins.length;i++){
for (int j=i;j>0;j--){
if (ins[j]<ins[j-1]){
int temp=ins[j-1];
ins[j-1]=ins[j];
ins[j]=temp;
}
}
}
}
快速排序
//快速排序
public static void quickSort(int array[],int start,int end){
if (start>=end){
return;
}
//定义基准值
int pivot=array[start];
//开始的下标位置
int i=start;
//结束的下标位置
int j=end;
while (i<j){
while (i<j && array[j]>=pivot){
j--;
}
while (i<j && array[i]<=pivot){
i++;
}
if (i<j){
int temp=array[j];
array[j]=array[i];
array[i]=temp;
}
}
//将pivot移动到相应位置上
array[start]=array[i];
array[i]=pivot;
quickSort(array,start,i-1);
quickSort(array,i+1,end);
}
希尔排序
希尔排序(Shell Sort)是插入排序的一种,它是针对直接插入排序算法的改进。
希尔排序又称缩小增量排序,因 DL.Shell 于 1959 年提出而得名。
它通过比较相距一定间隔的元素来进行,各趟比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一趟排序为止。
过程示意图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AZlqpvUz-1654771833868)(https://gitee.com/mengyuw20/cloudimage/raw/master/img/image-20220607162525636.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fw03J3HI-1654771833870)(C:\Users\mengyuw\AppData\Roaming\Typora\typora-user-images\image-20220607162603347.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RXBCU1ir-1654771833873)(https://gitee.com/mengyuw20/cloudimage/raw/master/img/image-20220607162627338.png)]
代码
//希尔排序
public static void shellSort(int[] arr){
for (int step=arr.length/2;step>0;step/=2){
for (int i=step;i<arr.length;i++){
int value=arr[i];
int j;
for (j=i-step;j>=0 && arr[j]>value;j-=step){
arr[j+step]=arr[j];
}
arr[j+step]=value;
}
}
}
归并排序
//归并排序
public static void mergeSort(int[] arr,int left,int right){
if (right-left<=1){
return;
}
//将区间一分为二
int mid=(left+right)/2;
mergeSort(arr,left,mid);
mergeSort(arr,mid,right);
merge(arr,left,mid,right);
}
//merge的功能是将两个本身有序的数组合并成一个有序数组
//合并的两个数组为
//[left,mid)
//[mid,right)
public static void merge(int[] arr,int left,int mid,int right){
//创建一个临时数组,用来存放合并的结果
//这个数组应该可以存放合并后的结果
int[] tmp=new int[right-left];
//当前要把新的数组元素放到tmp数组的哪个下标上
int tmpSize=0;
int l=left;
int r=mid;
while (l<mid && r<right){
//判断两个有序数组的第一个元素谁小
if (arr[l]<=arr[r]){
tmp[tmpSize]=arr[l];
tmpSize++;
l++;
}else {
//arr[r]小,就将它放在首位
tmp[tmpSize]=arr[r];
tmpSize++;
r++;
}
}
//如果其中的一个数组遍历完了,就把另一个数组的剩余部分拷贝到临时空间
while (l<mid){
//如果l<mid剩下的就都是[left,mid)这个数组
tmp[tmpSize]=arr[l];
tmpSize++;
l++;
}
while (r<right){
//剩下的为[mid,right)这个数组
tmp[tmpSize]=arr[r];
tmpSize++;
r++;
}
//最后一步,再把临时空间的内容都拷贝回参数数组
//拷贝的是[left,right),这个可能不是从0开始的
for (int i=0;i<tmp.length;i++){
arr[left+i]=tmp[i];
}
}
堆排序
堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
什么是堆
堆是一个树形结构,其实堆的底层是一棵完全二叉树。而完全二叉树是一层一层按照进入的顺序排成的。按照这个特性,我们可以用数组来按照完全二叉树实现堆。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hqaNKVK4-1654771833874)(https://gitee.com/mengyuw20/cloudimage/raw/master/img/image-20220608110403566.png)]
大顶堆与小顶堆
大顶堆原理:根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最大者,称为大顶堆。大顶堆要求根节点的关键字既大于或等于左子树的关键字值,又大于或等于右子树的关键字值。
小顶堆原理:根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最小者,称为小顶堆。小堆堆要求根节点的关键字既小于或等于左子树的关键字值,又小于或等于右子树的关键字值。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UOClfp4H-1654771833875)(https://gitee.com/mengyuw20/cloudimage/raw/master/img/image-20220608110850402.png)]
堆排序思想
- 构建初始堆,将待排序列构成一个大顶堆(或者小顶堆),升序大顶堆,降序小顶堆;
- 将堆顶元素与堆尾元素交换,并断开(从待排序列中移除)堆尾元素。
- 重新构建堆。
- 重复2~3,直到待排序列中只剩下一个元素(堆顶元素)。
图解
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C9gG2Uzl-1654771833876)(https://gitee.com/mengyuw20/cloudimage/raw/master/img/image-20220608140121318.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1woM5G0N-1654771833876)(https://gitee.com/mengyuw20/cloudimage/raw/master/img/image-20220608140210112.png)]
代码
public static void heapSort(int[] arr){
//创建堆
for (int i=(arr.length-1)/2;i>=0;i--){
//从第一个非叶子节点从下至上,从右至左调整结构
adjustHeap(arr,i,arr.length);
}
//调整堆结构+交换堆顶元素与末尾元素
for (int i=arr.length-1;i>0;i--){
//将堆顶元素与末尾元素进行交换
int temp=arr[i];
arr[i]=arr[0];
arr[0]=temp;
//重新对堆进行调整
adjustHeap(arr,0,i);
}
}
public static void adjustHeap(int[] arr, int parent, int length) {
//将temp作为父节点
int temp = arr[parent];
//左孩子
int lChild = 2 * parent + 1;
//循环条件为有左孩子
while (lChild < length) {
//右孩子
int rChild = lChild + 1;
// 如果有右孩子结点,并且右孩子结点的值大于左孩子结点,则选取右孩子结点
if (rChild < length && arr[lChild] < arr[rChild]) {
lChild++;
}
// 如果父结点的值已经大于孩子结点的值,则直接结束
if (temp >= arr[lChild]) {
break;
}
// 把孩子结点的值赋给父结点
arr[parent] = arr[lChild];
//选取孩子结点的左孩子结点,继续向下筛选
parent = lChild;
lChild = 2 * lChild + 1;
}
arr[parent] = temp;
}
计数排序
public static int[] CountSort(int[] nums){
if (nums.length==0) return nums;
//寻找数组中的最大值,最小值
//bias:偏移量,用以定位原始数组每个元素在计数数组中的下标位置
int bias,min=nums[0],max=nums[0];
for (int i=1;i<nums.length;i++){
if (nums[i]>max){
max=nums[i];
}
if (nums[i]<min)
min=nums[i];
}
bias=0-min;
//获得计数数组的容量
int[] counterArray=new int[max-min+1];
Arrays.fill(counterArray,0);
//遍历整个原始数组,将原始数组中每个元素值转化为计数数组下标,并将计数数组下标对应的元素值大小进行累加
for (int i=0;i<nums.length;i++){
counterArray[nums[i]+bias]++;
}
//访问原始数组时的下标计数器
int index=0;
//访问计数数组时的下标计数器
int i=0;
while (index<nums.length){
//只要计数数组中当前下标元素不为零,就将计数数组中的元素转换后,重新写回原始数组
if (counterArray[i]!=0){
nums[index]=i-bias;
counterArray[i]--;
index++;
}else
i++;
}
return nums;
}
桶排序
//桶排序是改进的计数排序,将区间分为几个桶,并且将桶内的数据排序,再将各个桶合并
public static ArrayList<Integer> sort(ArrayList<Integer> array,int bucketCap){
if (array==null || array.size()<2)
return array;
int max=array.get(0),min=array.get(0);
//找到最大值和最小值
for (int i=0;i<array.size();i++){
if (array.get(i)>max){
max=array.get(i);
}
if (array.get(i)<min){
min=array.get(i);
}
}
//计算桶的数量
int bucketCount=(max-min)/bucketCap+1;
//构建桶
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketCount);
ArrayList<Integer> resultArr=new ArrayList<>();
for (int i=0;i<bucketCount;i++){
bucketArr.add(new ArrayList<Integer>());
}
//将原始数组中的数据分配到桶中
for (int i=0;i<array.size();i++){
bucketArr.get((array.get(i)-min)/bucketCap).add(array.get(i));
}
for (int i=0;i<bucketCount;i++){
if (bucketCap==1){
for (int j=0;j<bucketArr.get(i).size();j++){
resultArr.add(bucketArr.get(i).get(j));
}
}else {
if (bucketCount==1) {
bucketCap--;
}
//对桶中的数据再次使用桶排序
ArrayList<Integer> temp=sort(bucketArr.get(i),bucketCap);
for (int j=0;j<temp.size();j++){
resultArr.add(temp.get(j));
}
}
}
return resultArr;
}
基数排序
//基数排序
public static int[] radixSort(int[] nums){
if (nums==null || nums.length<2)
return nums;
//找出最大数
int max=nums[0];
for (int i=1;i<nums.length;i++){
max=Math.max(max,nums[i]);
}
//先算出最大数的位数,它决定了需要进行几轮排序
int maxDigit=0;
while (max!=0){
max/=10;
maxDigit++;
}
int mod=10,div=1;
//构建桶
ArrayList<ArrayList<Integer>> bucketList=new ArrayList<ArrayList<Integer>>();
for (int i=0;i<10;i++){
bucketList.add(new ArrayList<Integer>());
}
//按照从右往左的顺序,依次将每一位都当作一次关键字,然后按照关键字对数组排序,每一轮排序都基于上一轮排序的结果
for (int i=0;i<maxDigit;i++,mod*=10,div*=10){
//遍历原始数组,放入桶中
for (int j=0;j<nums.length;j++){
int num=(nums[j]%mod)/div;
bucketList.get(num).add(nums[j]);
}
//桶中的数据写回原数组,清除桶,准备下一轮的排序
int index=0;
for (int j=0;j<bucketList.size();j++){
for (int k=0;k<bucketList.get(j).size();k++){
nums[index++]=bucketList.get(j).get(k);
}
bucketList.get(j).clear();
}
}
return nums;
}
排序算法时间复杂度总结
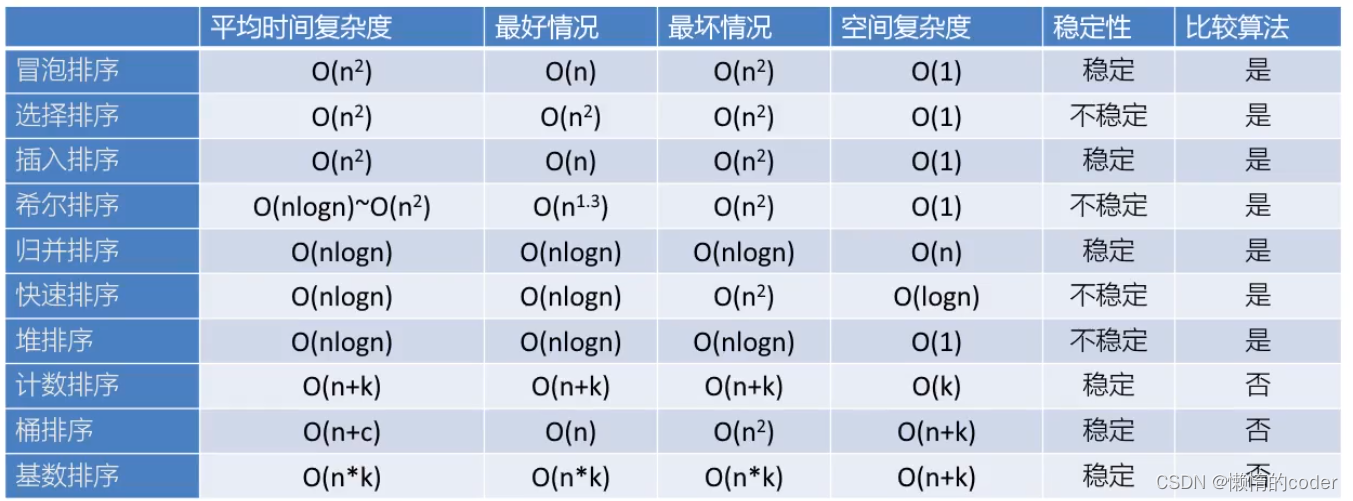







 本文详细介绍了Java中常见的五种排序算法:冒泡排序、选择排序、插入排序、快速排序和归并排序,包括它们的工作原理、代码实现及时间复杂度分析。此外,还提及了希尔排序、堆排序、计数排序、桶排序和基数排序等其他排序算法,帮助读者深入理解排序算法的多样性及其应用场景。
本文详细介绍了Java中常见的五种排序算法:冒泡排序、选择排序、插入排序、快速排序和归并排序,包括它们的工作原理、代码实现及时间复杂度分析。此外,还提及了希尔排序、堆排序、计数排序、桶排序和基数排序等其他排序算法,帮助读者深入理解排序算法的多样性及其应用场景。

















 1051
1051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










