20190722杭电多校第一场

原创 于 2019-07-27 01:40:29 发布 · 403 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#杭电多校

本文精选了多道算法竞赛题目，包括贪心算法、动态规划、网络流等，提供了详细的解题思路和AC代码，适合算法爱好者和竞赛选手学习参考。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

1001 Blank （补题 By wtw）

https://www.cnblogs.com/intwentieth/p/11262363.html

1002 Operation（补题 By jlz）

贪心的维护多个线性基，类似codeforces 1100F，具体思路可以参考下面的博客。

某大神博客

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
#define ll long long
#define p_b push_back
#define db double
const int INF=0x3f3f3f3f;
int T,n,m;
int pos[31][maxn],d[31][maxn],x;
void add(int x,int p){
	int r=p;
	for(int i=30;i>=0;i--){
		if(x&(1<<i)){
			if(!d[i][r]){
				d[i][r]=x,pos[i][r]=p;
				break;
			}
			if(pos[i][r]<p) swap(d[i][r],x),swap(pos[i][r],p);
			x^=d[i][r];
		}
	}
}
int query(int l,int r){
	int res=0;
	for(int i=30;i>=0;i--) if(pos[i][r]>=l&&(res^d[i][r])>res) res^=d[i][r];
	return res;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	scanf("%d",&T);
	while(T--){
		scanf("%d %d",&n,&m);
		for(int i=1;i<=n;i++){
			scanf("%d",&x);
			for(int j=0;j<=30;j++) d[j][i]=d[j][i-1],pos[j][i]=pos[j][i-1];
			add(x,i);
		}
		int op,l,r,ans=0;
		for(int i=1;i<=m;i++){
			scanf("%d",&op);
			if(op==0){
				scanf("%d %d",&l,&r);
				l=(l^ans)%n+1,r=(r^ans)%n+1;
				if(l>r) swap(l,r);
				ans=query(l,r);
				cout<<ans<<"\n";
			}
			else{
				scanf("%d",&x);
				x=(x^ans);
				n=n+1;
				for(int j=0;j<=30;j++) d[j][n]=d[j][n-1],pos[j][n]=pos[j][n-1];
				add(x,n);
			}
		}
	}
	return 0;
}

1003 Milk （待补）

1004 Vacation （Solved By cys、补题 By jlz）

没想到是一道脑洞题，队友似乎是维护运动状态模拟过去的。

做法很多，这里讲两种比较好写的。

O(nlogn):二分时间，维护每辆车的结束位置，check最后一辆车能否通过终点;

O(n):求出每辆车到达对应的某个位置花费的时间，取最大值即为答案。理由如下：

仅补了O(n)做法的代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
#define ll long long
#define p_b push_back
const int INF=0x3f3f3f3f;
int n,s[maxn],v[maxn],l[maxn];
int main(){
//	freopen("in.txt","r",stdin);
	while(~scanf("%d",&n)){
		for(int i=0;i<=n;i++) scanf("%d",&l[i]);
		for(int i=0;i<=n;i++) scanf("%d",&s[i]);
		for(int i=0;i<=n;i++) scanf("%d",&v[i]);
		double ans=s[0]*1.0/v[0];
		int d=0;
		for(int i=1;i<=n;i++){
			d+=l[i];
			ans=max(ans,(s[i]+d)*1.0/v[i]);
		}
		printf("%.10f\n",ans);
	}
	return 0;
}

1005 Path （Solved By jlz/wtw）

求出最短路径图然后网络流求最小割即可。

有的同学不太理解如何建出最短路径图，一个比较简单的方法是在迪杰斯特拉求最短路过程中就存下反向边。

最短路径图部分由我完成，最小割部分由队友完成，可能是板子习惯问题，他拿着我建好的图再建了一遍图。。。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e4+5;
#define ll long long
#define p_b push_back
const int INF=0x3f3f3f3f;
struct node{
	int v;
	ll w;
	node(int _v=0,ll _w=0):v(_v),w(_w){}
	bool operator<(const node &b)const{
		return w>b.w;
	}
};
ll ans;
int x,y,c;
vector<node> G[maxn],E[maxn];//G存反向的最短路径图，E为原图 
int TT,n,m,s=1,ed;
ll dis[maxn];
bool vis[maxn];
priority_queue<node> pq;
bool dij(){
	memset(dis,INF,sizeof(dis));
	memset(vis,0,sizeof(vis));
	dis[s]=0;
	pq.push(node(s,0));
	bool f=0;//f用来判是否1到n联通 
	while(!pq.empty()){
		node u=pq.top();
		pq.pop();
		if(u.v==ed){
			f=1;break;
		}
		if(vis[u.v]) continue;
		vis[u.v]=1;
		for(node tt:E[u.v]){
			if(vis[tt.v]) continue;
			if(dis[tt.v]>dis[u.v]+tt.w){
				dis[tt.v]=dis[u.v]+tt.w;
				G[tt.v].clear();
				G[tt.v].p_b(node(u.v,tt.w));
				pq.push(node(tt.v,dis[tt.v]));
			}
			else if(dis[tt.v]==dis[u.v]+tt.w){
				G[tt.v].p_b(node(u.v,tt.w));
			}
		}
	}
	while(!pq.empty()) pq.pop();
	return f;
}
struct Line{int v,next;ll w;}e[maxn];
int h[maxn],cnt=2;
inline void Add(int u,int v,ll w)
{
    e[cnt]=(Line){v,h[u],w};h[u]=cnt++;
    e[cnt]=(Line){u,h[v],0};h[v]=cnt++;
}
int level[maxn],S,T;
bool bfs()
{
    memset(level,0,sizeof(level));level[S]=1;
    queue<int> Q;Q.push(S);
    while(!Q.empty())
    {
        int u=Q.front();Q.pop();
        for(int i=h[u];i;i=e[i].next)
            if(e[i].w&&!level[e[i].v])
                level[e[i].v]=level[u]+1,Q.push(e[i].v);
    }
    return level[T];
}
ll dfs(int u,ll flow)
{
    if(u==T||!flow)return flow;
    ll ret=0;
    for(int i=h[u];i;i=e[i].next)
        if(e[i].w&&level[e[i].v]==level[u]+1)
        {
            ll d=dfs(e[i].v,min(flow,e[i].w));
            ret+=d;flow-=d;
            e[i].w-=d;e[i^1].w+=d;
        }
    if(!ret)level[u]=0;
    return ret;
}
ll Dinic()
{
    ll ret=0;
    while(bfs())ret+=dfs(S,INF);
    return ret;
}
int main(){
//	freopen("in.txt","r",stdin);
	scanf("%d",&TT);
	while(TT--){
        cnt=2;
        memset(h,0,sizeof(h));
		ans=1e18;
		scanf("%d %d",&n,&m);
		s=1,ed=n;
		for(int i=1;i<=m;i++){
			scanf("%d %d %d",&x,&y,&c);
			E[x].p_b(node(y,c));
		}
		if(!dij()) cout<<"0\n";
		else{
			s=n,ed=1;
            S=n,T=1;
            for(int i=n;i>=1;i--){
                for(node tt:G[i]){
                    Add(i,tt.v,tt.w);
                }
            }
            cout<<Dinic()<<"\n";
		}
		for(int i=1;i<=n;i++) G[i].clear(),E[i].clear();
	}
	return 0;
}

1006 Typewriter （补题 By wtw）

https://www.cnblogs.com/intwentieth/p/11262363.html

1007 Meteor （待补）

1008 Desert （待补）

1009 String （Solved By jlz）

首先检查一遍是否有解，需要判断每种字符个数是否大于需求的最小值、所有字符最小值的和是否大于k、所有字符最大值的和是否小于k。

若确定有解，预处理出原串中每种字符个数的后缀和，并且用vector维护每种字符在原串的位置序列。（因为可以做到每个位置只看一次，用队列维护位置序列也可以。）

从前往后从'a'到'z'贪心枚举k个位置的字符，若某种字符满足：

1、该种字符还没选完且在原串位置比前面选过的字符位置大；2、该种字符个数还没选到最大值；3、选了该种字符后所有字符的个数（即后缀和）仍然可以保证满足最小值；4、最小值的和仍然小于等于未枚举的位置数。

则说明该位置为这种字符。

判断1可通过维护的位置序列，判断2可通过更新每种字符要选的最大值，判断3可通过后缀和，判断4可通过更新每种字符要选的最小值。

最坏复杂度O(26*26*k)，但感觉上应该会比这个低不少。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
#define ll long long
#define p_b push_back
const int INF=0x3f3f3f3f;
char str[maxn],ans[maxn]; 
vector<int> v[26]; 
int k,l[26],r[26];
int sum[30][maxn];
int main(){
//	freopen("in.txt","r",stdin);
	while(scanf("%s %d",str,&k)!=EOF){
		int mins=0,maxs=0;
		for(int i=0;i<26;i++) scanf("%d %d",&l[i],&r[i]),mins+=l[i],maxs+=r[i];
		int len=strlen(str),cnt=0;
		for(int i=0;i<26;i++) sum[i][len]=0;
		for(int i=len-1;i>=0;i--){
			for(int j=0;j<26;j++){
				sum[j][i]=sum[j][i+1]+(j==str[i]-'a');
			}
		}
		bool f=0;
		for(int i=0;i<26;i++){
			if(sum[i][0]<l[i]){
				f=1;break;
			}
		}
		if(mins>k||maxs<k) f=1;
		if(f){
			puts("-1");continue;
		}
		for(int i=0;i<len;i++){
			v[str[i]-'a'].p_b(i);
		}
		int pre=-1,tmp,now;
		for(int i=0;i<k;i++){
			tmp=-1;
			for(int j=0;j<26;j++){
				f=0;
				now=upper_bound(v[j].begin(),v[j].end(),pre)-v[j].begin();
				if(now==sum[j][0]||r[j]==0) continue;
				mins=0;
				now=v[j][now];
				for(int tt=0;tt<26;tt++){
					if(sum[tt][now]<l[tt]){
						f=1;break;
					}
					if(tt==j) mins+=max(l[tt]-1,0);
					else mins+=l[tt];
				}
				if(mins>k-i-1) f=1;
				if(!f){
					pre=now,tmp=j;break;
				}
			}
			ans[i]=tmp+'a';
			l[tmp]--,r[tmp]--;
			l[tmp]=max(l[tmp],0);
		}
		ans[k]='\0';
		cout<<ans<<"\n";
		for(int i=0;i<26;i++) v[i].clear();
	}
	return 0;
}

1010 Kingdom （补题 By wtw）

https://www.cnblogs.com/intwentieth/p/11262363.html

1011 Function（补题 By jlz）

求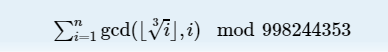

看题解之前自己想了很久很久，令m=\left \lfloor n^{\frac{1}{3}} \right \rfloor，只能想到转化为 \sum_{i=m^{3}}^{n}gcd(m,i)+ \sum_{i=1}^{m-1}\sum_{j=i^{3}}^{(i+1)^3-1}gcd(i,j)。然后就不会了，看了题解也无法理解。

还好我们有dls讲题！

dls开场就讲了这题需要用到gcd(x,y)=\sum_{d|x,d|y}\varphi (d)，并说这是常用的式子。（窝见过的东西确实太少了QAQ

实际含义是两个数的gcd的值等于两个数所有公因子的欧拉函数值之和。

并且可得

                              \sum_{i=l}^{r}gcd(x,i)=\sum_{i=l}^{r}\sum_{d|x,d|i}\varphi(d)=\sum_{d|x}\varphi(d)*(\left \lfloor \frac{r}{d} \right \rfloor-\left \lfloor \frac{l-1}{d} \right \rfloor)

推出的最后那部分相当于是先枚举x的因子，然后得到该因子在区间[l,r]的倍数的个数，可知与原式等价。

知道了这个式子，这道题就容易解决了。

预处理，先通过线性筛O(n)得到欧拉函数，用两个数组分别维护\varphi(d)的前缀和与\varphi(d)*d的前缀和。

对于

        \sum_{i=m^{3}}^{n}gcd(m,i)+ \sum_{i=1}^{m-1}\sum_{j=i^{3}}^{(i+1)^3-1}gcd(i,j)

首先考虑式子的前半部分，可得

                                     \sum_{i=m^{3}}^{n}gcd(m,i)=\sum_{i=m^{3}}^{n}\sum_{d|m,d|i}\varphi(d)=\sum_{d|m}\varphi(d)*(\left \lfloor \frac{n}{d} \right \rfloor - \left \lfloor \frac{m^{3}-1}{d} \right \rfloor )

欧拉函数已知，枚举m的因子，显然可以在O(\sqrt m)时间复杂度求出。

再考虑第二部分，方便起见令k=m-1，则为

                                                                    \sum_{i=1}^{k}\sum_{j=i^{3}}^{(i+1)^3-1}gcd(i,j)

首先有

            \sum_{j=i^{3}}^{(i+1)^3-1}gcd(i,j)=\sum_{d|i}\varphi(d)*(\left \lfloor \frac{(i+1)^{3}-1}{d} \right \rfloor - \left \lfloor \frac{i^{3}-1}{d} \right \rfloor)

因为d|i，所以

    (\left \lfloor \frac{(i+1)^{3}-1}{d} \right \rfloor - \left \lfloor \frac{i^{3}-1}{d} \right \rfloor)=(\frac{i^{3}+3*i^{2}+3*i}{d} - (\frac{i^{3}}{d} - 1))\\= ( \frac{3*i^{2}}{d} + \frac{3*i}{d} + 1)

所以

       \sum_{i=1}^{k}\sum_{j=i^{3}}^{(i+1)^3-1}gcd(i,j)=\sum_{i=1}^{k}\sum_{d|i}\varphi(d)*( \frac{3*i^{2}}{d} + \frac{3*i}{d} + 1) \\=\sum_{i=1}^{k}\sum_{d|i}\varphi(d)+3*\sum_{i=1}^{k}\sum_{d|i}\varphi(d)*( \frac{i^{2}}{d} + \frac{i}{d}) \\=\sum_{i=1}^{k}i+ 3*\sum_{d=1}^{k}\varphi(d)*\sum_{d|i}( \frac{i^{2}}{d} + \frac{i}{d} ) \\=\frac{k*(k+1)}{2}+3*\sum_{d=1}^{k}\varphi(d)*\sum_{j=1}^{\left \lfloor \frac{k}{d} \right \rfloor}( \frac{(j*d)^{2}}{d} + \frac{(j*d)}{d}) \\=\frac{k*(k+1)}{2}+3*\sum_{d=1}^{k}\varphi(d)*\sum_{j=1}^{\left \lfloor \frac{k}{d} \right \rfloor}( d*j^{2} + j)

后面那部分又可以变为

                                    3*\sum_{d=1}^{k}\varphi(d)*\sum_{j=1}^{\left \lfloor \frac{k}{d} \right \rfloor}( d*j^{2} + j)=3*\sum_{d=1}^{k}\varphi(d)*d*\sum_{j=1}^{\left \lfloor \frac{k}{d} \right \rfloor}j^{2} +3*\sum_{d=1}^{k}\varphi(d)*\sum_{j=1}^{\left \lfloor \frac{k}{d} \right \rfloor}j\\=\sum_{d=1}^{k}\varphi(d)*d*\frac{\left \lfloor \frac{k}{d} \right \rfloor *(\left \lfloor \frac{k}{d} \right \rfloor+1)*(2*\left \lfloor \frac{k}{d} \right \rfloor+1)}{2}+3*\sum_{d=1}^{k}\varphi(d)*\frac{\left \lfloor \frac{k}{d} \right \rfloor *(\left \lfloor \frac{k}{d} \right \rfloor+1)}{2}

因为预处理了\varphi(d)的前缀和与\varphi(d)*d的前缀和，可以利用整除分块求上式，时间复杂度O(\sqrt k)。（因为k=m-1,即O(\sqrt m)）

综上，预处理时间复杂度O(n^{\frac{1}{3}})，单组询问时间复杂度O(n^{\frac{1}{6}})。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e7+5;
const int mod=998244353;
#define ll long long
template <class T>
void read(T &x) {
	static char ch;static bool neg;
	for(ch=neg=0;ch<'0' || '9'<ch;neg|=ch=='-',ch=getchar());
	for(x=0;'0'<=ch && ch<='9';(x*=10)+=ch-'0',ch=getchar());
	x=neg?-x:x;
}
bool notprime[maxn];
int prime[maxn/14],cnt,phi[maxn],sum[maxn];
void init(){
	notprime[1]=phi[1]=1;
	for(int i=2;i<maxn;i++){
		if(!notprime[i]) prime[cnt++]=i,phi[i]=i-1;
		for(int j=0;j<cnt&&prime[j]*i<maxn;j++){
			notprime[i*prime[j]]=1;
			if(i%prime[j]==0){
				phi[i*prime[j]]=phi[i]*prime[j];break;
			}
			phi[i*prime[j]]=phi[i]*phi[prime[j]];
		}
	}
	for(int i=1;i<maxn;i++) sum[i]=(phi[i]*1ll*i%mod+sum[i-1])%mod,phi[i]=(phi[i]+phi[i-1])%mod;
}
int T,m,l,r,mid;
ll ans;
__int128 n,one=1,tmp;//one用来使某些运算过程中强制类型转换为int128 
int main(){
	init();
	scanf("%d",&T);
	while(T--){
		read(n);
		if(n<8){
			m=n;
			cout<<m<<"\n";
			continue;
		}
		l=1,r=maxn-5;
		while(l<=r){//就想用二分求n开三次方根 
			mid=(l+r)>>1;
			if(one*mid*mid*mid>n) r=mid-1;
			else l=mid+1,m=mid;
		}
		int k=sqrt(m+0.5);
		ans=0,tmp=one*m*m*m;
		for(int i=1;i<=k;i++){
			if(m%i==0){
				ans=(ans+(phi[i]-phi[i-1])*(n/i-(tmp-1)/i))%mod;
				if(m/i!=i){
					ans=(ans+(phi[m/i]-phi[m/i-1])*(n/(m/i)-(tmp-1)/(m/i)))%mod;
				}
			}
		}
		m=m-1;
		ans=(ans+m*1ll*(m+1)/2)%mod;
		for(int l=1,r,tt;l<=m;l=r+1){
			tt=m/l;
			r=m/tt;
			tmp=tt*one*(tt+1)*(2*tt+1)/2;
			ans=(ans+(sum[r]-sum[l-1])*tmp)%mod;
			tt=tt*1ll*(tt+1)/2%mod;
			ans=(ans+3ll*(phi[r]-phi[l-1])*tt)%mod;
		}
		if(ans<0) ans+=mod;
		cout<<ans<<"\n";
	}
	return 0;
}

1012 Sequence （补题 By wtw）

https://www.cnblogs.com/intwentieth/p/11262363.html

1013 Code （补题 By cys）

判断两个凸包是否相交，暴力判断每个点是否在另一类点形成的凸包里面即可。

总结：

前两场多校三个人都在不同地方打，沟通上会浪费一些时间，而且不容易到位。这场我有个比较大的问题是wtw说了1013的正确做法，让我试试，但我看不懂题，没有选择相信他，有点对不住队友。

最后，感觉我们似乎并没有足够的时间来掌握好各自承担的锅，时间比想象中更紧迫。。。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值