算法--查找

删除元素
第十一章 27

给定一个数组和一个值，在原地删除与值相同的数字，返回新数组的长度。元素的顺序可以改变，并且对新的数组不会有影响。
样例：
给出一个数组 [0,4,4,0,0,2,4,4]，和值 4
返回 4 并且 4 个元素的新数组为[0,0,0,2]

分析：
题目已经暗示可以将需要删除的元素移至数组末尾，因此用两个下标 m 和 n，m 用来从左至右遍历数组寻找该元素，n 从右至左记录可以用来交换的尾部位置。

// An highlighted block
def removeElement(A,elem):
    if None == A:
        return A
    len_A = len(A)
    m = 0
    n = len_A-1
    ###用两个下标 m 和 n，m 用来从左至右遍历
    # 数组寻找该元素，n 从右至左记录可以用来交换的尾部位置
    while m <=n:
        if elem==A[m]:
            if elem!=A[n]:
                A[m],A[n]=A[n],A[m]
                m+=1
                n-=1
            else:
                n-=1
        else:
            m+=1
    for i in range(n+1):
        A.pop()
    return A

if __name__ =='__main__':
    A=[0,4,4,0]
    elem = 0
    print(removeElement(A,elem))

----2020/3/11

----二分查找的时间复杂度（ ）
正确答案: C
O(N*log(N))
O(N)
O(log(N))
O(N^2)

解析：因为二分查找每次排除掉一半的不适合值，所以对于n个元素的情况：
一次二分剩下：n/2
两次二分剩下：n/2/2 = n/4
。。。
m次二分剩下：n/(2^m)
在最坏情况下是在排除到只剩下最后一个值之后得到结果，所以为
n/(2^m)=1;
2^m=n;
所以时间复杂度为：log2(n)

----对线性表进行折半查找时，要求线性表必须以链式方式存储，且结点按关键字有序排列，这样的说法正确吗？
正确答案: B
正确
不正确

解析：折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。
为什么采取顺序存储结构：折半查找需要先对查找的数据集合排序，并且每次要获得数据列表的中间位置，通过数组这种顺序存储结构，只要一次索引就能获得中间值，如果是链式结构，就每次都要从头遍历到中间位置，耗费大量时间。

----设有序表中有1000个元素，则用二分查找查找元素X最多需要比较（）次。

正确答案: B
25
10
7
1
解析：这里可以利用完全二叉树的思想，所有的节点个数为1000个，求树的最小高度的问题。当高度为10时，能查找到1023个元素。

----设一组初始记录关键字序列为(13，18，24，35，47，50，62，83，90，115，134),则利用二分法查找关键字90需要比较的关键字个数为（）。
正确答案: B
1
2
3
4
解析：13 ---- 134 -->50 第一次
62 ---- 134 -->90 第二次

----

----对于满足折半查找和分块查找条件的文件而言,无论它存在何种介质上,均能进行顺序查找,折半查找和分块查找()
正确答案: B
对
错

解析：存储在顺序介质如磁带上，无法随机读写。自然无法二分与分块。

----在长度为n的顺序线性表中顺序查找值为x的元素时，查找成功时的平均查找长度（假定查找每个元素的概率均相等）为（）。
正确答案: D
n
(n-1)/2
n/2
(n+1)/2
解析：长度为n的线性表顺序查找x，则查找次数可能是1,2,3,…,n次，则和sum为n*(1+n)/2，所以平均查找次数为sum/n=(n+1)/2

----具有12个关键字的有序表，折半查找的平均查找长度（）
正确答案: A
3.1
4
2.5
5

解析：将12个数画成完全二叉树，第一层有1个、第二次2个、第三层4个，第四层只有5个。
二分查找时：
第一层需要比较1次
第二两个数，每个比较2次
第三层四个数，每个比较3次
第四层五个数，每个比较4次
则平均查找长度即为：（1+22+34+4*5）/12 = 37/12 = 3.0833 即为 A、3.1

----设有序顺序表中有n个数据元素，则利用二分查找法查找数据元素X的最多比较次数不超过（）。

正确答案: A
log2n+1
log2n-1
log2n
log2(n+1)
解析：log2(n)+1

----二叉查找树的查找效率与二叉树的树型有关，在（）时其查找效率最低
正确答案: C
结点太多
完全二叉树
是单枝树
节点太复杂
解析：当二叉查询树变成一条链表效率最差。

----有个长度为12的无重复有序表，按折半查找法进行查找，在表内各元素等概率情况下，查找成功所需的平均比较（三元比较）的次数为（）
正确答案: B
35/12
37/12
39/12
43/12

解析：由题目已知元素序号(即下标)范围为1～12。查找1次成功的结点为：6。查找2次成功的结点为：3，9。查找3次成功的结点为：1，4，7，11。查找4次成功的结点为：2，5，8，10，12。成功查找所有结点的总的比较次数为:1×1+2×2+3×4+4×5=37平均比较次数为37／12。因此选择B

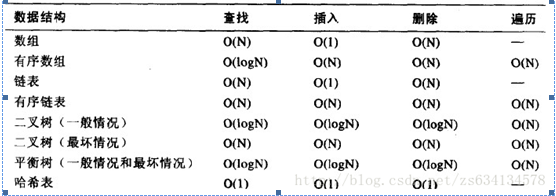
----对于关键字序列（16,10,20,12,18,7,14,13,5,19），不可能构成其二叉排序树中一条查找路径的序列是（ ）
正确答案: C
16,10,7,5
16,20,18,19
16,10,7,12,14
16,10,12,14

解析：。。。。。。

----折半查找与二元查找树的时间性能在最坏的情况下是相同的()
正确答案: B
对
错

解析：折半查找的查找长度至多为㏒2 n +1，二元查找树最坏时需查找n次(数列有序，树只有左孩子或只有右孩子，退化为线性表)

----假设在有序线性表A[1…30]上进行二分查找,则比较五次查找成功的结点数为（ ）
正确答案: C
8
12
15
16
解析：

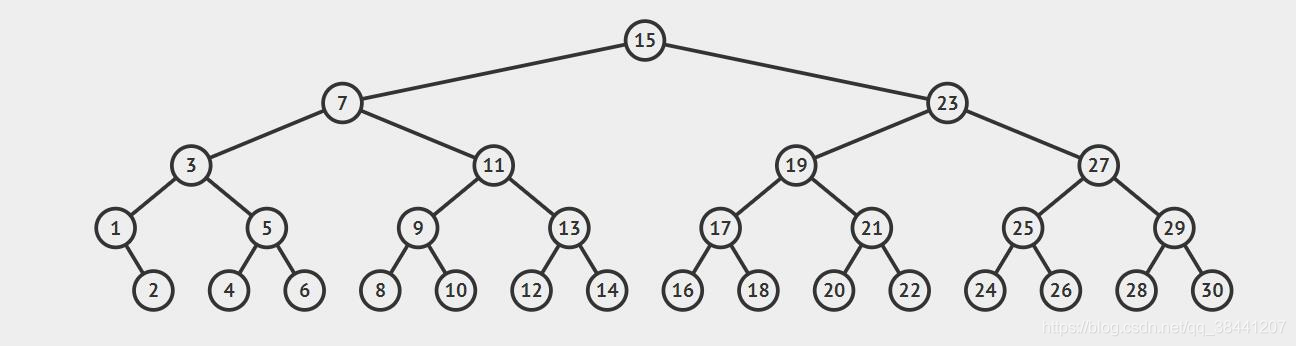
查找一次成功的节点数为1，值为15
查找二次成功的节点数为2，值为7,23
查找三次成功的节点数为4,值为3,11,19,27
查找四次成功的节点数为8，值为1,5,9,13,17,21,25,29
查找五次成功的节点数为15，值为2,4,6,8,10,12,14,16,18,20,22,24,26,28

----在154个元素组成有序表进行二分法查找，可能的比较次数为
正确答案: B C D
10
8
4
1
解析：[log2(154)] = 7，最差的情况下找8次，所以8次及8次以内都有可能找到。

----下面哪一方法可以判断出一个有向图是否有环(回路)()
正确答案: A B
深度优先遍历
拓扑排序
Dijkstra求最短路径
求关键路径

解析：22
绝对能判断有向图是否有环的是：
1.DFS
2.拓扑排序
3.最短路径是允许有环的！C肯定不选。
4.D可选可不选。

----2020/3/30

----用二分法查找长度为10的、排好序的线性表，查找不成功时，最多需要比较多少次？
正确答案: B
3
4
5
6
解析：二分查找，可以用二叉判定树，查找不成功的次数不超过判定树的深度，即（log2n）+1，其中log2n向下取整。

----对有序数组{2、11、15、19、30、32、61、72、88、90、96}进行二分查找，则成功找到15需比较（）次
正确答案: C
3
4
2
5
解析：C
0 1 2 3 4 5 6 7 8 9 10
2、11、15、19、30、32、61、72、88、90、96
第一次 index=（0+10）/2=5 对应32 ； 比15大 所以下次范围是 0到4
第二次 index=（0+4）/2=2 对应15 找到

----2020/3/31

----已知有序序列b c d e f g q r s t,则在二分查找关键字b的过程中，先后进行比较的关键字依次是多少?()
正确答案: B
f d b
f c b
g c b
g d b
解析：b c d e f g q r s t 二分查找，折半法
① low = 0,high = 9,mid = (low+ high)/2=4, ∴ 'b’比较a[4]=‘f’，＜,找左边 ( b~e )
② low = 0,high = mid-1 = 3, mid = 3/2=1, ∴ 'b’比较a[1]=‘c’ , ＜，找左边（b~d）
③ low = 0,high = mid -1 = 0,mid = 0,∴ ‘b’ 比较a[0] = ‘b’，找到（若未找到，low=high，也停止查找）
所以比较的顺序就是f c b

----在ASC算法team日常开发中，常常面临一些数据结构的抉择，令人纠结。目前大家在策划一个FBI项目（Fast Binary Indexing），其中用到的词汇有6200条，词汇长度在10-15之间，词汇字符是英文字母，区分大小写。请在下面几个数据结构中选择一个使检索速度最快的：
正确答案: D
二叉搜索树，比较函数开销：1次运算/每字符
哈希表，hash算法开销：10次运算/每字符
链表，比较函数开销：1次运算/每字符
TRIE树，寻找子节点开销：1次运算/每字符
解析：Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。
它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希表高。

----2020/4/2

----在有序表( 7, 13, 33, 87, 99, 97, 117, 123,129,131,137)中，使用二分查找算法查找13时需要的关键字比较次数是（）
正确答案: A
4
3
2
5
解析：left, right=0,10
step1. mid=(left+right)//2=5 num[5]=97 13<97 right=mid-1=4
step2. mid=(left+right)//2=2 num[2]=33 13<33 right=mid-1=1
step3. mid=(left+right)//2=0 num[0]=7 13>7 left=mid+1=1
step4. mid=(left+right)//2=1 num[1]=13 13==13 break

----广告系统为了做地理位置定向，将IPV4分割为627672个区间，并标识了地理位置信息，区间之间无重叠，用二分查找将IP地址映射到地理位置信息，请问在最坏的情况下，需要查找多少次?
正确答案: D
17
18
19
20
解析：即求树的深度为log2(627672 )+1

----判断下列说法是否正确：对长度为n的有序表进行折半查找的判定树的高度为「log2n（）
正确答案: B
正确
错误
解析：此题是考查数据结构二分查找问题。
其判定树的高度，也就是为最坏一次查找时，需要比较的次数，所以为[log2n+1]。

----2020/4/2

----若在线性表中采用折半查找法查找元素，该线性表应该：

正确答案: C
元素按值有序
采用顺序存储结构
. 元素按值有序且采用顺序存储结构
元素按值有序且采用链式存储结构
解析：首先折半查找，必须要求地址是连续的，数组，而且有明确的边界。然后还要求数组里面存放的数据是有序的，要不然无异于随机查找。

----众里寻他千百度，蓦然回首，那人却在灯火阑珊处。——辛弃疾《青玉案》描述的是()
正确答案: B
贪心
回溯
穷举
分治
递归
解析：回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

----若有一个顺序有序表A[1:18] 中有18个元素，现进行二分查找，则查找 A［3］的比较序列的下标依次为（ ）。

正确答案: D
1，2，3
9，5，2，3
9，5，3
9，4，2，3
解析：假设[1:18]是单调递增，设A[3] = x。
先查找[1:18]的中间值mid=（1+18）/2=9.5，向下取整为9,
A[9] > x，于是范围变成了中值左边的取值，左右值变成了[1:9-1]即为[1:8]
mid =（1+8）/2=4.5，取值4
A[4] > x，于是范围变成了中值左边的取值，左右值变成了[1:4-1]即为[1:3]
mid = (1+3)/2 = 2
A[2] < x，于是范围变成了中值右边的取值，范围变成[2+1:3]即为[3:3]
A[3] = X
由上：查找 A［3］的比较序列的下标依次为（9,4,2,3 ）。

----下列哪个查找最快?
正确答案: A
哈希表法（散列表）
顺序查找
二分查找
二叉排序树查找
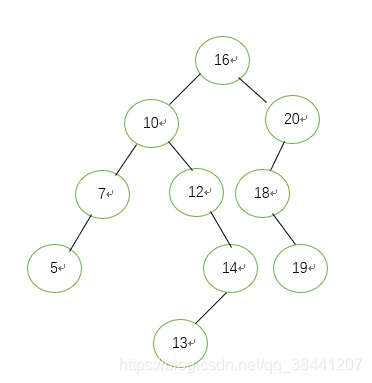
解析：无论是基于线性查找表、二叉树搜索树、还是多路搜索树，凡是基于关键字比较的方法，其时间复杂度范围都为：O(logn)~O(n)
由于哈希表原因，其查找时间复杂度为：O(1)

----下列说法中错误的是：（）
正确答案: C
插入排序某些情况下复杂度为O（n）
排序二叉树元素查找的复杂度可能为O（n）
对于有序列表的排序最快的是快速排序
在有序列表中通过二分查找的复杂度一定是O（log2n）
解析：A：数据有序时，插入排序的时间复杂度就是O(n)
B：比如只有右孩子结点的树
C：快排是在无序的情况下排序比较快，所以C说法不正确
D：一定是O(nlog2n)
对于有序的列表，排序最快的是插入排序，时间复杂度O(N)。

----下列选项中，不能构成折半查找中关键字比较序列的是 （）。

正确答案: A
500,200,450,180
500,450,200,180
180,500,200,450
180,200,500,450
解析：画出查找路径图，因为折半查找的判定树是一棵二叉排序树，看其是否满足二叉排序树的要求。