二叉树的相关知识

二叉树

概念

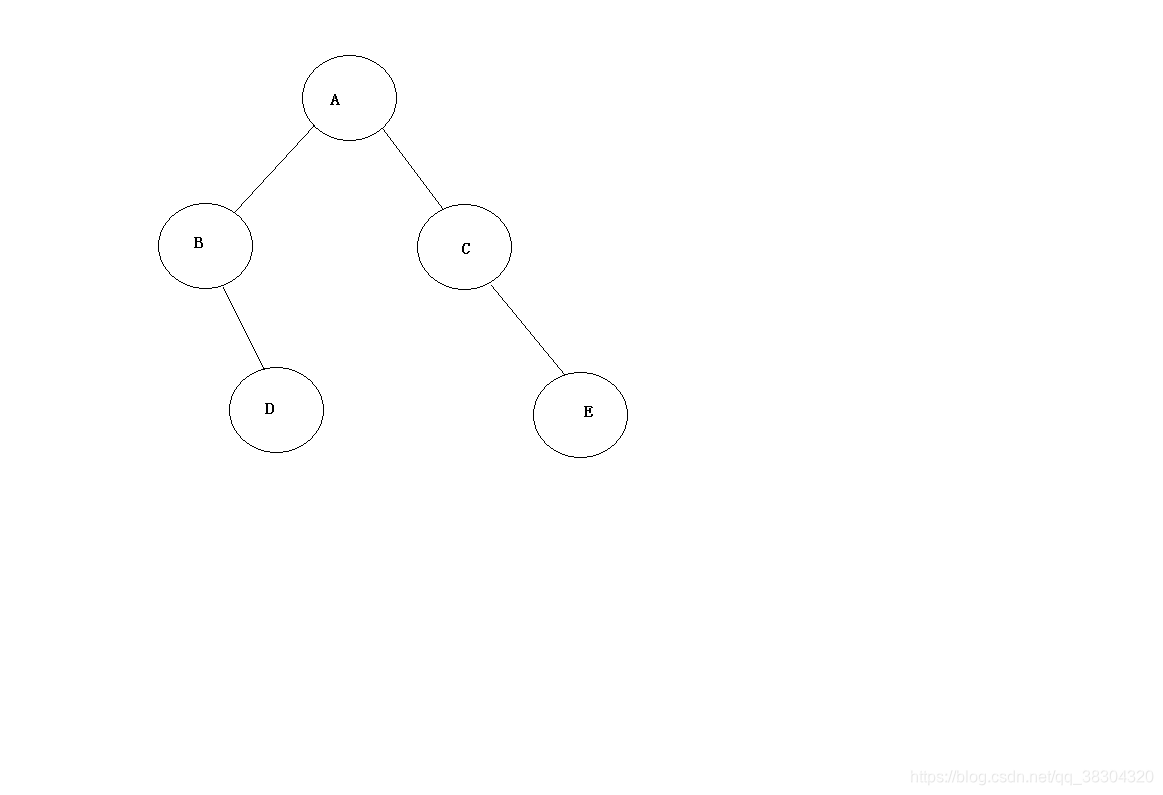
二叉树是n(n>=0)个节点的有限集合，该集合或者为空集（即空二叉树），或者有一个根节点和俩棵互不相交的，分别称为根节点的左右子树组成，

如图所示：

Note：
1.二叉树的每个结点的度<=2
2.左右子树是有顺序的，次序不能够颠倒。
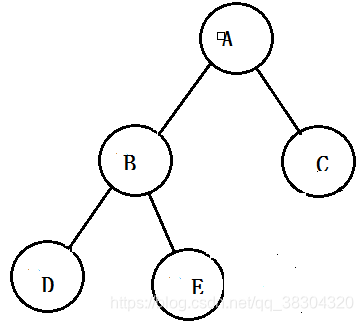
下面是俩棵不同的二叉树

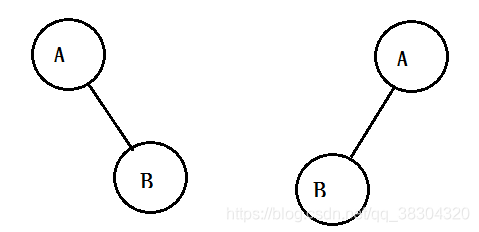
二叉树的性质：

1.在二叉树的第n层中，至多有2^(n-1)个结点（n>0）
2.深度为k的二叉树至多有2^K-1个结点（k>=1）
3.对于任何一个二叉树T ，如果其终端结点数(叶子节点)为n0，度为2的结点数为n2
则 n0 =n2+1
4.具有n个结点的完全二叉树的深度为

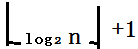
5.如果对一颗有n个结点的完全二叉树(其深度为以上图所示)的结点按层序编号，对于任一节点i(1<=i<=n)有一下性质：

如果i=1，则节点i是二叉树的跟，无双亲；如果i>1,则其双亲是节点|_ i/2 _|
如果2i>n，则节点i 无左孩子(节点i为叶子节点)； 否则其左孩子是结点2i
如果2i+1>n ,则结点i无右孩子，否则其右孩子是结点2i+1

特殊的二叉树：

满二叉树

在一棵二叉树中，如果所有的分支结点都存在左右子树，并且所有叶子结点都存在同一层，这样的数称之为满二叉树。
如图所示

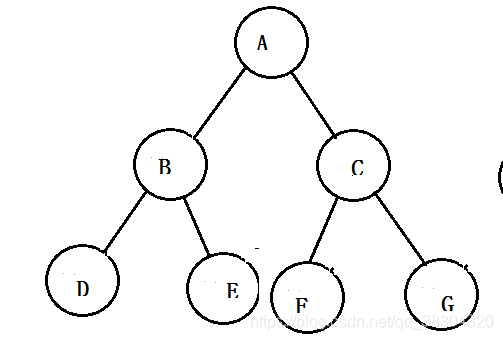
满二叉树的特点

叶子只能出现最下一层
非叶子节点的度一定是2
在同样深度的二叉树中，满二叉树的结点个数一定是最多，同时叶子结点也是最多

完全二叉树

对一颗具有n个节点的二叉树按层序进行编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同，则这颗二叉树称为完全二叉树

完全二叉树特点

叶子结点只能出现最下2层
最下层的叶子一定集中在左部连续位置
倒数第二层，如有叶子结点，一定都在右部连续位置
如果结点度为1，则该节点只有左孩子
同样的结点树的二叉树，完全二叉树的深度最小。

满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树

一道关于二叉树的例题：
如果一个完全二叉树的结点总数为349个，求叶子结点的个数。

由二叉树的性质知：n0=n2+1，将之带入349=n0+n1+n2中得：349=n1+2n2+1，因为完全二叉树度为1的结点个数要么为0，要么为0，那么就把n1=0或者1都代入公式中，很容易发现n1=1才符合条件。
。所以算出来n2=174，所以叶子结点个数n0=n2+1=175。

由此我们可以推断：

如果一棵完全二叉树的结点总数为n，那么叶子结点等于n/2（当n为偶数时）或者(n+1)/2（当n为奇数时）

二叉树的遍历

二叉树的遍历主要有3种方式，分别是前序遍历，中序遍历，以及后序遍历

前，中 ， 后，主要是针对根节点来说的。

主要是靠递归进行实现的

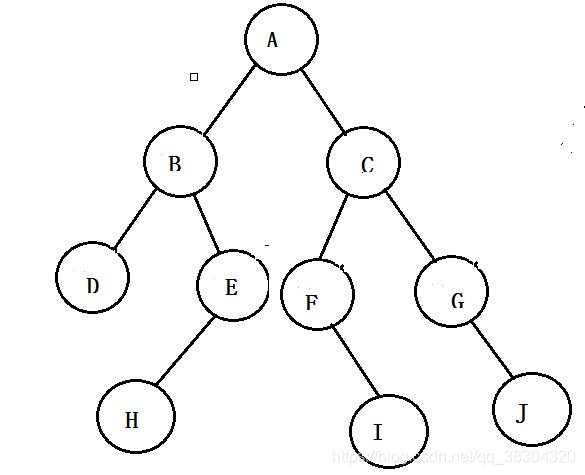
对于以上图：
前序遍历： A B D E H C F I G J
中序遍历 ： D B H E A F I C G J
后序遍历： D H E B I F J G C A