

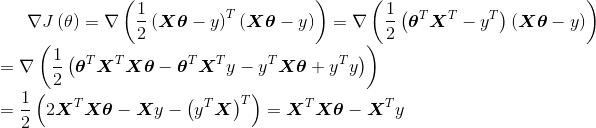

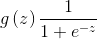





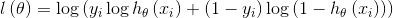


第一课:线性回归
假如银行是根据顾客的工资和年龄来预测贷款多少,这样工资和年龄就是特征,而贷款值就是标签,这就是一个回归问题:就是我们在预测时候,得到的结果是一个完整的值(这个值要求在一定区间内)。从数学层面上来讲,两个特征分别是两个坐标,而标签就是函数值,而线性回归就是寻找一条线来最好地拟合我们的数据点。



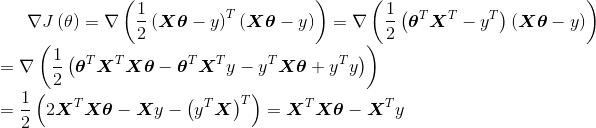

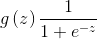





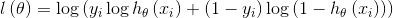


假如银行是根据顾客的工资和年龄来预测贷款多少,这样工资和年龄就是特征,而贷款值就是标签,这就是一个回归问题:就是我们在预测时候,得到的结果是一个完整的值(这个值要求在一定区间内)。从数学层面上来讲,两个特征分别是两个坐标,而标签就是函数值,而线性回归就是寻找一条线来最好地拟合我们的数据点。

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


