Davies-Bouldin指数（DBI）

Davies-Bouldin指数（DBI）（由大卫L·戴维斯和唐纳德·Bouldin提出）是一种评估度量的聚类算法。

以下是对这个算法的理解：

假如我们有一堆数据点，我们把它们分成n个簇类。公式们如下：

1、DBI定义了一个分散度的值Si：表示第i个类中，度量数据点的分散程度，

计算公式为：

 

Xj表示第i类中第j个数据点；Ai表示第i类的中心；Ti表示第i类中数据点的个数；q取1表示：各点到中心的距离的均值，q取2时表示：各点到中心距离的标准差，它们都可以用来衡量分散程度。

2、DBI定义了一个距离值Mij：表示第i类与第j类的距离，

计算公式为：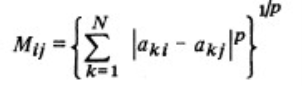

aki 表示第i类的中心点的第K个属性的值，Mij则就是第i类与第j类中心的距离。

3、DBI定义了一个相似度的值Rij：

计算公式为： 衡量第i类与第j类的相似度。

4、通过以上公式的计算，我们再从Rij中选出最大值Ri=max（Rij），即，第i类与其他类的相似度中最大的相似度的值。

最后计算每个类的这些最大相似度的均值，便得到了DBI指数：，

分类个数的不同可以导致不同的值，值越小，分类效果越好。

图例：

                 

    左图表示不同簇类数目下数据点的分类情况，右图表示在不同的簇类数目下，R值的变化。

 

    总的来说，这个DBI就是计算类内距离之和与类间距离之比，来优化k值的选择，避免K-means算法中由于只计算目标函数Wn而导致局部最优的情况。