DCGAN深度卷积生成对抗网络

1、什么是GAN

GAN 主要包括了两个部分

• 生成器 generator
  生成器主要用来学习真实图像分布从而让自身生成的图像更加真实，以骗过判别器。
• 判别器 discriminator。
  判别器则需要对接收的图片进行真假判别。
• 过程：生成器努力地让生成的图像更加真实，而判别器则努力地去识别出图像的真假，这个过程相当于一个二人博弈，随着时间的推移，生成器和判别器在不断地进行对抗，最终两个网络达到了一个动态均衡：生成器生成的图像接近于真实图像分布，而判别器识别不出真假图像，对于给定图像的预测为真的概率基本接近 0.5（相当于随机猜测类别）。

对于 GAN 更加直观的理解可以用一个例子来说明：造假币的团伙相当于生成器，他们想通过伪造金钱来骗过银行，使得假币能够正常交易，而银行相当于判别器，需要判断进来的钱是真钱还是假币。因此假币团伙的目的是要造出银行识别不出的假币而骗过银行，银行则是要想办法准确地识别出假币。

因此，我们可以将上面的内容进行一个总结。给定真 = 1，假 = 0，那么有：
对于给定的真实图片（real image），判别器要为其打上标签 1；
对于给定的生成图片（fake image），判别器要为其打上标签 0；
对于生成器传给辨别器的生成图片，生成器希望辨别器打上标签 1。

2、GAN的训练过程

上面大家应该已经对GAN有了一个基本的认识，那么GAN是如何来做的呢？
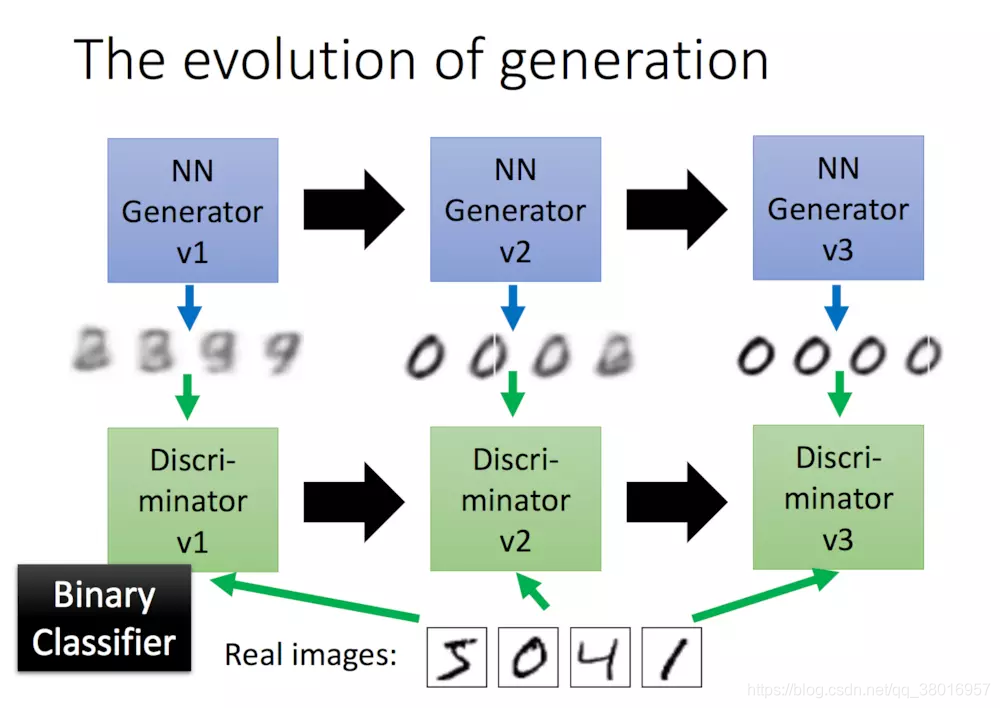
（1）首先，我们有一个第一代的Generator（一个神经网络，可产生概率值，也可回归而产生多个值，构成一张图片），然后他产生一些图片，然后我们把这些生成图片（负样本）和一些真实的图片（正样本）丢到第一代的Discriminator里面去学习，让第一代的Discriminator（二分类模型）能够的分辨生成的图片和真实的图片

（2）第一代Generator的进化：固定第一代训练好的Discriminator的参数值，重新训练让第一代的Generator，，直到第一代的Discriminator识别不出生成的图片。 即我们训练了第二代的Generator，第二代的Generator产生的图片，能够骗过第一代的Discriminator，
第一代Discriminator的进化：固定第二代Generator的参数值，让其生成图片，然后训练第一代的Discriminator，能够分辨出Generator产生的图片和真实图片。此时，我们完成了第二代的Discriminator训练，依次类推。

3、GAN数学原理

从最大似然讲起，给定数据分布Pdata(x)，同时有一个θ控制的分布（比如GMM：高斯分布混合模型，即一个数据分布服从多个高斯分布的权值相加）Pg(x;θ)，如何找到最好的θ，使得产生的数据分布和原始的分布最接近？

方法：
likelihood：使拟合的分布Pg也能以最大的概率值产出从数据分布Pdata采样的m个点
（1）从Pdata中采样x1,x2,…xm
（2）计算Pg(xi;θ)，使其最大

极大似然估计的化简过程：

• 1、先通过log将相乘转为相加
• 2、这里Pg为概率值，当我们取很多个点的时候，每个点的权重为1，因为这堆sample都是从Pdata(x)里面出来的，即可进行约等转换
• 3、概率*值=期望，在连续分布的情况下用积分即可。
• 4、转化为KL散度又称相对熵。设P(x)和Q(x)是X取值的两个概率概率分布，则对的相对熵为:
  
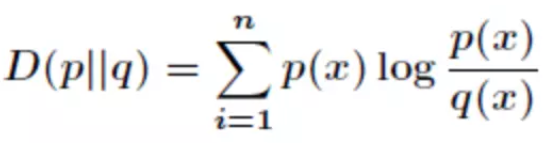
  在一定程度上，熵可以度量两个随机变量的距离。KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。
  
  我们需要一个很强大的数据生成器，也行GMM不够强，换成神经网络试试：
  每一个图片x都是通过神经网络的输入z映射生成的，我们希望产出的图片分布与真实图片的分布一样，
  而通过我们前面的likelihood推导：
  
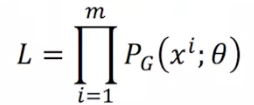
  需要求出生成的每一张图片的概率Pg(xi)，再最大化。
  而每一张图片Pg(xi)，都可以通过很多不同的输入z映射生成，所以要把能够生成这张图片的 所有输入的 z的概率做积分：
  *I():能够生成x为1，不能生成x则为0
  
  
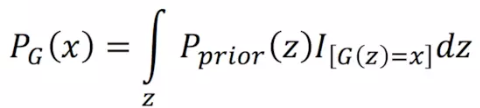
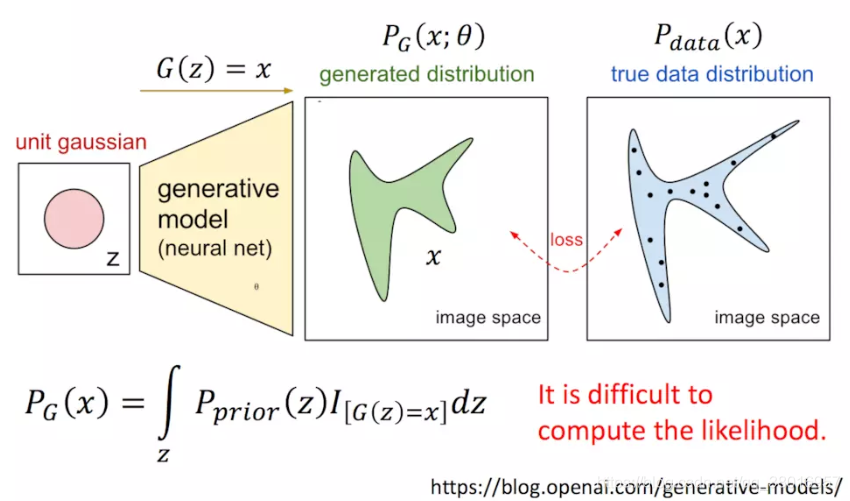
  而先验概率Pprior(z)是很难穷举的，所以很难求出Pg(x)。

接下来进入正题：
GAN要求解的最终目标：

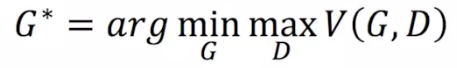
公式解释:假设G为离散的（其实是连续的，离散比较好解释），然后在每个G函数（蓝色曲线）中，找到最大的D参数，再在所有的D中，取最小的D值。

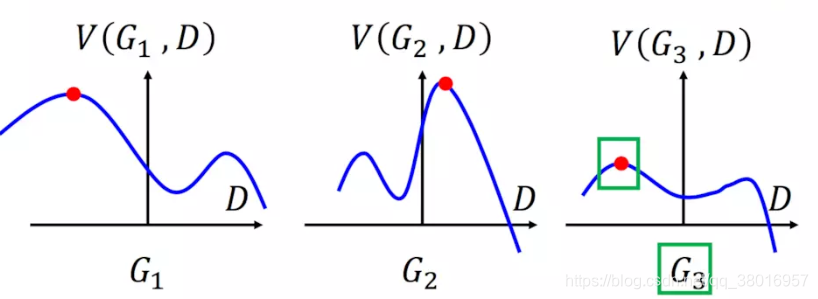
那么 ，V是什么，V写作下面的式子：
在真实世界中抽取x，再对logD(x)求期望，在生成器中抽取x，再对log(1-D(x))求期望

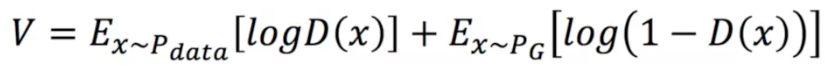
当我们的V写成下面这样子的时候，我们取maxV(G,D)就能表示Pg和Pdata的差异。
这里，对于一个给定的G，我们来求解maxV(G,D)：

• 首先期望=概率*值，对其积分
• 同对dx积分，相加
• 因为概率P在数据分布中是给定的，要找出max，即找出D(x)的最大值
  
  在函数f中，以D为参数，求导取最大值：
  
  
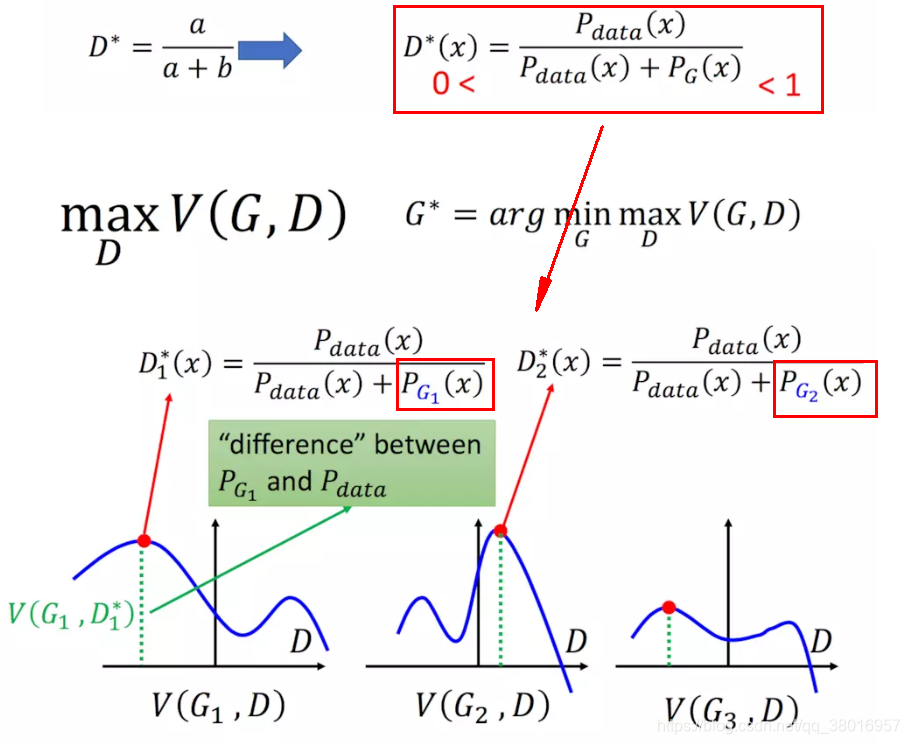
  找到了D的最大值之后，带回原式V，即可求得V的最大值
• 1-D(x)变换成Pg为分母
• 分子分母同时除以2，变成1/2乘以D(x)，且log相乘可以变成相加，所以可以提出1/2，留下分子中的2，方便凑成JS等式。
  
  JS散度：衡量两个分布之间的差异度
  所以，现在我们就明白了，按照上面的V的定义，我们就能得到二者的差距，当然我们可以定别的，就能产生别的散度度量。
  

从数学角度上来看GAN：

• 1、max：通过一个区分器D，算出JS散度和常数部分，能够最好的评估两个分布的差异度
• 2、min：通过一个生成器G，使区分器评估出来的差异度最小化
  
  那么，给定了一个G，我们能够通过最大化V函数得到D，那么我们如何求解G呢，用梯度下降就好了：
  *存在max，曲线并不是光滑的，为多个不同斜率的线段组合而成
  

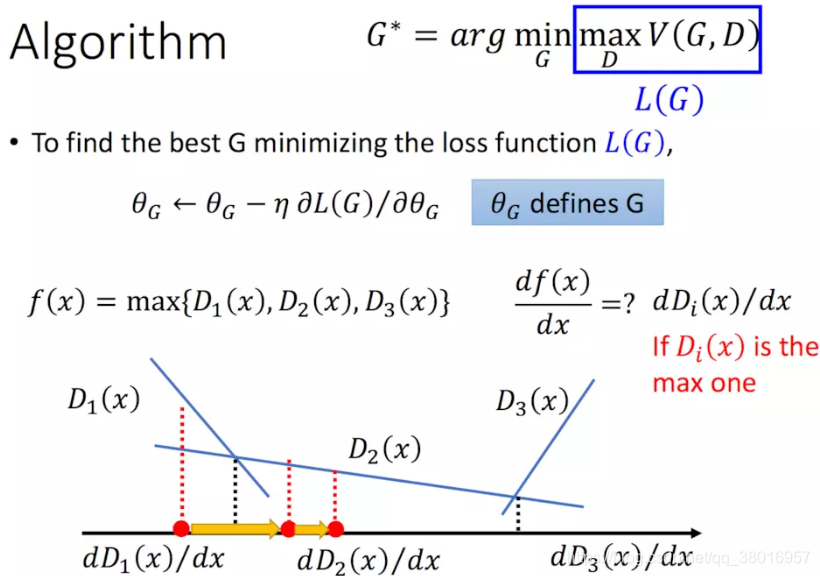
4、实际中的GAN

刚才我们讲的是理论部分的内容，V函数中存在积分，但是在实际中，Pdata和Pg我们是不知道的，我们没办法穷举所有的x，所以，我们只能采用采样的方法拟合积分，同时可以采用我们二分类的思路，我们把Pdata(x)中产生的样本当作正例，把Pg(x)产生的样本当作负例，那么，下面V可以看作是我们二分类的一个损失函数的相反数(少了负号）：

也就是说，最大化V的话，其实就是最小化我们二分类的损失，下面的Minimize少了一个负号，所以我们要找的D，就是能使二分类的损失最小的D，也就是能够正确分辨Pdata和Pg(x)的D，这也正符合我们想要找的discriminator的定义。

训练技巧：

在实际中，我们有可能做下面的变换，可以加快我们的训练速度：

• 变换前为红线，一开始训练时，斜率很小，训练很慢，

• 变换后，单调性一直，一开始斜率较大，训练较快