KMP

最新推荐文章于 2025-07-04 12:29:19 发布

沙发斯蒂芬大大

最新推荐文章于 2025-07-04 12:29:19 发布

阅读量361

点赞数 1

CC 4.0 BY-SA版权

分类专栏：算法

本文链接：https://blog.youkuaiyun.com/qq_38003454/article/details/108294683

本文详细介绍了KMP算法计算next值和nextVal值的过程，包括maxL的计算、next数组的获取，以及KMP算法的实现，特别强调了从0开始计算的推荐做法，并探讨了在文本串中查找模式串的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

KMP算法计算next值和nextVal值

KMP算法计算next值和nextVal值

给定一个主串S及一个模式串P，判断模式串是否为主串的子串；若是，返回匹配的第一个元素的位置（序号从1开始），否则返回0；

这里先不写算法，仅仅计算next和nextVal值

那么计算时只用到子串，也就是模式串

这里模式串为：abaabcac

第一步将模式串写上序号，我们这里从1开始（有的从0开始,写代码推荐从 0开始，少一些操作）

maxL

列出从第一个开始的子串，找出相等的前缀和后缀的个数

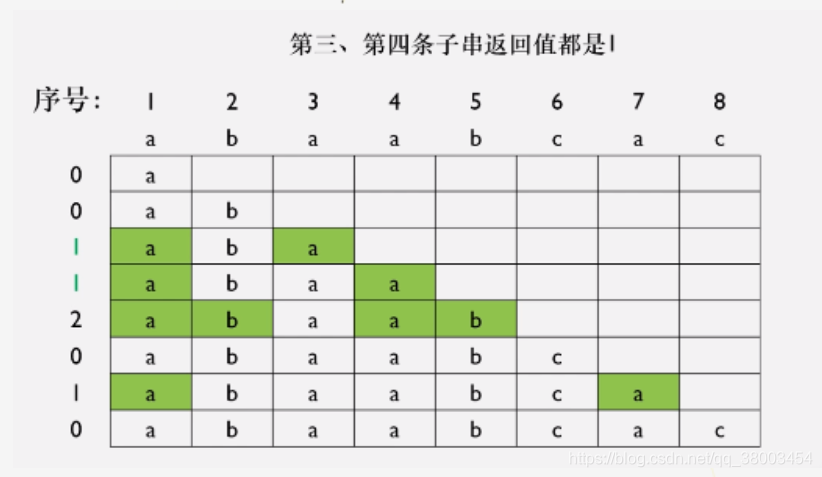
maxL 计算过程

maxL[i] = k 表示，以 i位置结尾的最长前后缀长度。

一般来说 : j 是前缀的结尾， i 是后缀的结尾。

前缀 = = 后缀，且前缀长度要小于（严格小于 1~i-1）

注意：以下图中 next 应为 maxL

0.初始化

下标从 1 开始， maxL[1] = 0; j = 1, i = 2;

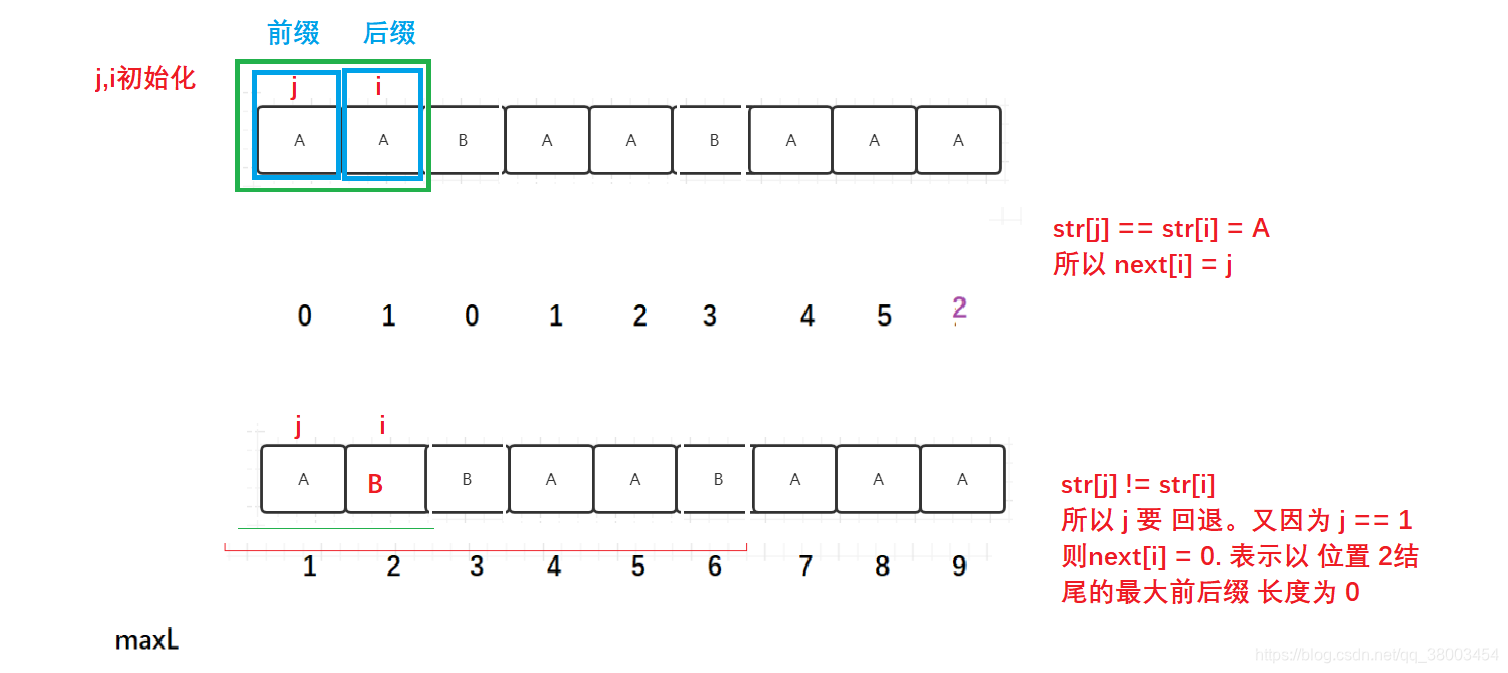
1.str[i] == str[j]

若 str[i] == str[j] , 则maxL[i] = j; j++; i++ ;

maxL[i] = j 的解释：由于maxL保存的以i位置结尾的最长前后缀长度。当str[i] == str[j] 时。

i 指向后缀的最后一个， j 指向前缀的的最后一个。由于下标从 1 开始。

所以 j 就是前缀的长度。恰好应该赋值给maxL[i]

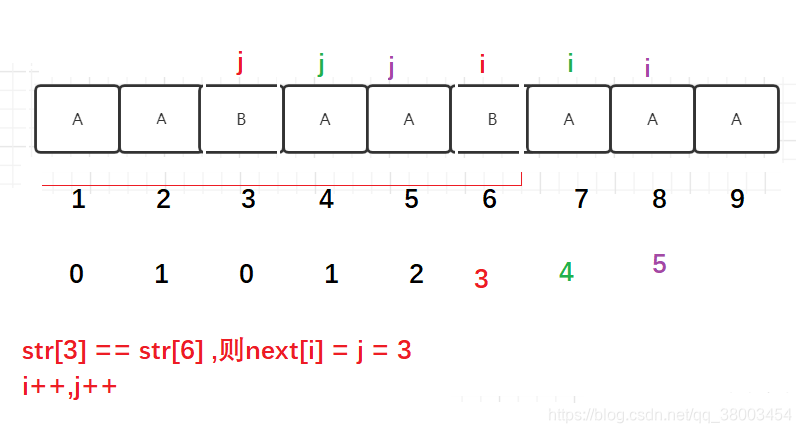
2.str[i] ！= str[j]

1. j 可以回退(j > 1)

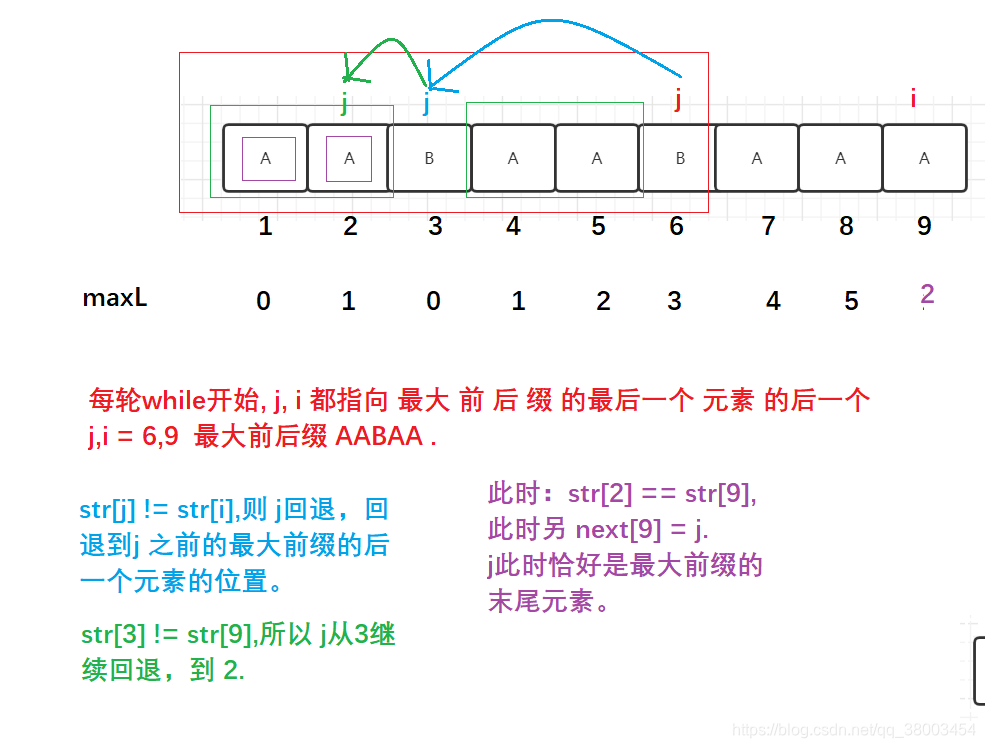
2.j == 1, j 不能回退。则 maxL[i] = 0, 必然为 0.

解释：当 str[i] == str[j] 时， j.i是增长的最大前后缀的末尾元素。

但是当 str[i] ！= str[j] 时， j,i 分别是最大前后缀的末尾元素的再后一个元素。

由于此时 j == 1 .j之前必然没有前缀了。所以maxL[i] = 0; 表示没有以 i 结尾的后缀。

代码

public  void getmaxL(String subStr, int[] maxL){
        // 下标从 1开始。
        subStr = " "+subStr; // 第 0 位 为 ' '  空格
        int j = 1, i = 2;
        maxL[1] = 0;
        while(i < maxL.length){
            // 每轮开始， i ,j 一定指向最大前后缀最后一个元素的 后 一个
            if(subStr.charAt(j) == subStr.charAt(i)){
                maxL[i] = j;  //  j == maxL[i-1] + 1; 当 连续递增时。
                i