Java基础之数据结构

本文中部分知识引自
http://www.ityouknow.com/java/2019/03/25/java-knowledge.html
https://www.cnblogs.com/ysocean/tag/Java数据结构和算法/
言归正传
数据结构是计算机存储，组织数据的方式，指相互之间存在一种或多种特定关系的数据元素的集合。
通常情况下，精心选择的数据结构可以带来更高的运行或存储效率，数据结构往往同高效的检索算法和索引技术有关。
（来源于百度百科）

常见的数据结构包括：

1》数组（Array）：在Java中，数组是用来存放同一种数据类型的集合，注意只能存放同一种数据类型(Object类型数组除外)

• 数组的声明
  ① 数据类型 [] 数组名称 = new 数据类型[数组长度]
  ② 数据类型 [] 数组名称 = {数组元素1，数组元素2，…}
• 访问数组元素以及给数组元素赋值
• 数组遍历

数组 插入快，查找慢，删除慢，大小固定，只能存储单一元素
有序数组比无序数组查询快，插入慢（需在指定的位置插入），删除慢，大小固定，只能存储单一元素

2》栈（stack）：限制插入和删除只能在一个位置上进行的线性表，该位置是表的末端，叫做栈顶（top）

• 栈的操作
  > 插入：进栈、入栈、压栈（也称push）
  > 删除：出栈、弹栈（也称pop）

• 结构类型
  > 顺序存储结构
  > 链式存储结构

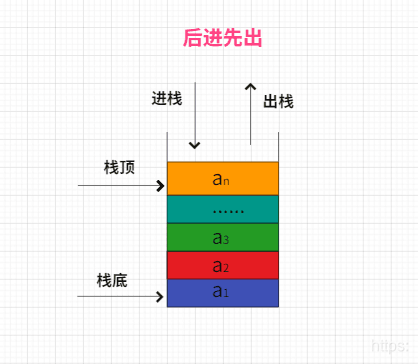
栈提供后进先出的存取方式 存取其他项很慢

应用场景：递归 —— 直接/间接 调用自身的函数

3》队列（queue）：一种受限制的线性表，它只允许在表的前端进行删除操作，在表的后端进行插入操作。进行插入操作的端称为队尾，进行删除操作的端称为队头

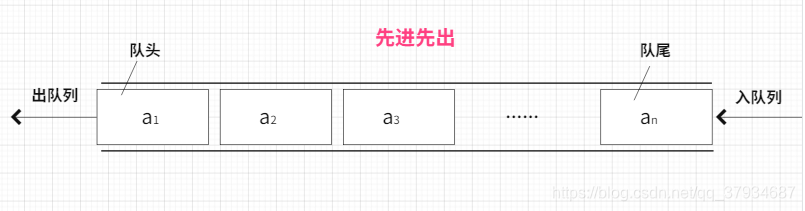
队列提供先进先出(FIFO)的存取方式 存取其他项很慢

应用场景：Mybatis里面的FifoCache

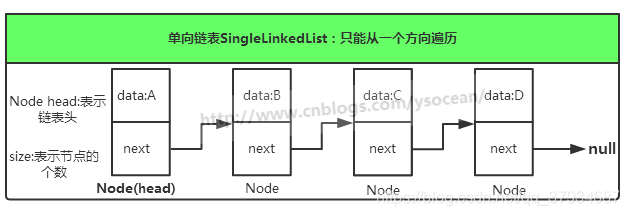
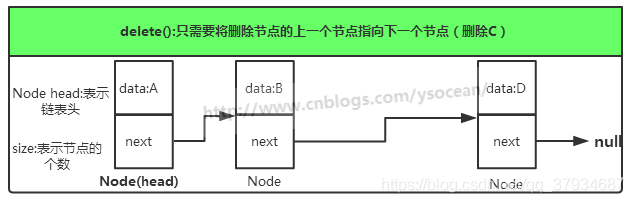
4》链表（Link）：由一连串节点组成，每个节点包含任意的实例数据（data fields）和一或两个用来指向上一个/或下一个节点的位置的链接
是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)

• 单向链表：一个单链表的节点（Node）分为两个部分，第一个部分（data）保存或者显示节点的信息，另一部分存储下一个节点的地址，最后一个节点的存储地址的部分指向空值
  单向链表只可向一个方向遍历，查找一个节点的时候需要从第一个节点开始访问下一个节点，一直访问到需要的位置
  
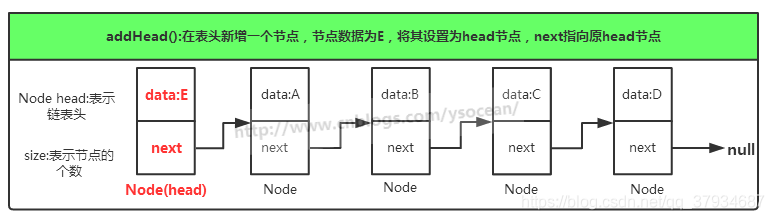
  插入一个节点的时候，只需要在链表头插入，将当前的节点设置为头节点，next指向原节点
  
  删除一个节点，将该节点的上一个节点的next指向该节点的下一个节点
  
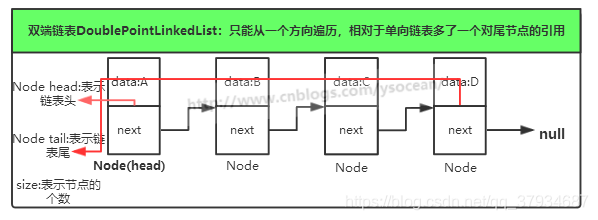
  双端链表：相对于单向链表多了一个队尾节点的引用
  
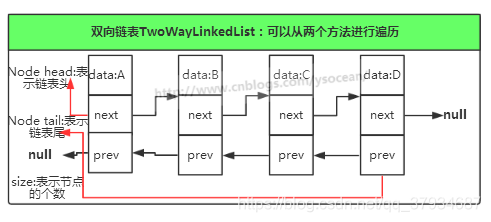
• 双向链表：一个双向链表的节点（Node）分为两个部分，第一个部分（data）保存或者显示节点的信息，另一部分存储对上一个节点的引用prev和下一个节点的引用next，最后一个节点的存储地址的部分指向空值
• 可以从两个方向进行遍历
  

链表插入和删除快 查找慢

以上链表的实现具体参考引用的链接 https://www.cnblogs.com/ysocean/p/7928988.html

5》哈希表（Hash Table）：也称散列表，是一种查找算法

• 根据关键字值（key - value）直接进行访问的数据结构
• 基于数组，通过把关键字映射到数组的某个下标来加快查找速度
• 把关键字转换为数组的下标，这个转换的函数称为哈希函数（也称散列函数），转换的过程称为哈希化

用的构造散列函数的方法：
（1）直接定址法： 取关键字或关键字的某个线性函数值为散列地址，即：h(key) = key 或 h(key) = a * key + b，其中 a 和 b 为常数
（2）数字分析法
（3）平方取值法： 取关键字平方后的中间几位为散列地址
（4）折叠法：将关键字分割成位数相同的几部分，然后取这几部分的叠加和作为散列地址
（5）除留余数法：取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址，即：h(key) = key MOD p p ≤ m
（6）随机数法：选择一个随机函数，取关键字的随机函数值为它的散列地址，即：h(key) = random(key)

哈希表，如果关键字已知则存取极快，删除慢；如果不知道关键字则存取慢，对存储空间使用不充分

6》堆（Heap）：是计算机科学中一类特殊的数据结构的统称，堆通常是一个可以被看做一棵树的数组对象

• 堆是非线性数据结构，它通常用数组来实现，相当于一维数组
  

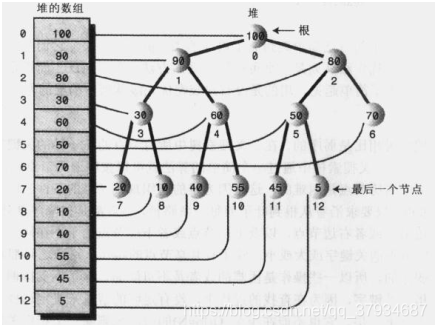
这种用数组实现的二叉树，假设节点的索引值为index，那么：
　节点的左子节点是 2index+1
　节点的右子节点是 2index+2
　节点的父节点是 （index-1）/2

• 堆中的每一个节点的关键字都大于（或等于）这个节点的子节点的关键字
• 它是完全二叉树，除了树的最后一层节点不需要是满的，其它的每一层从左到右都是满的。注意下面两种情况，第二种最后一层从左到右中间有断隔，那么也是不完全二叉树
  

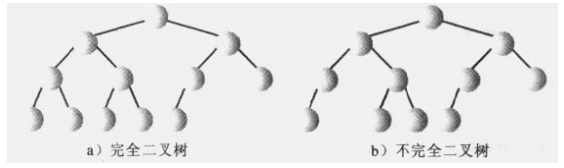
堆插入、删除快，队最大的数据存取快，对其他数据项存取慢
插入时：选择向上筛选，节点初始化时插入到数组最后一个空着的单元，数组容量大小增一。向上筛选只用和一个父节点进行比较，比父节点小就停止筛选
删除时：选择向下筛选，移走根，把最后一个节点移动到根的位置，一直向下筛选这个节点，直到它在一个大于它的节点之下，小于它的节点之上为止。向下筛选，将目标节点和其子节点比较，谁大就和谁交换位置

树（Tree）：是一种抽象数据类型（ADT），用来模拟具有树状结构性质的数据集合
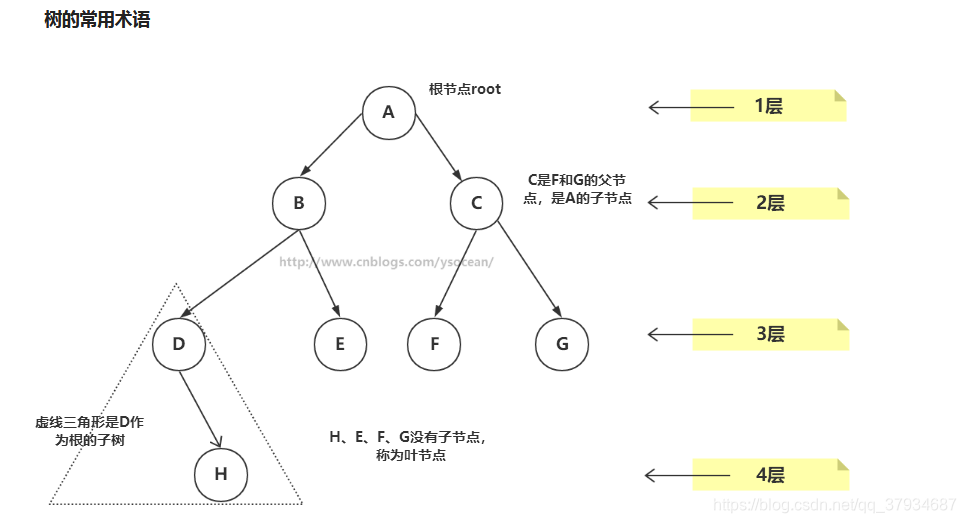上图为 " 多路树 "

①路径：顺着节点的边从一个节点走到另一个节点，所经过的节点的顺序排列就称为“路径”
②根：树顶端的节点称为根。一棵树只有一个根，如果要把一个节点和边的集合称为树，那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点
③父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；B是D的父节点
④子节点：一个节点含有的子树的根节点称为该节点的子节点；D是B的子节点
⑤兄弟节点：具有相同父节点的节点互称为兄弟节点；比如上图的D和E就互称为兄弟节点
⑥叶节点：没有子节点的节点称为叶节点，也叫叶子节点，比如上图的H、E、F、G都是叶子节点
⑦子树：每个节点都可以作为子树的根，它和它所有的子节点、子节点的子节点等都包含在子树中
⑧节点的层次：从根开始定义，根为第一层，根的子节点为第二层，以此类推
⑨深度：对于任意节点n,n的深度为从根到n的唯一路径长，根的深度为0
⑩高度：对于任意节点n,n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0

7》二叉树：树的每个节点最多只能有两个子节点
二叉搜索树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树

其查找、插入、删除的时间复杂度都为logN

• 查找节点：从根节点开始遍历，查找值等于当前节点值，则停止搜索（终止条件）；查找值小于当前节点值，则搜索左子树；查找值比当前节点值大，则搜索右子树；
• 插入节点：从根节点开始找要插入的位置（即新节点的父节点），新节点与当前节点比较，相同则表示已经存在且不能重复插入；若小于当前节点，则与根节点左子树比较，反之则与右子树比较，直到左子树为空或右子树为空，则插入到相应为空的位置
• 删除节点：主要分三种情况
  > 要删除的节点是叶节点（没有子节点） —— 改变该节点的父节点引用该节点的值，即将其引用改为 null
  > 要删除的节点有一个子节点 ——————— 将其父节点原本指向该节点的引用，改为指向该节点的子节点
  > 要删除的节点有两个子节点——————— 找到该节点的替换节点（后继节点：比删除节点大的最小节点）,替换要删
  除的节点为替换节点，然后删除替换节点

程序找到删除节点的右节点，(注意这里前提是删除节点存在左右两个子节点，如果不存在则是删除情况的前面两种)，然后转到该右节点的左子节点，依次顺着左子节点找下去，最后一个左子节点即是后继节点；如果该右节点没有左子节点，那么该右节点便是后继节点

8》红黑树：R-B Tree，全称是 Red-Black Tree，又称为“红黑树”，它一种特殊的二叉查找树。红黑树的每
个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)

• 每个节点或者是黑色，或者是红色
• 根节点是黑色
• 每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL 或NULL)的叶子节点！]
• 如果一个节点是红色的，则它的子节点必须是黑色的（反之不一定，即从每个叶子到根的所有路径上不能有两个连续的红色节点）
• 插入和删除的过程中，要遵循保持这些颜色的不同排列规则，即红-黑规则
• 从根节点到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点（即相同的黑色高度）
• 新插入的节点颜色总是红色的

红-黑树 的自我修正：

• 改变节点颜色
• 左旋
  
  
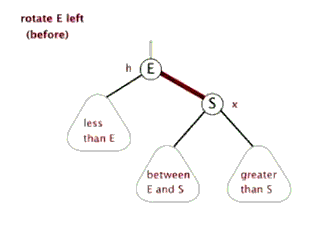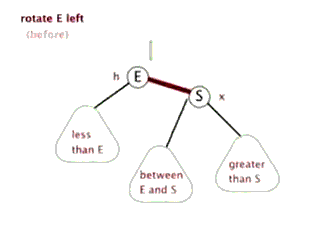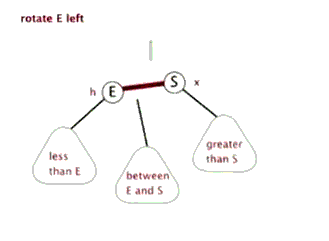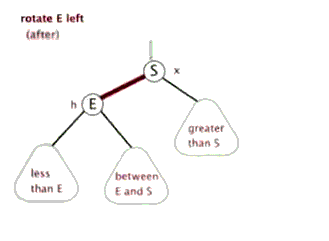
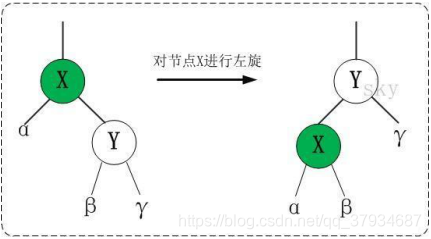
• 右旋
  
  
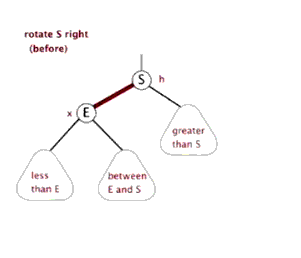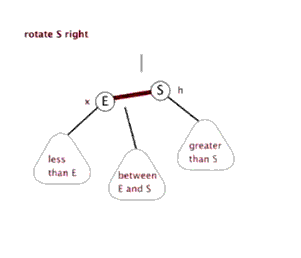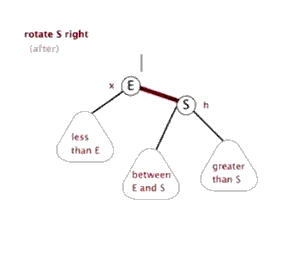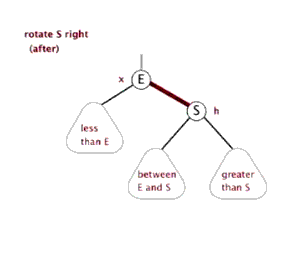
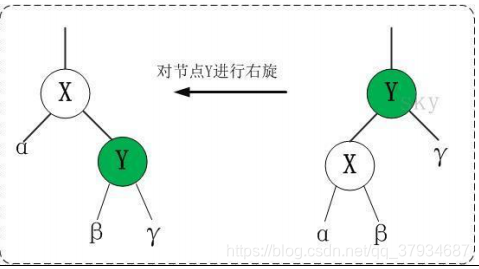
  插入操作：
• 将红黑树当作一颗二叉查找树，将节点插入
• 将插入的节点着色为"红色"
• 插入的节点是根节点，直接把此节点涂为黑色
• 插入的节点的父节点是黑色，什么也不需要做。节点被插入后，仍然是红黑树
• 遇到如下三种情况，我们就要开始变色和旋转（N：插入的节点 P：N的父节点 U：N的叔叔节点 G：N的祖父节点）
  ① 插入节点的父节点和其叔叔节点（祖父节点的另一个子节点）均为红色
  
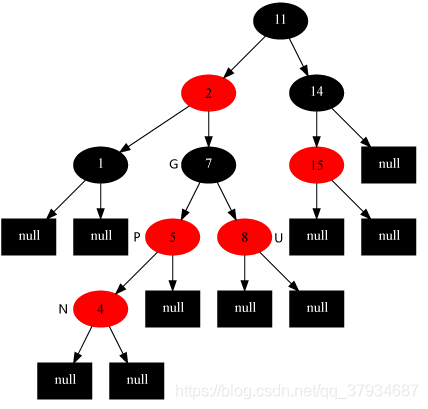
  处理方法：将当前节点(4) 的父节点(5) 和叔叔节点(8) 涂黑，将祖父节点(7)涂红,变成了下图所示的情况。再将当前节点指向其祖父节点，再次从新的当前节点开始算，这样就变成情况2了

② 插入节点的父节点是红色的，叔叔节点是黑色的，且插入节点是其父节点的右子节点(如下图)

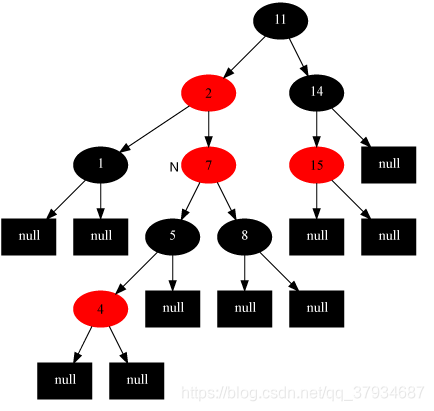
处理方法：将当前节点(7)的父节点(2)作为新的节点，以新的当前节点为支点做左旋操作，完成后如下图所示，这样就变成情况3了

③ 插入节点的父节点是红色的，叔叔节点是黑色的，且插入节点是其父节点的左子节点

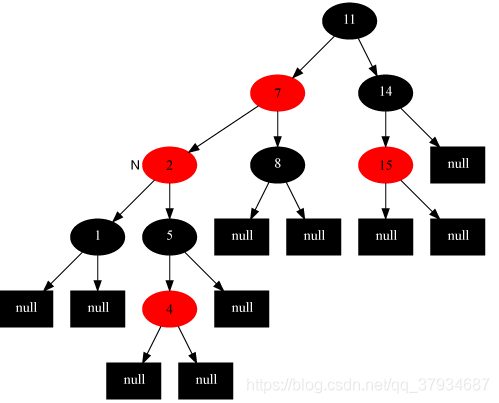
处理方法：将当前节点的父节点(7)涂黑，将祖父节点(11)涂红，在祖父节点为支点做右旋操作。最后把根节点涂黑，整个红-黑树重新恢复了平衡

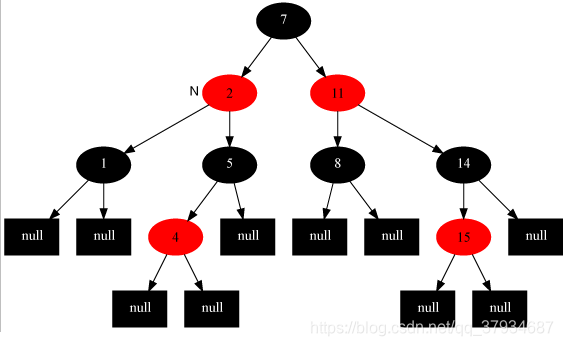
变色和旋转之间的先后关系可以表示为：变色->左旋->右旋

删除操作：

• 将红黑树当作一颗二叉查找树，将节点删除
• 同二叉查找树删除的方法是一样的
• 通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树

9》2-3-4树：参考 https://www.cnblogs.com/ysocean/p/8032648.html
10》图：参考 https://www.cnblogs.com/ysocean/p/8032659.html