穷举、贪心算法--泊松分酒（2）

泊松分酒问题：

初始酒量是 12 0 0，然后通过三个不同容量的瓶子（12L、8L、5L）倒出6L的酒出来

程序逻辑分析：

一下倒酒方式结果必须是可以结算出来的

当2为空的时候，1开始往2里面倒酒，出现两种情况，

一种：2满了，1还有剩余（2刚好满,1为0也考虑进来），这样的话就会出现1和2都有酒

另外一种：2没满，1没有剩余，这样的话1没有酒，2有酒

接上面，当2不为空，且3里面没满，出现两种情况

一种：3满了，2还有剩余（3刚好满2刚好为0也考虑进来），这样的话就会出现3和2都有酒

另外一种：3没满，2没有剩余，这样的话3有酒，2没有酒

接上面，当3满了之后，就向1里面添加酒，出现两种情况

一种：1满了，3还有剩余（1刚好满，3刚好为0也考虑进来），这样的话就会出现1和3都有酒

另外一种：1没满，3没有剩余，这的话就会出现1有酒，3没有酒的情况。

程序中参数解释：

b1 ，b2，b3指的是瓶子的容量；

bb1，bb2，bb3指的是瓶子内的酒量；

代码：

解释：有人会有疑问bb3==m是多余的，因为当前bb3的取值范围是bb3<=b3，这就是它的取值范围。但是b3的初始化值是会发送改变的，因为程序是会被改的。

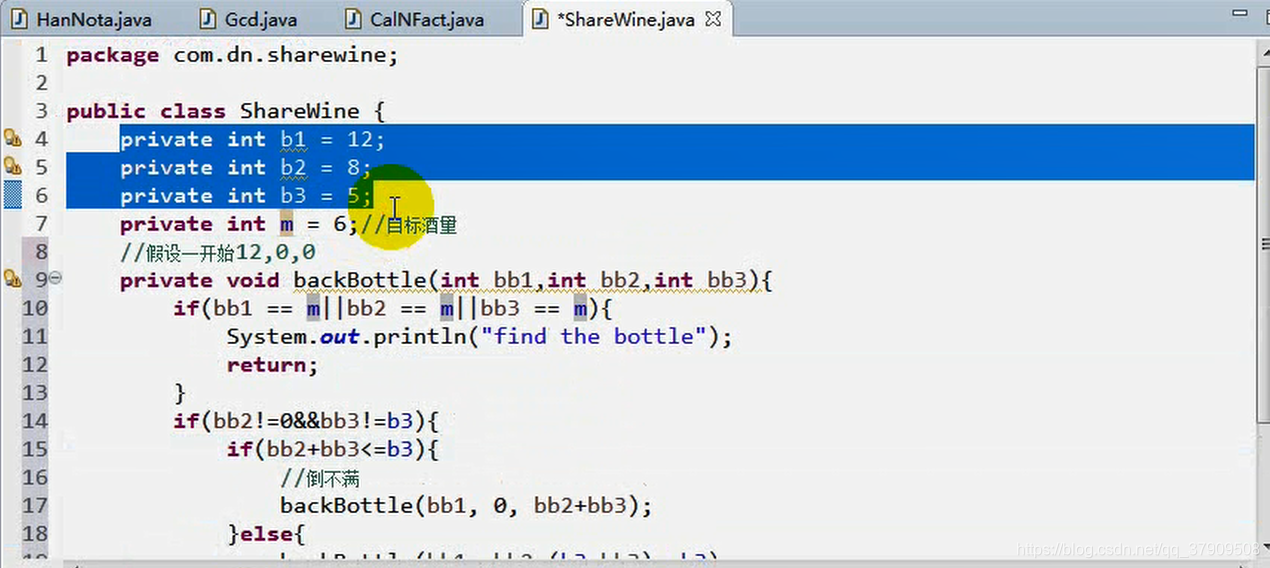
解释：

if（bb2+bb3<=b3）：if（bb2+bb3<=b3）说明bb2和bb3加起来的容量刚好或者还没倒满b3瓶子。这样的话bb2（b2）的里面当前是0，而bb3(b3)里面是他们两个的和。bb1(b1)不发送改变（因为我们没有动它啊）；

else:说明bb2和bb3加起来要大于b3所能盛放的容量。这样的话，b3倒满之后，b2还有剩余，剩余的量bb2-(b3-bb3);

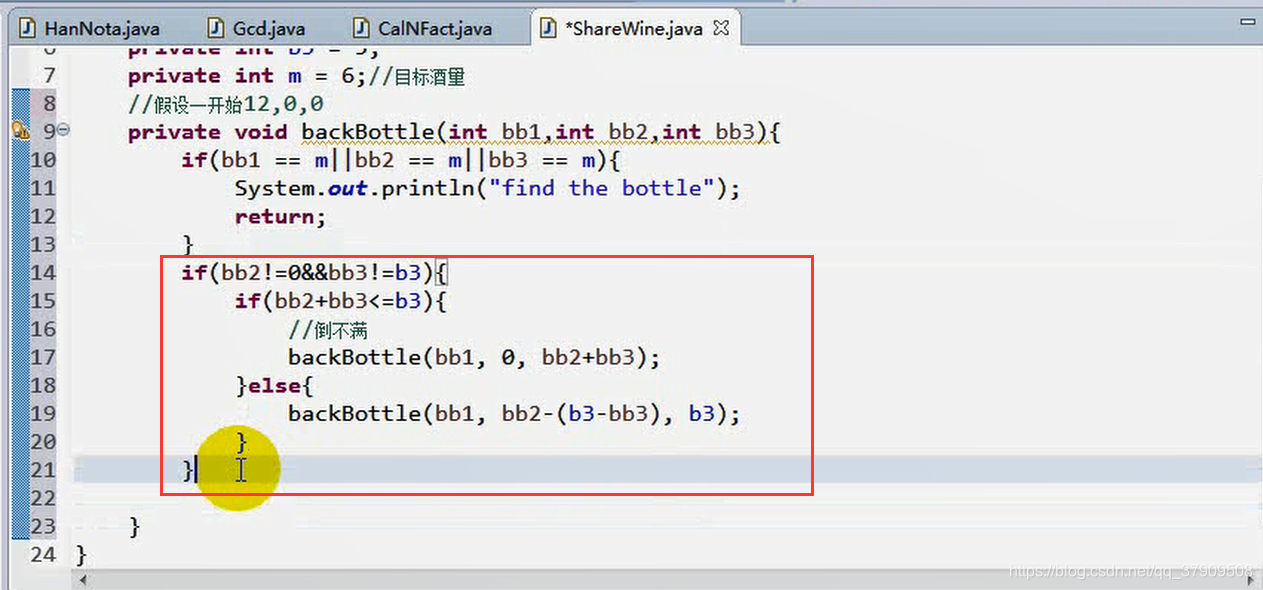
 解释：

if(bb3+bb1<=b1):同理说明倒完后瓶子b1没有满；

else：同理说明倒满了，b3瓶子还有剩余。

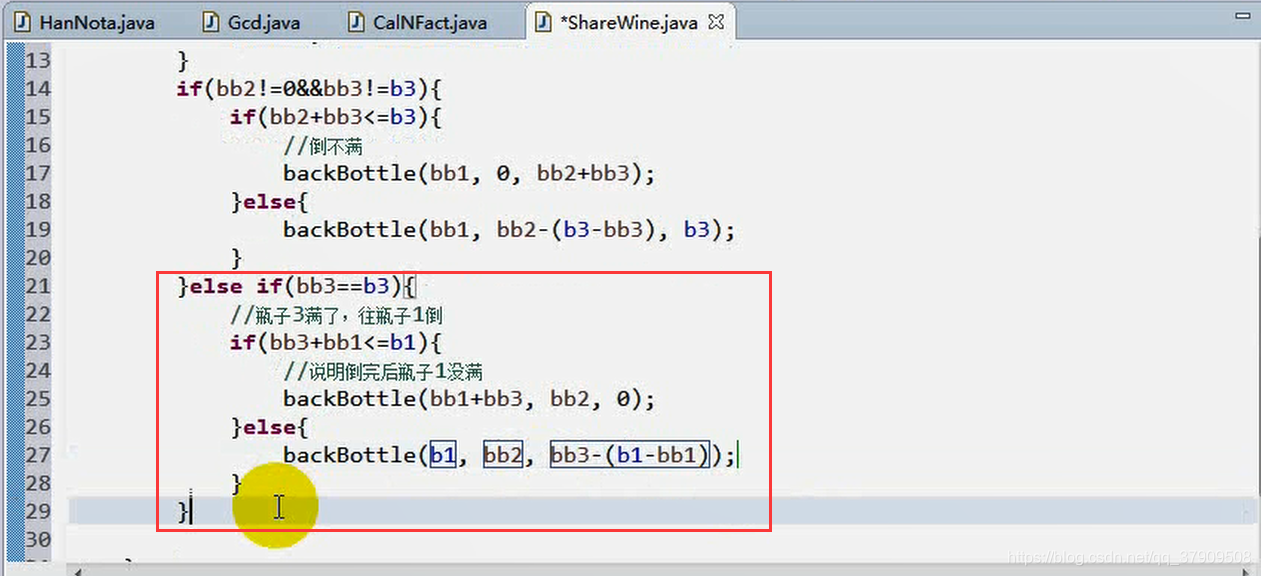
解释：

bb1>=b2：同理，说明b2倒满了，那么b2的当前酒量就是b2，b1的当前的酒量就是bb1-b2

else：同理，说明b2没有倒满，那么bb1里面的酒量为0，bb2里面的容量就是bb1的酒量。

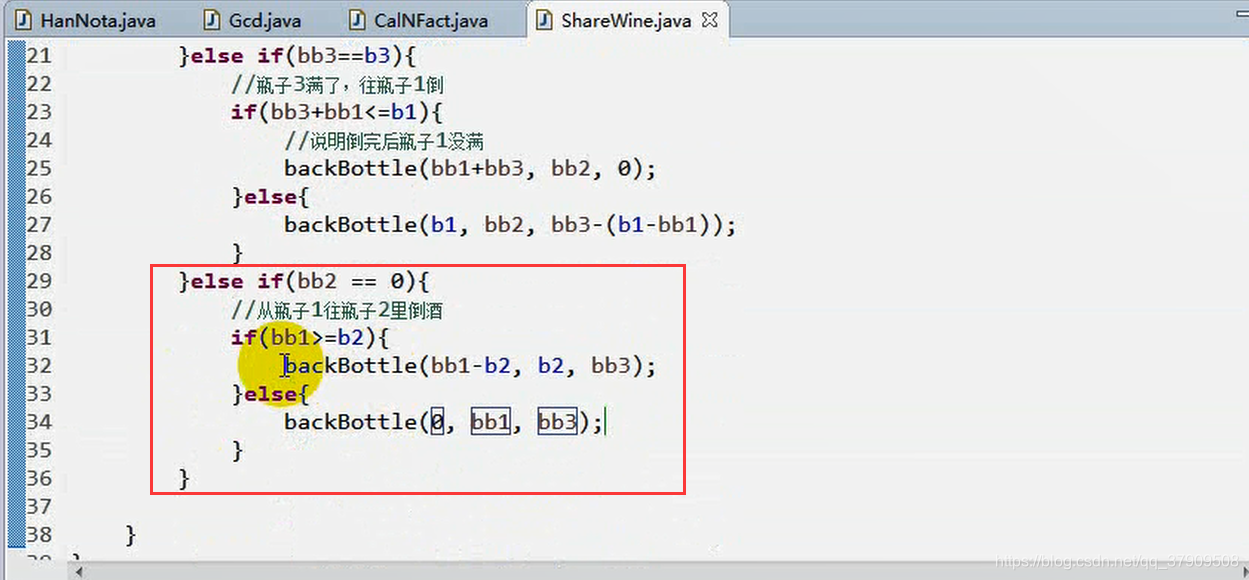
将每次酒杯还存在的酒量结果打出来 

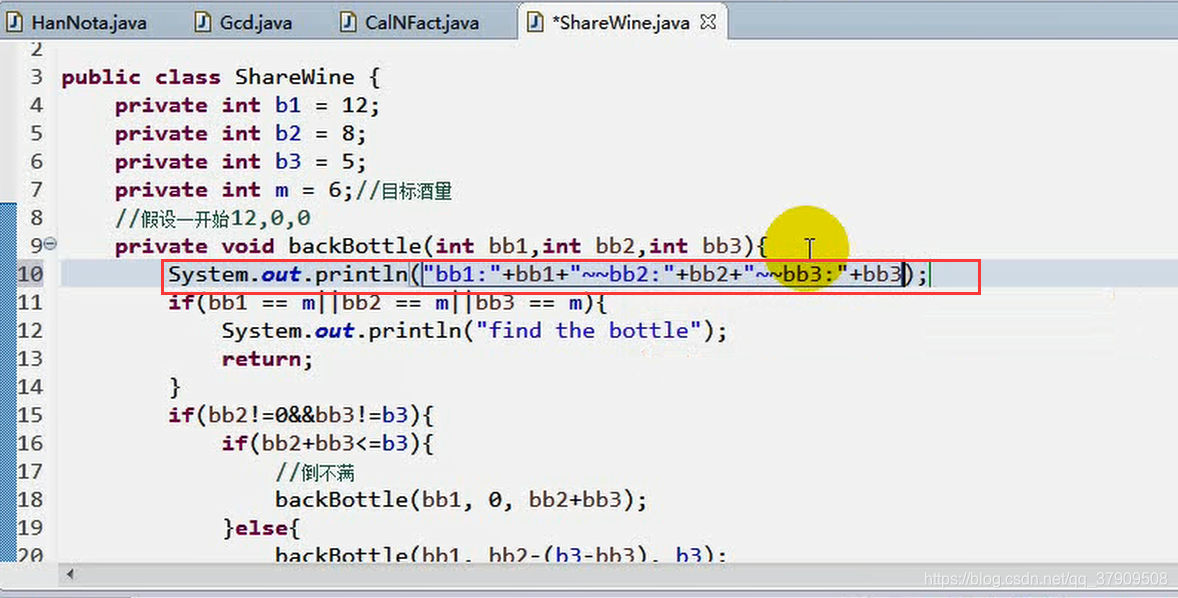
启动程序

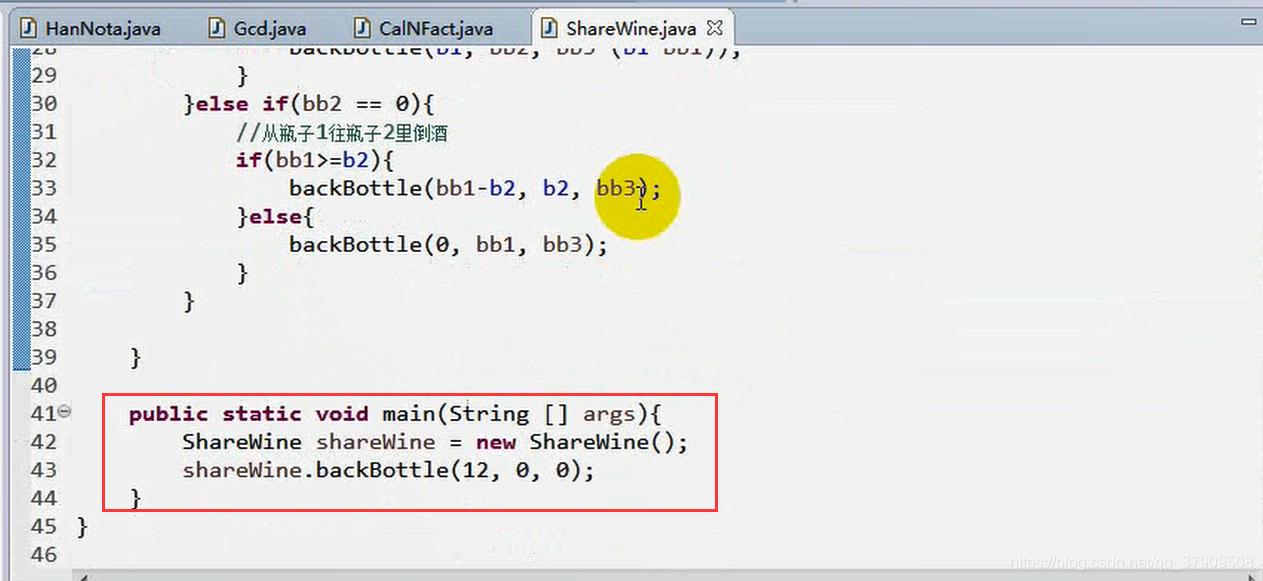
运行结果

贪心算法：

import java.util.Scanner;

/**
 *
 * 取三个瓶子，分别放入3 5 8   量取的时候只需要取两个在它左右两边的即可，例如 取4 的话我们只需要3 6这两个瓶子，
 * 倒满大瓶子，然后倒满小瓶子里面，（判断大瓶子是否已经成立）然后倒掉小瓶子，在把剩下的倒入到小瓶子里面
 * 倒满大瓶子，然后倒满小瓶子里面，（判断大瓶子是否已经成立然后倒掉小瓶子，在把剩下的倒入到小瓶子里面
 */
public class Main1 {
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        int  X = in.nextInt();
        int Y = in.nextInt();
        int Z = in.nextInt();
        int CON = in.nextInt();
        int time=0;
        int[] arr={X,Y,Z};
        insertSort(arr);
        int[] pos = getPos(arr, CON);
        int min=pos[0];
        int max=pos[1];
        int x=0;
        int y=0;
        time=getMin(x,y,min,max,CON,time);
        System.out.print(time);
    }

    private static int[] getPos(int[] arr,int CON) {
        for (int i = 0; i < arr.length-1; i++) {
            if (arr[i]<CON && arr[i+1]>CON){
                return new int[] {arr[i],arr[i+1]};
            }
        }
        return new int[] {0,1};
    }

    public static void insertSort(int[] arr){
        if (arr.length<=1 || arr==null){
            return;
        }
        for (int i = 1; i <arr.length ; i++) {
            for (int j = i-1; j >=0 ; j--) {
                if (arr[j]>arr[j+1]){
                    swap(arr,j,j+1);
                }else {
                    break;
                }
            }
        }
    }
    public static void swap(int[] arr,int L,int R){
        int temp=arr[L];
        arr[L]=arr[R];
        arr[R]=arr[L];
    }

    private static int getMin(int x, int y,int min,int max, int continer,int time) {
        if (x==continer){
            return x;
        }else if (y==continer){
            return y;
        }
        time++;
       y=max;
       y=max-(min-x);
       time++;
       x=min;
       if (y==continer){
           return time;
       }
       time++;
       x=0;
        time++;
       x=y;
        time=getMin(x,y,min,max,continer,time);
       return time;
    }
}
/**
 *
 * 取三个瓶子，分别放入3 5 8   量取的时候只需要取两个在它左右两边的即可，例如 取4 的话我们只需要3 6这两个瓶子，
 * 倒满大瓶子，然后倒满小瓶子里面，（判断大瓶子是否已经成立）然后倒掉小瓶子，在把剩下的倒入到小瓶子里面
 * 倒满大瓶子，然后倒满小瓶子里面，（判断大瓶子是否已经成立然后倒掉小瓶子，在把剩下的倒入到小瓶子里面
 */