机器学习之聚类K-means

一、Cluster analysis

聚类分析提供从单个数据对象到这些数据对象所在的集群的抽象。一些聚类技术根据集群原型来表征每个集群。原型是一个数据对象，代表集群中的其他对象。

二、K-means：

K-means是一种基于原型的聚类技术，它可以创建数据对象的一级分区。
具体而言，K-means根据一组点的质心定义原型。
K均值通常应用于连续n维空间中的对象。

接近度量
要为最近的质心指定一个点，我们需要一个量化“最接近”概念的邻近度量。
欧几里德（L2）距离通常用于欧几里德空间中的数据点。
聚类的目标通常由目标函数表示。
考虑其接近度量是欧几里德距离的数据。
对于测量聚类质量的目标函数，我们可以使用平方误差之和（SSE）。
我们计算每个数据点到其最近质心的欧几里德距离。
然后我们计算平方距离的总和，也称为平方误差之和（SSE）。
较小的SSE值意味着此聚类的原型（质心）更好地表示其聚类中的点。

选择合适的初始质心是基本K-means程序的关键步骤。
一种常见的方法是随机选择初始质心。
随机选择的初始质心可能是不好的选择。
选择合适的初始质心是基本K-means程序的关键步骤。
一种常见的方法是随机选择初始质心。
随机选择的初始质心可能是不好的选择。
这在以下图中说明：

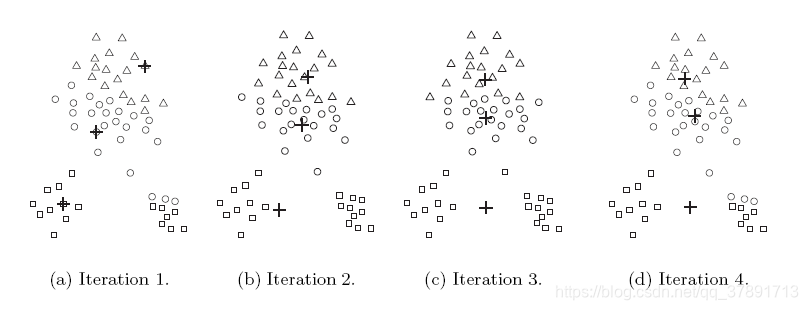
通常用于解决选择初始质心的问题的一种技术是执行多次运行。每次运行使用一组不同的随机选择的初始质心。然后，我们选择具有最小SSE的集群。通常用于解决选择初始质心的问题的一种技术是执行多次运行。每次运行使用一组不同的随机选择的初始质心。然后，我们选择具有最小SSE的集群。

 

当使用欧几里德距离时，异常值可以影响找到的聚类。当存在异常值时，得到的聚类质心可能不像其他情况那样具有代表性。SSE也将更高。因此，发现异常值并事先消除它们通常很有用。为了识别异常值，我们可以跟踪每个点对SSE的贡献。
然后，我们消除那些对SSE贡献异常高的点。我们也可能想要消除小群集，因为它们经常代表异常群。

两种通过增加簇数来降低SSE的后处理策略是：
1.拆分群集,通常选择具有最大SSE的群集。
2.引入一个新的集群质心,通常选择距离其相关联的群集中心最远的点。
如果我们跟踪每个点对SSE的贡献，我们就可以确定这一点。

两种减少集群数量的后处理策略，同时试图最小化总SSE的增加
分散群集:
这是通过移除与群集对应的质心来实现的,然后将该群集中的点重新分配给其他群集。分散的集群应该是增加总SSE最少的集群。
合并两个集群:
我们可以合并导致总SSE增幅最小的两个集群。

平分K均值法：Bisecting K-means

Bisecting K-means算法是基本K-means算法的扩展。
该算法的主要步骤描述如下：
要获得K个簇，请将所有点的集合拆分为两个簇。
选择要拆分的其中一个集群。
继续该过程，直到生成K簇。

有多种不同的方法可以选择要拆分的群集。
我们可以在每一步选择最大的集群。
我们也可以选择SSE最大的那个。
我们还可以使用基于大小和SSE的标准。
不同的选择导致不同的集群。
我们经常使用它们的质心作为基本K-means算法的初始质心来细化所得到的聚类。
二等分K-means算法如下图所示：

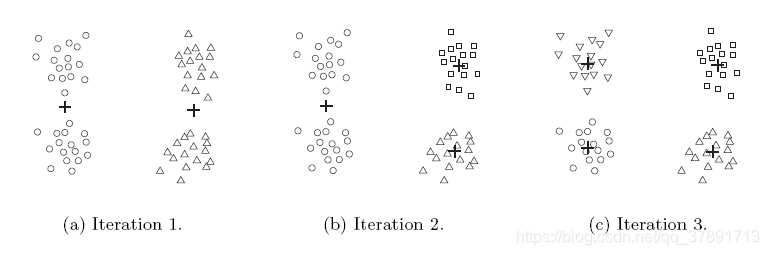
Limitations of K-means：

K-means及其变体在寻找不同类型的簇方面具有许多限制。
特别是，K-means难以检测具有非球形形状或大小不同的尺寸或密度的簇。
这是因为K-means被设计用于寻找具有相似大小和密度的球状星团，或者是分离良好的星团。
这在以下示例中说明：

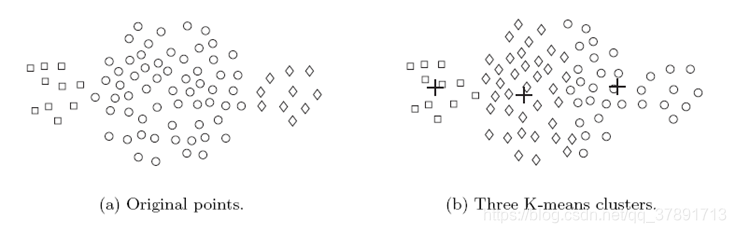
在这个例子中，K-means找不到三个自然聚类，因为其中一个聚类比另外两个聚类要大得多。
结果，最大的集群被划分为子集群。
同时，其中一个较小的集群与最大集群的一部分组合在一起。

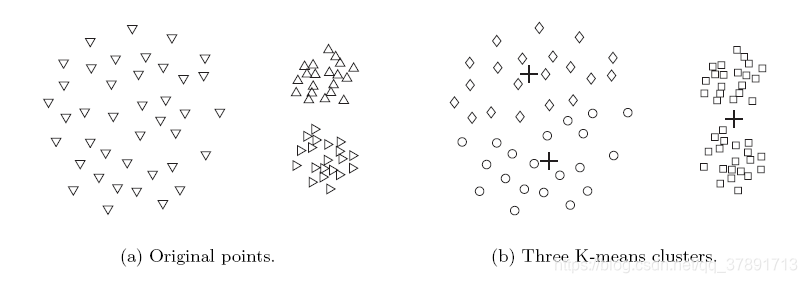
在这个例子中，K-means无法找到三个自然聚类。
这是因为两个较小的簇比最大的簇密集得多。

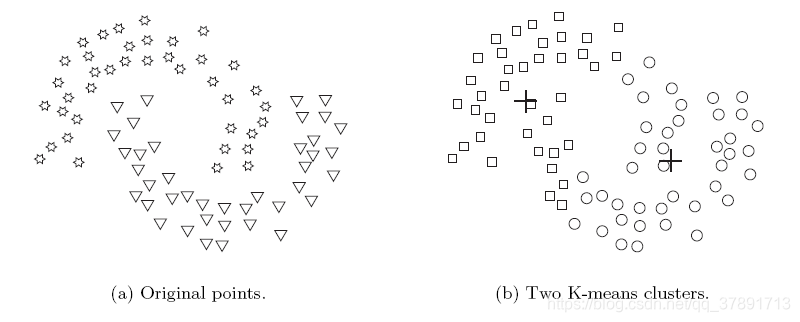
在该示例中，K-means找到两个群集，其混合两个自然群集的部分。
这是因为天然星团的形状不是球状的。