目录
一、选题展示
题B5:搜索树操作程序
开发建立搜索树的程序,在程序中可以进行参数设置、数据元素输入与操作选择,支持搜索树结构中的各种数据操作(如插入、删除、搜索等),可使用C、C++或Java等编程语言实现。
基本要求
(1) 连续输入若干数据元素,程序自动在画板上画出相应二叉搜索树;可以对已经生成的二叉搜索树进行插入、删除和搜索操作,程序动态显示操作结果。
(2) 连续输入若干数据元素,在画板上画出相应二叉平衡树;可以对已经生成的二叉平衡树进行插入、删除和搜索操作,程序动态显示操作结果。
(3) 实物演示时要求演示结果正确。
(4) 程序操作友好、健壮。
提高要求:
(1) 连续输入若干数据元素,程序能动态画出相应B-树。
(2) 可以对已经生成的B-树进行插入、删除和搜索操作,程序动态显示操作结果。
(3) 图形化界面,树形美观对称。
二、思考题目
个人对“动态”的理解
模仿终端的形式,在c语言的输入框里,通过“add XX”、“delete XX”、“find XX”进行插入、删除和搜索操作,每次输入后,都会输出二叉平衡树/B-树,输入“quit”退出程序。
根据题目要求,将整个项目划分为以下阶段:
阶段一:图形显示二叉搜索树之插入
阶段二:图形显示二叉搜索树之查删
阶段三:动态显示二叉搜索树
阶段四:加入调整规则使二叉搜索树变为平衡树
阶段五:动态显示二叉平衡树
阶段六:使用多种方式显示二叉平衡树
阶段七:图形显示B-树
阶段八:动态显示B-树
图形展示参考:二叉树的图形显示
三、阶段一:图形显示二叉搜索树之插入
1.图形显示二叉搜索树的要求
-
层次化输出:同层次遍历,但是需要在每层输出完毕后进行换行。可由层数和孩子节点的关系2^(n-1)类推出所有层的节点总数,待输入完毕后,进行自动按层换行。
-
确定相对位置:安排节点位置用以直观的得到节点之间的关系,使用如下思路:在节点类型中增加成员变量int pos,用以表示节点所在位置。如果父节点为P,位置为P.pos,则可在下一层中,令左孩子L的位置满足如下关系L.pos=P.pos-1,右孩子R的位置满足R.pos=P.pos+1,是根节点位置为一个大小适宜的正数M,则可避免子树中节点位置出现负数的情况。
-
输出冲突:不同双亲节点的子节点可能出现位置重叠的情况:
对已一个节点P,定义它的左子树中的结点pos最大值设为LMax(P),右子树中节点pos最小值为RMin(P)。 输出一棵树时不会有冲突的充分条件是对于每一个结点P都有:LMax(P) < P.pos < RMin(P),也就是所有左子树中的结点都在根节点的左方,所有右子树中的结点都在根结点的右方。
如果某一结点不满足LMax(P)<P.pos,就将P和右子树中的左右结点都右移LMax(P) - P.max + 1个位置。如果不满足P.pos < RMin(P),就将右子树右移RMin(P)-P.pos + 1个位置。具体的处理过程是这样的:按照层次遍历的顺序,自上到下、自左向右地检查每个结点是否和左、右子树存在冲突,如果存在,就移动P和右子树。
移动之后有两种情况,一种是结点P是其父节点(PP)的左孩子,这是P和P的右子树都属于PP的左子树,移动P和P的右子树有可能会造成条件LMax(PP) < P.pos的失败,所以这个时候需要对PP再进行一次冲突判断,这样递归向上知道没有冲突。第二种情况是P是PP的右孩子,这种情况下移动P和右子树肯定不会造成PP的冲突。在P的祖父节点中,设第一个具有左孩子的节点为A,移动P和P的右子树有可能造成A的冲突,需要再对A进行冲突处理。
2.代码和输出
InfoH.h
用于定义二叉树节点所要继承的类,如上所说,定义了表示位置的成员变量pos。
struct InfoH {
int pos;
bool newline;
InfoH() : pos(INFI), newline(false) {}
int add_pos(int add) {
pos += add;
return pos;
}
};PosSetter.h
引用InfoH.h文件,初始化二叉树中每个节点的成员变量pos,在函数VisualTree::draw()中被调用。
#include "InfoH.h"
template<class TreeNode>
class PosSetter
{
public:
PosSetter(TreeNode* TreeNode::* p, TreeNode *TreeNode::* l, TreeNode *TreeNode::* r) :
parent(p), left(l), right(r)
{
}
void operator() (TreeNode *node)
{
TreeNode *p = node->*parent;
if (p != NULL) {
if (node == p->*left) { node->pos = p->pos - 1; }
if (node == p->*right) { node->pos = p->pos + 1; }
}
}
private:
TreeNode *TreeNode:: *parent;
TreeNode *TreeNode:: *left;
TreeNode *TreeNode:: *right;
};
PosAdder.h
用以调整节点的pos值,调整值在实例化对象的时候进行指定,每个对象对应一个值。
#include "InfoH.h"
class PosAdder
{
public:
PosAdder(int n_) : n(n_) {}
int operator() (InfoH *node) { return node->add_pos(n); }
private:
int n;
};
ExtremumGetter.h
遍历结点的时候, 记录下节点中的极值。
template<class TreeNode>
class ExtremumGetter
{
public:
ExtremumGetter(TreeNode *min = 0, TreeNode *max = 0) {
init(min, max);
}
void operator() (TreeNode *p) {
if ((min_ && p->pos < min_->pos) || !min_) { min_ = p; }
if ((max_ && p->pos > max_->pos) || !max_) { max_ = p; }
}
void init(TreeNode *min, TreeNode *max) {
min_ = min; max_ = max;
if (min_ && max_ && max_->pos < min_->pos) {
std::swap(min_, max_);
}
}
TreeNode *min() const { return min_; }
TreeNode *max() const { return max_; }
private:
TreeNode *min_;
TreeNode *max_;
};
以上三个文件中定义的三个类都重载了operator (),他们都是在调用VisualTree::traverse_level()的时候最为函数对象被调用的。
VisualTree.h
#include <cassert>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <queue>
#include "ExtremumGetter.h"
#include "PosAdder.h"
#include "PosSetter.h"
#include "TreePrinter.h"
struct IntExtremumPair {
int min;
int max;
IntExtremumPair(int rh1 = 0, int rh2 = 0) : min(rh1), max(rh2) {}
};
template<class TreeNode, class ValueType>
class VisualTree
{
public:
typedef TreeNode *TreeNode::* PtrToMember;
typedef ValueType TreeNode::* PtrToData;
VisualTree(PtrToMember p, PtrToMember lc, PtrToMember rc, PtrToData val);
void draw(TreeNode *node, const char *promot = NULL);
private:
void adjust_pos(TreeNode *root);
TreeNode* ancestor(TreeNode *node);
int digits(int n);
int digits(char c);
int digits(const char*s);
IntExtremumPair extreme_pos(TreeNode *p);
ExtremumGetter<TreeNode> extreme_node(TreeNode *root);
int scan_tree(TreeNode *root);
template<class VST> void traverse_level(TreeNode *p, VST &vst);
ExtremumGetter<TreeNode> getter;
TreePrinter<TreeNode, ValueType> printer;
PosSetter<TreeNode> setter;
PtrToMember parent, left, right;
ValueType TreeNode:: *value;
};
/*
* 构造函数
*/
template<class TreeNode, class ValueType>
VisualTree<TreeNode, ValueType>::VisualTree(PtrToMember p, PtrToMember lc, PtrToMember rc, PtrToData val) :
getter(), printer(p,lc,rc,val), setter(p,lc,rc), parent(p), left(lc), right(rc), value(val)
{
}
/*
* 越界调整
*/
template<class TreeNode, class ValueType>
void VisualTree<TreeNode, ValueType>::adjust_pos(TreeNode *root)
{
if (root == NULL) {
return;
}
int diff = 0;
IntExtremumPair extr;
if (root->*left) {
extr = extreme_pos(root->*left);
if (root->pos <= extr.max) { // 左子树越界:将根节点右移及其右子树右移
diff = extr.max - root->pos + 1;
PosAdder adder(diff);
root->add_pos(diff);
traverse_level(root->*right, adder);
adjust_pos(ancestor(root));
}
}
if (root->*right) { // 右子树越界:将右字树右移
extr = extreme_pos(root->*right);
if (extr.min <= root->pos) {
diff = root->pos - extr.min + 1;
PosAdder adder(diff);
traverse_level(root->*right, adder);
adjust_pos(ancestor(root));
}
}
}
/*
* 寻找节点node的第一个具有左孩子的祖先
* @return 祖先地址或者NULL
*/
template<class TreeNode, class ValueType>
TreeNode *VisualTree<TreeNode, ValueType>::ancestor(TreeNode *node)
{
TreeNode *pchild = node;
TreeNode *pparent = node->*parent;
while (pparent && pchild == pparent->*right) {
pchild = pparent;
pparent = pchild->*parent;
}
return pparent;
}
/*
* 计算一个整数n输出时占用的字符数
* @return 整数n输出时所占字符数
*/
template<class TreeNode, class ValueType>
int VisualTree<TreeNode, ValueType>::digits(int n)
{
int len = 0;
if (n < 0) {
len++;
n = -n;
}
do {
len++;
n /= 10;
} while (n);
return len;
}
/*
* 输出一个字符所占用的字符数
* @return 1
*/
template<class TreeNode, class ValueType>
int VisualTree<TreeNode, ValueType>::digits(char c)
{
return 1;
}
/*
* 输出一个字符串所占用的字符数
* @return 字符串长度
*/
template<class TreeNode, class ValueType>
int VisualTree<TreeNode, ValueType>::digits(const char *s)
{
return strlen(s);
}
/*
* 图形化显示二叉树
* @input root:树的根节点,promot:可选提示信息,应以'\0'结尾
*/
template<class TreeNode, class ValueType>
void VisualTree<TreeNode, ValueType>::draw(TreeNode *root, const char *promot)
{
if (promot) {
printf("%s\n", promot);
}
if (root == NULL) {
printf("Empty tree!\n");
return;
}
int len = scan_tree(root);
printer.set_edge_length(len);
traverse_level(root, printer);
}
/*
* 获得最靠左和最靠右的两个节点指针
* @return std::pair, 其中first指向最左节点,second指向最右节点
*/
template<class TreeNode, class ValueType>
ExtremumGetter<TreeNode>
VisualTree<TreeNode, ValueType>::extreme_node(TreeNode *node)
{
getter.init(node, node);
traverse_level(node, getter);
return getter;
}
/*
* 获得最靠左的节点和最靠右的节点pos
* @return 包含最小/最大位置坐标的IntExtremumPair
*/
template<class TreeNode, class ValueType>
IntExtremumPair VisualTree<TreeNode, ValueType>::extreme_pos(TreeNode *node)
{
ExtremumGetter<TreeNode> nodes = extreme_node(node);
IntExtremumPair ret;
if (nodes.min()) { ret.min = nodes.min()->pos; }
if (nodes.max()) { ret.max = nodes.max()->pos; }
return ret;
}
/*
* 扫描整棵树,设置相关信息(换行标记/数据位数)
* @return 最大数据位数
*/
template<class TreeNode, class ValueType>
int VisualTree<TreeNode, ValueType>::scan_tree(TreeNode *root)
{
int cnt; // 当前深度已扫描节点个数
int depth; // 当前扫描深度
int max_len;
std::queue<TreeNode*> qnode;
std::vector<int> num_node; // num_node[i]: 深度为i的节点总数
num_node.push_back(1); // 一个根节点
num_node.push_back(0); // 初始化第1层
qnode.push(root);
// 将根节点位置设为0,据此算出其他节点相对位置
root->pos = 0;
traverse_level(root, setter);
// 获取最左最右坐标
IntExtremumPair extr = extreme_pos(root);
// 将最左节点坐标调整为0,其他节点整体右移
PosAdder adder(root->pos - extr.min);
traverse_level(root, adder);
cnt = 0; depth = 0; max_len = 0;
for ( ; !qnode.empty(); qnode.pop()) {
TreeNode *temp = qnode.front();
adjust_pos(temp);
if (temp->*left) {
qnode.push(temp->*left);
num_node[depth+1]++;
}
if (temp->*right) {
qnode.push(temp->*right);
num_node[depth+1]++;
}
if (++cnt == num_node[depth]) {
temp->newline = true;
depth++;
num_node.push_back(cnt = 0); // 初始化下下层节点个数
} else {
temp->newline = false;
}
max_len = std::max(max_len, digits(temp->*value));
}
// 使树和屏幕左侧之间不留空隙
extr = extreme_pos(root);
if (extr.min > 0) {
PosAdder adder(-extr.min);
traverse_level(root,adder);
}
return max_len;
}
/*
* 层次遍历二叉树,对树中每个节点执行操作vst
*/
template<class TreeNode, class ValueType>
template<class VST>
void VisualTree<TreeNode, ValueType>::traverse_level(TreeNode *root, VST &vst)
{
if (root == NULL) {
return;
}
TreeNode *temp;
std::queue<TreeNode*> qnode;
for (qnode.push(root); !qnode.empty(); qnode.pop()) {
temp = qnode.front();
vst(temp);
if (temp->*left) { qnode.push(temp->*left); }
if (temp->*right) { qnode.push(temp->*right); }
}
}
TreePrinter.h
template<class TreeNode, class ValueType>
class TreePrinter
{
public:
typedef TreeNode *TreeNode::*PtrToMember;
typedef ValueType TreeNode::*PtrToData;
TreePrinter(PtrToMember p, PtrToMember l, PtrToMember r, PtrToData d) :
edge_len(2), num_out(0), vec(), parent(p), left(l), right(r), value(d)
{
}
void set_edge_length(int len)
{
edge_len = std::max(len, 2); // 边沿最小宽度为2
}
void operator() (TreeNode *node)
{
assert(node);
TreeNode *lc = node->*left;
TreeNode *rc = node->*right;
int lbl = 0, rbl = 0; // 左边沿字符长度,右边沿字符长度
int spaces = node->pos * edge_len - num_out; // 占位空白字符数
if (lc) { lbl = edge_len * (node->pos-(node->*left)->pos) - 1; }
if (rc) { rbl = edge_len * ((node->*right)->pos-node->pos) - 1; }
spaces -= lbl;
assert(spaces >= 0);
while (spaces--) {
num_out += printf(" ");
}
if (node->*left) {
vec.push_back(num_out-1);
while (lbl--) {
num_out += printf("_");
}
}
num_out += out_value(node->*value);
if (node->*right) {
while (rbl--) {
num_out += printf("_");
}
vec.push_back(num_out);
}
if (node->newline) {
new_line();
}
}
private:
int out_value(char c) { return printf("%c", c); }
int out_value(int i) { return printf("%d", i); }
int out_value(const char *p) { return printf("%s", p); }
void new_line()
{
printf("\n");
if (!vec.empty()) {
int n = 0, end = vec[vec.size()-1];
for (int i = 0; i <= end && n < (int)vec.size(); ++i) {
if (i == vec[n]) {
printf("|");
n++;
} else {
printf(" ");
}
}
}
printf("\n");
num_out = 0;
vec.clear();
}
int edge_len;
int num_out; // 已输出字符数
std::vector<int> vec;
PtrToMember parent;
PtrToMember left;
PtrToMember right;
ValueType TreeNode:: *value;
};
bst.h 为了方便测试写的一个Binary Search Tree,在main.cc中想BST中随机插入一定数量的结点,然后显示:
#include <cassert>
#include <algorithm> // swap
#include "InfoH.h"
#define IS_ROOT(p) ((p)->parent == NULL)
#define IS_LEAT(p) ((p)->left == NULL && (p)->right == NULL)
#define IS_LEFT(p) (!IS_ROOT(p) && (p) == (p)->parent->left)
#define IS_RIGHT(p) (!IS_ROOT(p) && (p) == (p)->parent->right)
template<typename T>
struct TreeNode : public InfoH {
T val;
TreeNode *parent;
TreeNode *left;
TreeNode *right;
TreeNode(const T &v) : InfoH(), val(v), parent(0), left(0), right(0) {}
TreeNode(const T &v, TreeNode *p) : InfoH(), val(v), parent(p), left(0), right(0) {}
};
template<typename T>
class BSTree
{
public:
/*
* 构造函数
*/
BSTree() : root_(0) {}
/*
* 析构函数
*/
virtual ~BSTree()
{
while (!empty()) {
remove(root_);
}
}
/*
* 判断树是否为空
* @return true:空, false:非空
*/
bool empty()
{
return root_ == NULL;
}
/*
* 插入一个新节点
* @return 新插入节点地址
*/
TreeNode<T> *insert(const T &val)
{
if (root_ == NULL) {
return root_ = new TreeNode<T>(val);
}
TreeNode<T> *parent = root_;
TreeNode<T> *hole = 0;
hole = (root_->val < val ? root_->right : root_->left);
while (hole != NULL) {
parent = hole;
hole = (hole->val < val ? hole->right : hole->left);
}
if (parent->val < val) {
return parent->right = new TreeNode<T>(val, parent);
} else {
return parent->left = new TreeNode<T>(val, parent);
}
}
/*
* 寻找值为x的节点
* @reutrn 节点地址,如果不存在返回NULL
*/
TreeNode<T> *find(T &x)
{
TreeNode<T> *temp = root_;
while (temp != NULL) {
if (temp->val == x) {
break;
}
temp = (temp->val < x ? temp->right : temp->left);
}
// temp == NULL
return temp;
}
/*
* 删除指定节点
*/
void remove(TreeNode<T> *p)
{
assert(p != NULL);
TreeNode<T> *temp = NULL;
if (p->left && p->right) { // 有两个孩子
TreeNode<T> *temp = succ(p);
std::swap(p->val, temp->val); // 交换和后继节点的内容
remove(temp); // 删除后继节点
} else if (p->left || p->right) { // 只有一个孩子
temp = (p->left ? p->left : p->right);
if (IS_ROOT(p)) {
root_ = temp;
root_->parent = NULL;
} else if (IS_LEFT(p)) {
p->parent->left = temp;
temp->parent = p->parent;
} else {
p->parent->right = temp;
temp->parent = p->parent;
}
delete p;
} else { // 没有孩子
if (IS_ROOT(p)) {
root_ = NULL;
} else if (IS_LEFT(p)) {
p->parent->left = NULL;
} else {
p->parent->right = NULL;
}
delete p;
}
}
/*
* 返回根节点地址
*/
TreeNode<T> *root() const
{
return root_;
}
private:
/*
* 寻找最小节点
* @reutrn 最小节点地址
*/
TreeNode<T> *min_node(TreeNode<T> *p)
{
assert(p != NULL);
TreeNode<T> *temp = p;
while (temp->left != NULL) {
temp = temp->left;
}
return temp;
}
/*
* 寻找最大节点
* @return 最大节点地址
*/
TreeNode<T> *max_node(TreeNode<T> *p)
{
assert(p != NULL);
TreeNode<T> *temp = p;
while (temp->right != NULL) {
temp = temp->right;
}
return temp;
}
/*
* 寻找指定节点p的后继节点(比p节点大的所有节点中的最小节点)
* @return 后继节点地址
*/
TreeNode<T> *succ(TreeNode<T> *p)
{
assert(p != NULL);
if (p->right) { // 节点有右子树:右子树中最小节点即为后继节点
return min_node(p->right);
}
// else
TreeNode<T> *child = p;
TreeNode<T> *father = p->parent;
while (father && !IS_LEFT(child)) { // 节点无右子树:第一个有左孩子的祖先节点即为后继节点
child = father;
father = child->parent;
}
return father;
}
TreeNode<T> *root_;
};
main.c
#include <iostream>
#include <vector>
#include "bst.h"
#include "VisualTree.h"
int main(int argc, char*argv[])
{
typedef int ValueType;
typedef TreeNode<ValueType> NodeType;
BSTree<ValueType> tree;
VisualTree<NodeType, ValueType> vtree(&NodeType::parent,
&NodeType::left,
&NodeType::right,
&NodeType::val);
int num = 15;
srand(time(NULL));
for (int i = 0; i < num; ++i) {
ValueType v = rand() % 1000; // 随机生成一个[0,1000)的数
tree.insert(v);
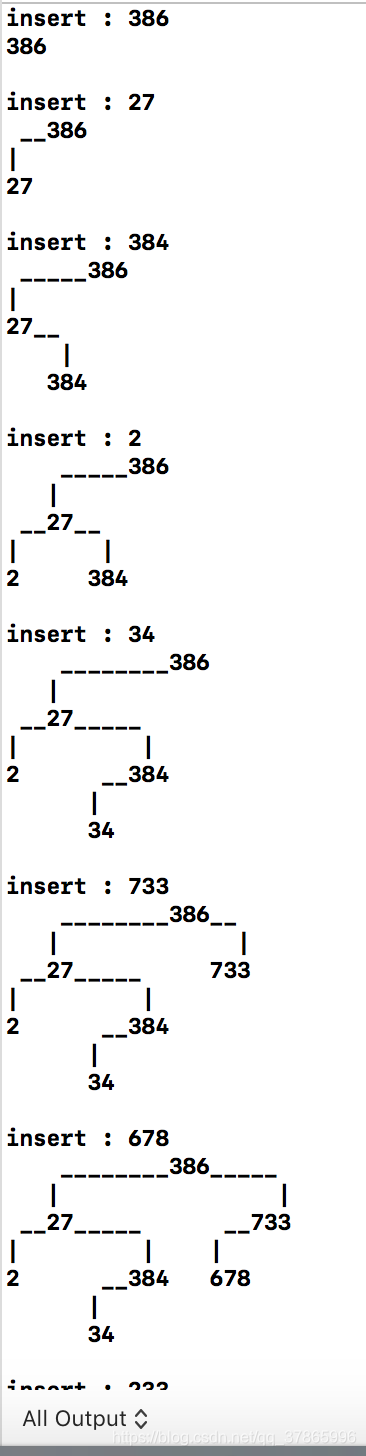
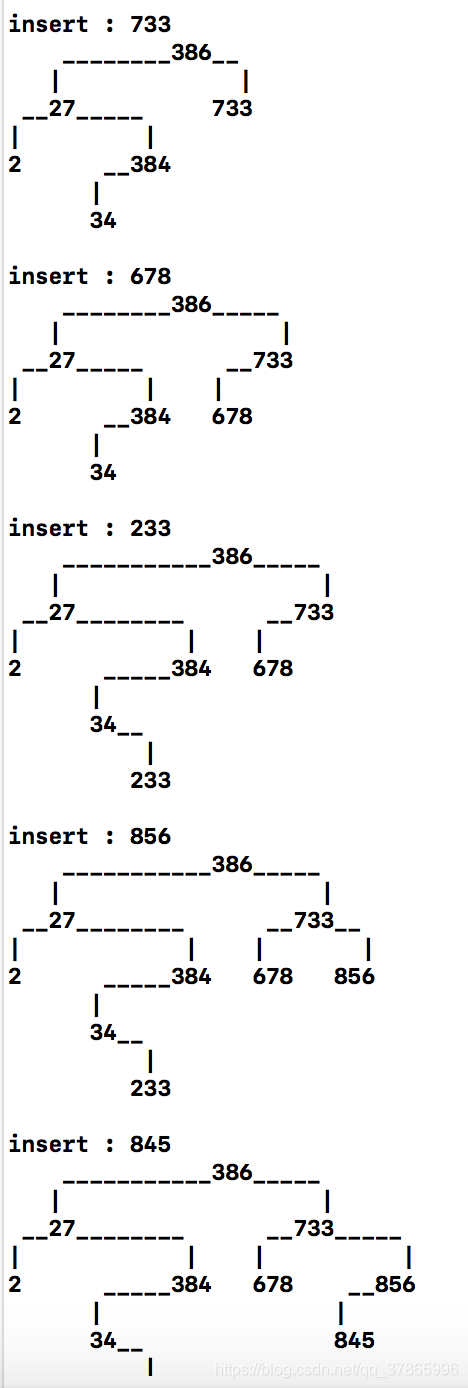
std::cout << "insert : " << v << std::endl;
vtree.draw(tree.root());
}
return 0;
}
对博文的引用即到这里,下面就是自己的思考和探索了。这位博主是很666的,想到当年输出个*组成的大红心就费了好大劲,不得不给他点个赞啦哈哈。
程序运行结果:
四、阶段二:图形显示二叉搜索树之查删
1.二叉搜索树的查找操作
根据二叉搜索树的特点,将待查找的值和根节点进行比较,小于根节点就前往左子树查找,大于根节点前往右子树查找,等于根节点即为查找结果。返回的结果"已找到",如果不存在返回“未找到”
可在main.c进行输出值的判断:
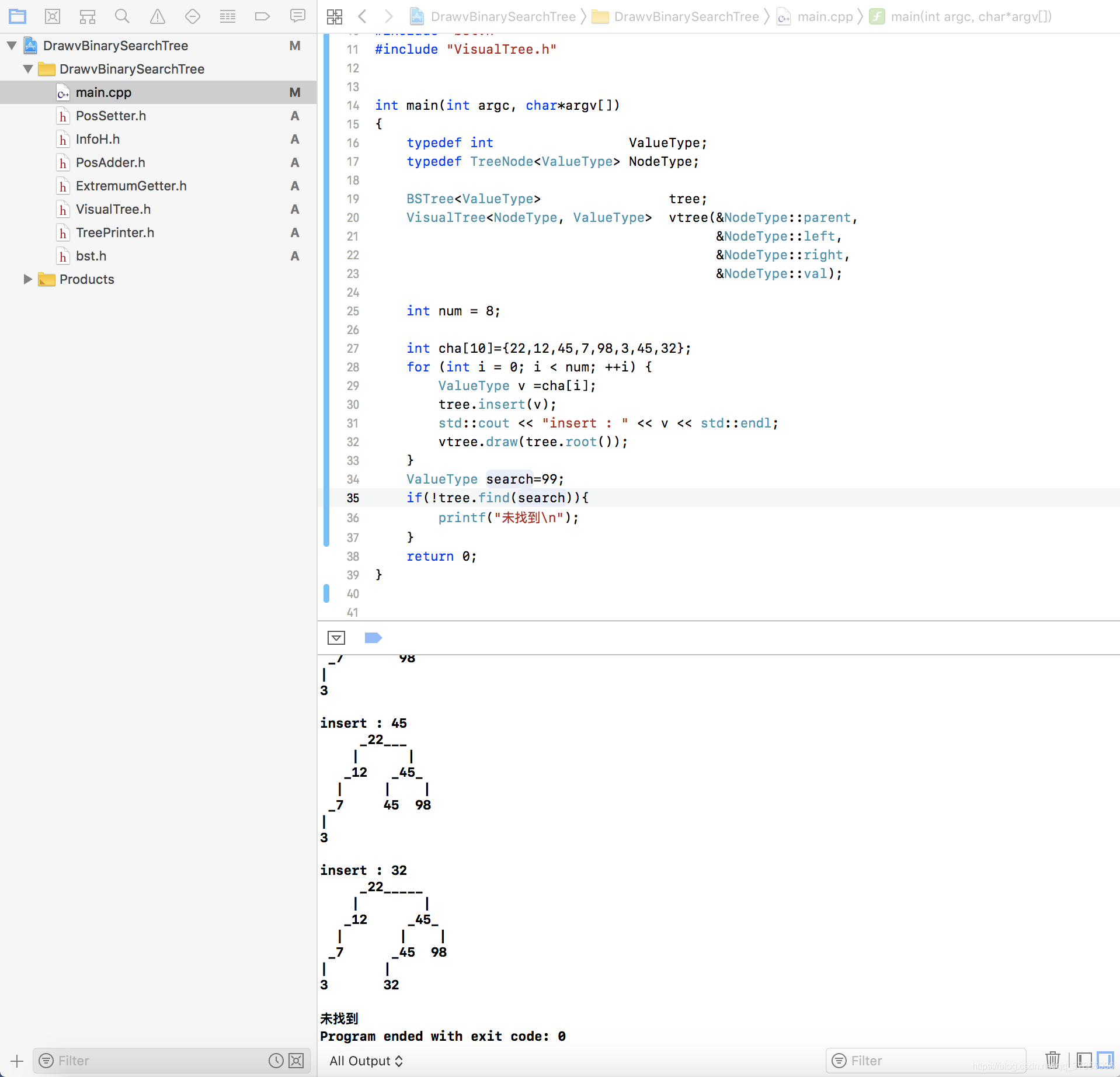
ValueType search=99;
if(!tree.find(search)){
printf("未找到\n");
}
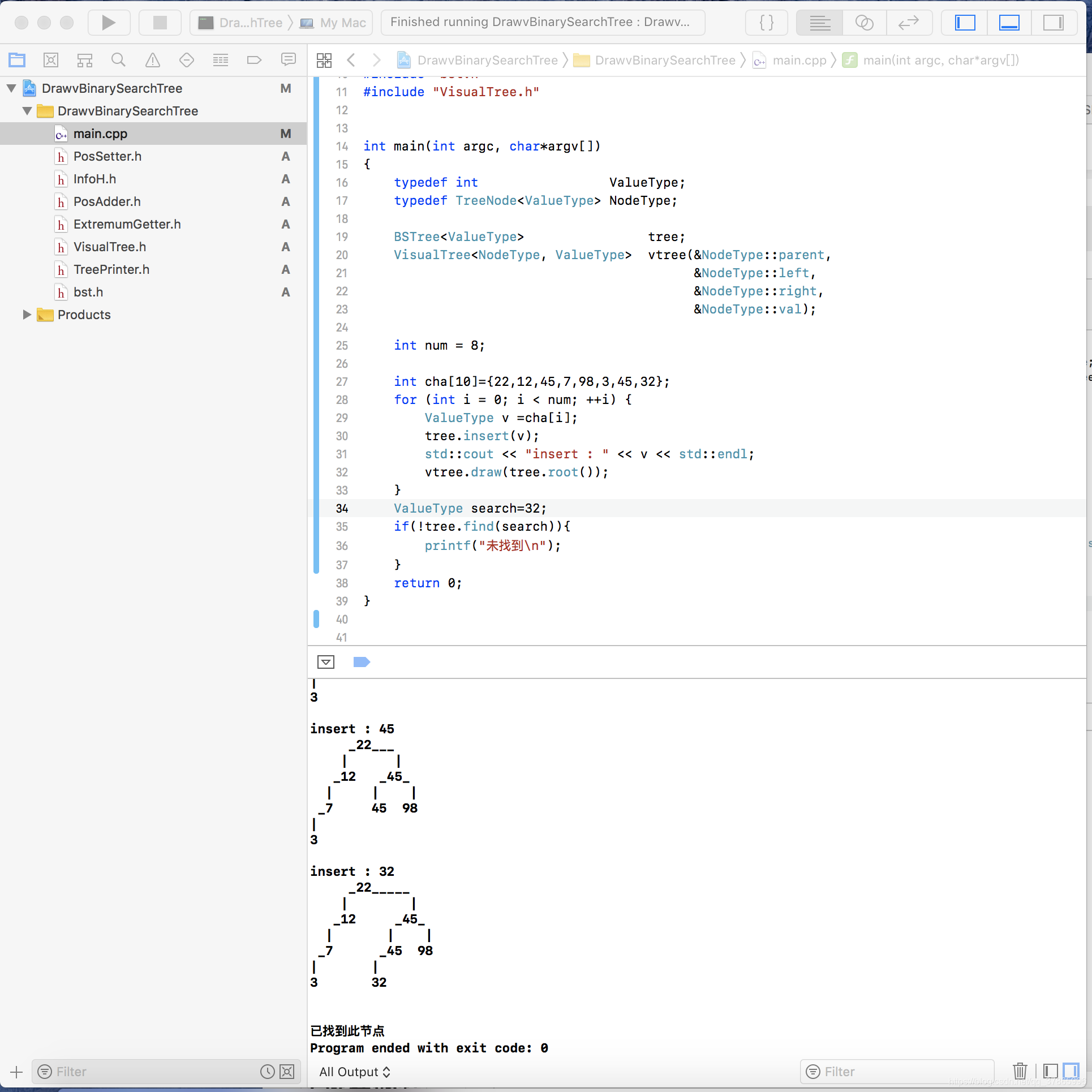
2.二叉搜索树的删除操作
在查找基础上进行删除,最后再次显示:

五、阶段三:动态显示二叉搜索树
就我个人的理解来说,动态就是,像命令行一样,输入指令进行动态的增删改查,并输出结果。
在main.c函数中进行修改:
int t=100;//预设最多操作100次
int m=0,n=0;
while(t){
printf("-----------------------------------------------\n");
printf("--------------------请输入指令-------------------\n");
printf("--- 插入:1,num 查找:2,num ---\n");
printf("--- 删除:3,num 退出:4 ---\n");
printf("--- (注:num设定为0~100) ---\n");
printf("-----------------------------------------------\n");
scanf("%d,%d",&m,&n);
printf("\n-----------------------------------------------\n");
//健壮性1
if(m!=1&&m!=2&&m!=3&&m!=4){
printf("输入指令错误,请重新输入。\n");
continue;
}
//健壮性2
if(n<0||n>100){
printf("输入数字错误,请重新输入。\n");
continue;
}
if(m==1){
ValueType v =n;
tree.insert(v);
std::cout << "insert : " << v << std::endl;
vtree.draw(tree.root());
}else if (m==2){
ValueType search =n;
if(!tree.find(search)){
printf("未找到\n");
}else{
printf("已找到\n");
}
}else if(m==3){
ValueType search=n;
if(!tree.find(search)){
printf("未找到\n");
}else{
printf("已找到,并删除\n");
}
TreeNode<int> *p=tree.find(search);
tree.remove(p);
vtree.draw(tree.root());
}else if(m==4){
break;
}
t--;
}
return 0;执行效果:
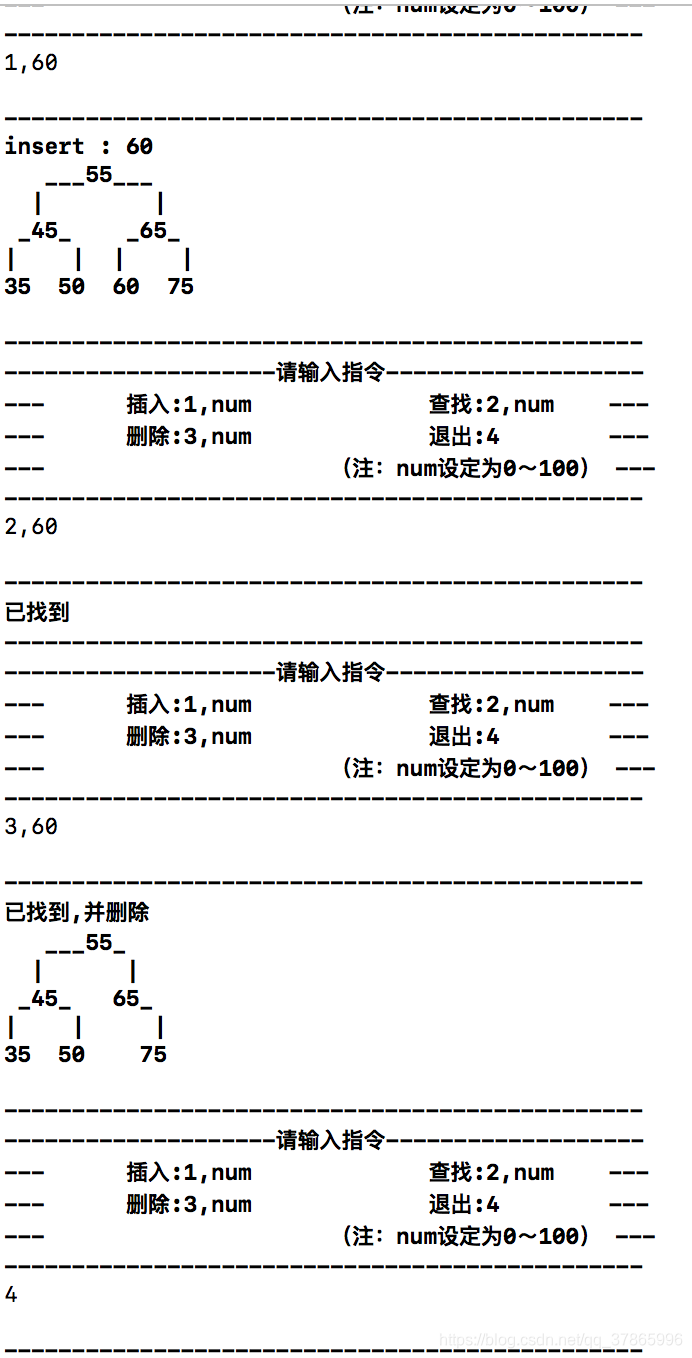
错误输入:

异常记录:
- 有时插入数字时会出现不断执行循环的情况,尽管这种错误不完全因为预设执行100次,但还是后面把循环的指令条件该作了m!=4
- m和n的错误输入如果为字母将会带来很大的问题,在上面未修改为m!=4的时候,尚循环100次停止,目前需要执行错误行为完毕。后期还需调整。
目前的main.c为:
#include <iostream>
#include <vector>
#include "bst.h"
#include "VisualTree.h"
int main(int argc, char*argv[])
{
typedef int ValueType;
typedef TreeNode<ValueType> NodeType;
BSTree<ValueType> tree;
VisualTree<NodeType, ValueType> vtree(&NodeType::parent,
&NodeType::left,
&NodeType::right,
&NodeType::val);
int m=0,n=0;
while(m!=4){
printf("-----------------------------------------------\n");
printf("--------------------请输入指令-------------------\n");
printf("--- 插入:1,num 查找:2,num ---\n");
printf("--- 删除:3,num 退出:4 ---\n");
printf("--- (注:num设定为0~100) ---\n");
printf("-----------------------------------------------\n");
scanf("%d,%d",&m,&n);
printf("\n-----------------------------------------------\n");
//健壮性1
if(m!=1&&m!=2&&m!=3&&m!=4){
printf("输入指令错误,请重新输入。\n");
continue;
}
//健壮性2
if(n<0||n>100){
printf("输入数字错误,请重新输入。\n");
continue;
}
if(m==1){
ValueType v =n;
tree.insert(v);
std::cout << "insert : " << v << std::endl;
vtree.draw(tree.root());
}else if (m==2){
ValueType search =n;
if(!tree.find(search)){
printf("未找到\n");
}else{
printf("已找到\n");
}
}else if(m==3){
ValueType search=n;
if(!tree.find(search)){
printf("未找到\n");
}else{
printf("已找到,并删除\n");
}
TreeNode<int> *p=tree.find(search);
tree.remove(p);
vtree.draw(tree.root());
}else if(m==4){
break;
}
}
return 0;
}
可以说,已经完成了阶段三的工作。
六、阶段四:加入调整规则使二叉搜索树变为平衡树
七、阶段五:动态显示二叉平衡树
使用上上篇博客里对二叉搜索树转换为二叉平衡树的思想,时间关系找了一篇别人的博文,代码稍作改动,内容如下:
AVLTree.h
//
// AVLTree.h
// DrawvBinarySearchTree
//
// Created by 张立鹏 on 2018/11/1.
// Copyright © 2018年 张立鹏. All rights reserved.
//
#ifndef AVLTree_h
#define AVLTree_h
#include <iostream>
#include <algorithm>
using namespace std;
#pragma once
//平衡二叉树结点
template <typename T>
struct AvlNode
{
T data;
int height; //结点所在高度,校验平衡度
AvlNode<T> *left;
AvlNode<T> *right;
AvlNode<T>(const T theData) : data(theData), left(NULL), right(NULL), height(0){}
};
static int shuchu[50]={0};
static int s=0;
//AVLTree
template <typename T>
class AvlTree
{
public:
AvlTree<T>(){}
~AvlTree<T>(){}
AvlNode<T> *root;
//插入结点
void Insert(AvlNode<T> *&t, T x);
//删除结点
bool Delete(AvlNode<T> *&t, T x);
//查找是否存在给定值的结点
bool Contains(AvlNode<T> *t, const T x) const;
//中序遍历
void InorderTraversal(AvlNode<T> *t);
//前序遍历
void PreorderTraversal(AvlNode<T> *t);
//最小值结点
AvlNode<T> *FindMin(AvlNode<T> *t) const;
//最大值结点
AvlNode<T> *FindMax(AvlNode<T> *t) const;
private:
//求树的高度
int GetHeight(AvlNode<T> *t);
//单旋转 左
AvlNode<T> *LL(AvlNode<T> *t);
//单旋转 右
AvlNode<T> *RR(AvlNode<T> *t);
//双旋转 右左
AvlNode<T> *LR(AvlNode<T> *t);
//双旋转 左右
AvlNode<T> *RL(AvlNode<T> *t);
};
template <typename T>
AvlNode<T> * AvlTree<T>::FindMax(AvlNode<T> *t) const
{
if (t == NULL)
return NULL;
if (t->right == NULL)
return t;
return FindMax(t->right);
}
template <typename T>
AvlNode<T> * AvlTree<T>::FindMin(AvlNode<T> *t) const
{
if (t == NULL)
return NULL;
if (t->left == NULL)
return t;
return FindMin(t->left);
}
template <typename T>
int AvlTree<T>::GetHeight(AvlNode<T> *t)
{
if (t == NULL)return -1;
else return t->height;
}
//单旋转
//左左插入导致的不平衡
template <typename T>
AvlNode<T> * AvlTree<T>::LL(AvlNode<T> *t)
{
AvlNode<T> *q = t->left;
t->left = q->right;
q->right = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
//单旋转
//右右插入导致的不平衡
template <typename T>
AvlNode<T> * AvlTree<T>::RR(AvlNode<T> *t)
{
AvlNode<T> *q = t->right;
t->right = q->left;
q->left = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
//双旋转
//插入点位于t的左儿子的右子树
template <typename T>
AvlNode<T> * AvlTree<T>::LR(AvlNode<T> *t)
{
//双旋转可以通过两次单旋转实现
//对t的左结点进行RR旋转,再对根节点进行LL旋转
RR(t->left);
return LL(t);
}
//双旋转
//插入点位于t的右儿子的左子树
template <typename T>
AvlNode<T> * AvlTree<T>::RL(AvlNode<T> *t)
{
LL(t->right);
return RR(t);
}
template <typename T>
void AvlTree<T>::Insert(AvlNode<T> *&t, T x)
{
if (t == NULL)
t = new AvlNode<T>(x);
else if (x < t->data)
{
Insert(t->left, x);
//判断平衡情况
if (GetHeight(t->left) - GetHeight(t->right) > 1)
{
//分两种情况 左左或左右
if (x < t->left->data)//左左
t = LL(t);
else //左右
t = LR(t);
}
}
else if (x > t->data)
{
Insert(t->right, x);
if (GetHeight(t->right) - GetHeight(t->left) > 1)
{
if (x > t->right->data)
t = RR(t);
else
t = RL(t);
}
}
else
;//数据重复
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
template <typename T>
bool AvlTree<T>::Delete(AvlNode<T> *&t, T x)
{
//t为空 未找到要删除的结点
if (t == NULL)
return false;
//找到了要删除的结点
else if (t->data == x)
{
//左右子树都非空
if (t->left != NULL && t->right != NULL)
{//在高度更大的那个子树上进行删除操作
//左子树高度大,删除左子树中值最大的结点,将其赋给根结点
if (GetHeight(t->left) > GetHeight(t->right))
{
t->data = FindMax(t->left)->data;
Delete(t->left, t->data);
}
else//右子树高度更大,删除右子树中值最小的结点,将其赋给根结点
{
t->data = FindMin(t->right)->data;
Delete(t->right, t->data);
}
}
else
{//左右子树有一个不为空,直接用需要删除的结点的子结点替换即可
AvlNode<T> *old = t;
t = t->left ? t->left: t->right;//t赋值为不空的子结点
delete old;
}
}
else if (x < t->data)//要删除的结点在左子树上
{
//递归删除左子树上的结点
Delete(t->left, x);
//判断是否仍然满足平衡条件
if (GetHeight(t->right) - GetHeight(t->left) > 1)
{
if (GetHeight(t->right->left) > GetHeight(t->right->right))
{
//RL双旋转
t = RL(t);
}
else
{//RR单旋转
t = RR(t);
}
}
else//满足平衡条件 调整高度信息
{
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
}
else//要删除的结点在右子树上
{
//递归删除右子树结点
Delete(t->right, x);
//判断平衡情况
if (GetHeight(t->left) - GetHeight(t->right) > 1)
{
if (GetHeight(t->left->right) > GetHeight(t->left->left))
{
//LR双旋转
t = LR(t);
}
else
{
//LL单旋转
t = LL(t);
}
}
else//满足平衡性 调整高度
{
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
}
return true;
}
//前序遍历
template <typename T>
void AvlTree<T>::PreorderTraversal(AvlNode<T> *t)
{
if (t)
{
shuchu[s]=t->data;
s++;
PreorderTraversal(t->left);
PreorderTraversal(t->right);
}
}
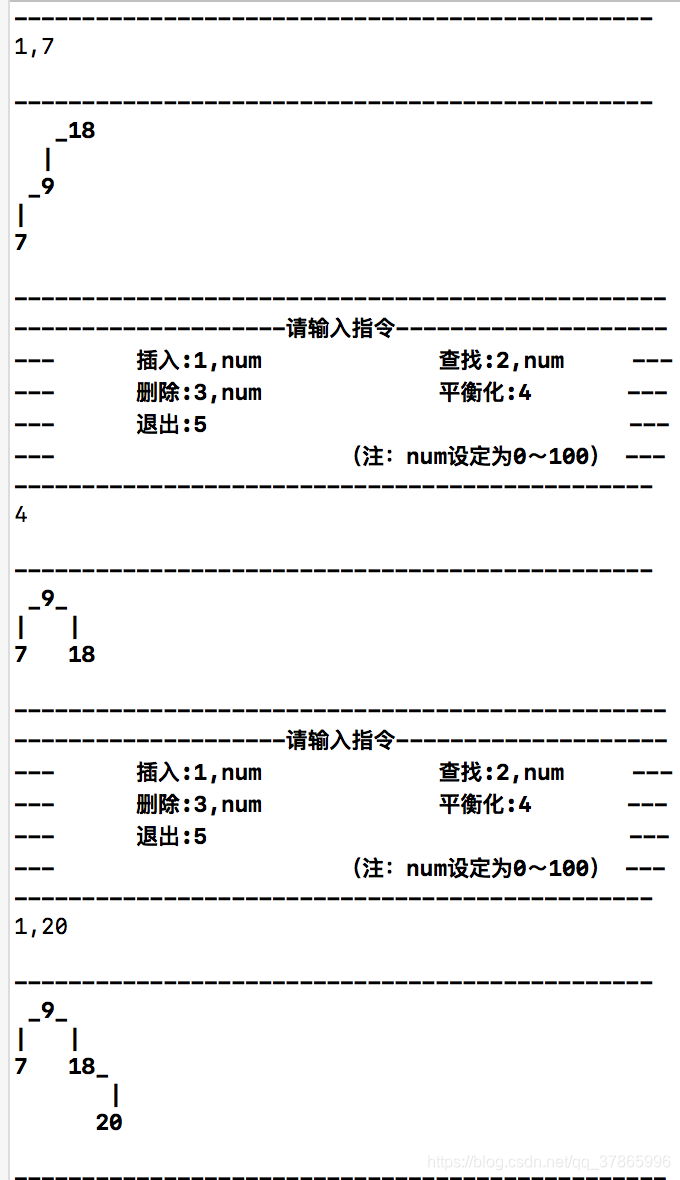
#endif /* AVLTree_h */
运行界面如下:

八、阶段六:使用多种方式显示二叉平衡树
1.java 2D
画板部分参考:https://blog.youkuaiyun.com/qq_40286361/article/details/78014795,这是使用java2D画二叉树的,后面也可以对前面阶段的工作进行拓展和使用。
既然如此,我们先对找到的博客进行研究,代码也放到这边进行参考和学习。
MutableInteger.java 用以传递可变整数,对象是函数返回值
package Btree;
public class MutableInteger {
public int value;
public MutableInteger(int x) { value = x; }
public MutableInteger() { value = 0; }
public boolean equals(int x) {
if ( x==value )
return true;
else
return false;
}
public int getValue() { return value; }
public void setValue(int value) { this.value = value; }
}
Tnode.java
package tree;
import Btree.MutableInteger;
import java.util.LinkedList;
import java.util.List;
public class Tnode {
private String name; //该结点名字
private int layer = 0; //该结点层级
private int x = -1; //x坐标
private List<Tnode> childs = null; //保存该结点的孩子
public Tnode(String name) { this.name = name; }
public Tnode() { this.name = null; }
public void add(Tnode n) {
if (childs==null)
childs = new LinkedList<Tnode>();//这里可以改为ArrayList
n.layer = this.layer + 1;
setChildLayer(n);
childs.add(n);
}
private void setChildLayer(Tnode n) {//递归设置层级,深度优先
if (n.hasChild()) {
List<Tnode> c = n.getChilds();
for (Tnode node : c) {
node.layer = n.layer + 1;
setChildLayer(node);
}
}
}
public void CoordinateProcess(MutableInteger maxX, MutableInteger maxY) { CoordinateProcess(this, maxX, maxY); }
public static void CoordinateProcess(Tnode n, MutableInteger maxX, MutableInteger maxY) {
//max其实是用来布置画布的大小而设置的返回值
//默认的根节点坐标是(0,0),即x=0,layer=0
setx(n, new MutableInteger(0), maxX, maxY);
}
private static void setx(Tnode n, MutableInteger va, MutableInteger maxX, MutableInteger maxY) {//va其实只是用来保存中间结果用来调用的
if (n.hasChild()) {
List<Tnode> c = n.getChilds();
c.get(0).x = va.value;
setx(c.get(0), va, maxX, maxY);
for (int i=1; i<c.size(); i++) {
setx(c.get(i), va, maxX, maxY);
}
n.x = c.get(0).x;//本结点的x是第一个孩子的x
} else {
n.x = va.value++;
}
//保存最大的x,y返回
if (n.getX()>maxX.value) {
maxX.value = n.getX();
}
if (n.getLayer()>maxY.value) {
maxY.value = n.getLayer();
}
}
public String getName() { return name; }
public void setName(String name) { this.name = name; }
public int getLayer() { return layer; }
public int getX() { return x; }
public void setLayer(int layer) { this.layer = layer; }
public List<Tnode> getChilds() { return childs; }
public void setChilds(List<Tnode> childs) { this.childs = childs; }
public boolean hasChild() { return childs==null ? false : true; }
public void printAllNode(Tnode n) {//递归打印所有结点,深优
System.out.println(n.toString());
if (n.hasChild()) {
List<Tnode> c = n.getChilds();
for (Tnode node : c) {
printAllNode(node);
}
}
}
public void printAllNode() { printAllNode(this); }
public String getAllNodeName(Tnode n) {
String s = n.toString()+"/n";
if (n.hasChild()) {
List<Tnode> c = n.getChilds();
for (Tnode node : c) {
s += getAllNodeName(node)+"/n";
}
}
return s;
}
public String getAllNodeName() { return getAllNodeName(this); }
public String toString() { return name; }
}TreePanel.java
package Btree;
import java.awt.*;
import java.util.List;
import javax.swing.JPanel;
public class TreePanel extends JPanel {
private static final long serialVersionUID = 1L;
private Tnode tree; //保存整棵树
private int gridWidth = 170; //每个结点的宽度
private int gridHeight = 20; //每个结点的高度
private int vGap = 50; //每2个结点的垂直距离
private int hGap = 30; //每2个结点的水平距离
private int startY = 10; //根结点的Y,默认距离顶部10像素
private int startX = 10; //根结点的X,默认距离左端10像素
//改进之后的程序呢就不是原文的对对齐方式啦,所以下面几行是没用的
//private int childAlign; //孩子对齐方式
//public static int CHILD_ALIGN_ABSOLUTE = 0; //相对Panel居中
//public static int CHILD_ALIGN_RELATIVE = 1; //相对父结点居中
private Font font = new Font("微软雅黑",Font.BOLD,14); //描述结点的字体
private Color gridColor = Color.BLACK; //结点背景颜色
private Color linkLineColor = Color.BLACK; //结点连线颜色
private Color stringColor = Color.WHITE; //结点描述文字的颜色
/*放弃了原文的内容,这是由于我们只有一种画法,而不是中间对其或是左对齐等
public TreePanel() { this(null,CHILD_ALIGN_ABSOLUTE); }
public TreePanel(Tnode n) { this(n,CHILD_ALIGN_ABSOLUTE); }
public TreePanel(int childAlign) { this(null,childAlign); }
public TreePanel(Tnode n, int childAlign) {
super();
setTree(n);
this.childAlign = childAlign;
}
*/
public TreePanel() { this(null); }
public TreePanel(Tnode n) {
super();
setTree(n);
}
public void setTree(Tnode n) { tree = n; }
//重写,调用自己的绘制方法
public void paintComponent(Graphics g) {
//startX = (getWidth()-gridWidth)/2;//这是居中方式的设置,放弃原文方法
super.paintComponent(g);
g.setFont(font);
drawAllNode(tree, g);
}
/**
* 递归绘制整棵树
* n 被绘制的Node
* xPos 根节点的绘制X位置
* g 绘图上下文环境
*/
public void drawAllNode(Tnode n, Graphics g) {
int y = n.getLayer()*(vGap+gridHeight)+startY;
int x = n.getX()*(hGap+gridWidth)+startX;
int fontY = y + gridHeight - 5; //5为测试得出的值,你可以通过FM计算更精确的,但会影响速度
g.setColor(gridColor);
g.fillRoundRect(x, y, gridWidth, gridHeight, 10, 10); //画结点的格子
g.setColor(stringColor);
g.drawString(n.toString(), x+5, fontY); //画结点的名字
if (n.hasChild()) {
g.setColor(linkLineColor);
g.drawLine(x+gridWidth/2, y+gridHeight, x+gridWidth/2, y+gridHeight+vGap/2);
List<Tnode> c = n.getChilds();
int i = 0;
for (Tnode node : c) {
int newX = node.getX()*(hGap+gridWidth)+startX; //孩子结点起始X
g.setColor(linkLineColor);
g.drawLine(newX+gridWidth/2, y+gridHeight+vGap/2, newX+gridWidth/2, y+gridHeight+vGap);
drawAllNode(node, g);
i++;
if (i==c.size()) {
g.setColor(linkLineColor);
g.drawLine(x+gridWidth/2, y+gridHeight+vGap/2, newX+gridWidth/2, y+gridHeight+vGap/2);
}
}
}
}
public Color getGridColor() { return gridColor; }
public void setGridColor(Color gridColor) { this.gridColor = gridColor; }
public Color getLinkLineColor() { return linkLineColor; }
public void setLinkLineColor(Color gridLinkLine) { this.linkLineColor = gridLinkLine; }
public Color getStringColor() { return stringColor; }
public void setStringColor(Color stringColor) { this.stringColor = stringColor; }
public int getStartY() { return startY; }
public void setStartY(int startY) { this.startY = startY; }
public int getStartX() { return startX; }
public void setStartX(int startX) { this.startX = startX; }
public int getGridWidth() { return gridWidth; }
public void setGridWidth(int gridWidth) { this.gridWidth = gridWidth; }
public int getGridHight() { return gridHeight; }
public void setGridHeight(int gridHeight) { this.gridHeight = gridHeight; }
public int getVGap() { return vGap; }
public void setVGap(int vGap) { this.vGap = vGap; }
public int getHGap() { return hGap; }
public void setHGap(int hGap) { this.hGap = hGap; }
}原博主的实现效果如下:

可见是可以实现的。
目前我要做两件事情:
1.使用Java实现同样的二叉树输出;
2.使用画板实现二叉树的输出。
因为画板是在使用Java窗体的基础上定义各种画面元素的位置,而位置的判断常常伴随着裂点等操作,因此是画板代码和B-tree的结合。
首先我找来了graph2D打印二叉树的代码(看来我有时间得把前面的工作拓展一下咯),并作以研究,经本人改动之后如下:
TreeNode.java
package gg;
public class TreeNode {
String data;
TreeNode left;
TreeNode right;
int layerNo, x;
/*三个构造函数*/
public TreeNode(String v) {
data = v;
left = null;
right = null;
}
public TreeNode(String v, TreeNode l, TreeNode r) {
data = v;
left = l;
right = r;
}
public TreeNode() {
// 默认构造函数
}
}
Mytree.java
package gg;
import gg.TreeNode;
public class Mytree {
public int cx, cy;
public int i = 0, j = 0;
TreeNode root; //根节点
int maxDepth; //最大深度
Mytree(String v) { //构造函数
insert(v); //自定义insert函数
}
void insert(String v) {
TreeNode p = new TreeNode(), head; //TreeNode
TreeNode st[];
st = new TreeNode[v.length() + 10];
int top = -1, k = 0, j = 0; //j为String v中字母的索引位置
char ch;
head = root; // 建立的二叉树初始时为空
ch = v.charAt(j);//harAt(int index)方法是一个能够用来检索特定索引下的字符的String实例的方法.charAt()方法返回指定索引位置的char值。索引范围为0~length()-1
if (head == null) { // 头结点相当于一个虚拟的头ROOT.
head = new TreeNode(""+ch);
j++;
ch = v.charAt(j);
}
int i = v.length();
while (j < v.length() - 1) // str未扫描完时循环
{
switch (ch) {
case '(':
top++;
k = 1;
break;
case ')':
head = st[top - k];
top -= k;
k = 1;
break;
case ',':
head = st[top];
top++;
k = 2;
break; // 上述选择一个变量来确定有几个节点
default:
p = new TreeNode("" + ch);
// 已建立二叉树根结点
{
switch (k) {
case 1:
head.left = p;
st[top] = head;
head = head.left;
break;
case 2:
head.right = p;
st[top] = head;
head = head.right;// 插入,并且保存一个数组中
break;
}
}
}
j++;
ch = v.charAt(j);
}
root = st[0];
}
public void calcX(TreeNode tn, int x) {
tn.x = x;
if (tn.left != null)
calcX(tn.left, x - 1);
if (tn.right != null)
calcX(tn.right, x + 1);
}
public void calcX2(TreeNode tn, int x) {
tn.x = x;
int dx = (int) Math.pow(2, maxDepth - tn.layerNo - 1);
if (tn.left != null)
calcX2(tn.left, x - dx);
if (tn.right != null)
calcX2(tn.right, x + dx);
}
// 计算每个结点的x坐标,采用前序遍历
// *******************************************************************
public void calcDepth(TreeNode tn, int d) {
tn.layerNo = d;
if (maxDepth < d)
maxDepth = d;
d += 1;
if (tn.left != null)
calcDepth(tn.left, d);
if (tn.right != null)
calcDepth(tn.right, d);
}
// 计算每个结点的层号及树的最大深度,采用前序遍历
// *************************************************************************
public void printLayer() {
calcDepth(root, 1); // 先计算出每个结点的层号及树的最大深度maxDepth
calcX2(root, (int) Math.pow(2, maxDepth - 1));
}
}study.java
package gg;
import java.awt.Color;
import java.awt.Event;
import java.awt.Frame;
import java.awt.Graphics;
import java.awt.Image;
import java.awt.Toolkit;
import gg.TreeNode;
import gg.Mytree;
public class study extends Frame {
String temp = " ";// 下面交换字符串有用。
static String tree = "a(b(l,m),e(f(h,j),i(k,g)))";//自定义二叉树
Toolkit toolkit = Toolkit.getDefaultToolkit();
public static void main(String args[]) {
Frame f = new study();
f.setTitle("二叉树的图形展示 ———WittPeng");
f.setBackground(Color.LIGHT_GRAY);
f.setBounds(1000, 500, 1000, 800);//x,y,width,height
f.setVisible(true); //窗体可视
f.setResizable(false);
}
// 类似于数据结构中的链表
public boolean handleEvent(Event evt) {
if (evt.id == Event.WINDOW_DESTROY)
System.exit(0);
return super.handleEvent(evt);
}
public void paint(Graphics g) {
int i = 0, j = 0;
Mytree bt = new Mytree(tree);
TreeNode Node, tNode[];
int cx[], cy[];
Node = bt.root;
bt.printLayer();// 首先遍历一下,得到坐标初始化。
int top = -1;
tNode = new TreeNode[bt.maxDepth];// 为了下层遍历出坐标定义的一个数组
cx = new int[tree.length() + 1];
cy = new int[tree.length() + 1];
cx[0] = 1;
cy[0] = 1;
if (bt.root != null) {
top++;
tNode[top] = bt.root;
while (top > -1) {
Node = tNode[top];
top--;
g.setColor(Color.PINK);//节点背景颜色
g.fillOval(100 + Node.x * 40, Node.layerNo * 50, 40, 20);//x,y,width,height
g.setColor(Color.BLACK);//节点字体颜色
g.drawString(Node.data, 120 + Node.x * 40,
Node.layerNo * 50 + 13);//String Str,x,y
cx[i] = 120 + Node.x * 40;
cy[i] = Node.layerNo * 50;// cx cy 两坐标统计节点的坐标值,相同下标对应的XY坐标为节点坐标。
i++;
if (Node.right != null) {
top++;
tNode[top] = Node.right;
}
if (Node.left != null) {
top++;
tNode[top] = Node.left;
}
}
}
// 非递归遍历出树的结点
g.setColor(Color.black);//线条颜色
top = 0;
int k = 1, s = 0, a = 0, b = i;
s = cx[1] - cx[0];
int tempx[], tx[];
tx = new int[25];
tx[0] = cx[0];
for (i = 0; i < bt.maxDepth - 1; i++) {
tempx = new int[25];// 定义了两个数组保存坐标,
for (j = i; j < b; j++) {// j是结点的个数
if (cy[i + 1] == cy[j]) {// 如果层数相等就存入其坐标,堆栈原理解决关系问题,先把每层的都遍历一遍,同层中存在栈中
tempx[top] = cx[j];
if (tempx[top] != 0) {
top++;
}
}
}
if (cy[i + 2] - cy[i + 1] != 50) {
cy[i + 2] = (i + 3) * 50;
cx[i + 2] = 0;
}
a = top;// a统计本层有几个节点,便于下面画线变化父节点。
if (top != 0) {
for (; top >= 0; top--) {
for (int c = 0; c <= k; c++) {
if (tempx[top] + s == tx[c])
g.drawLine(tx[c], cy[i] + 20, tempx[top], cy[i + 1]);
if (tempx[top] - s == tx[c])
g.drawLine(tx[c], cy[i] + 20, tempx[top], cy[i + 1]);
}
if ((a - top) % 2 == 1) {
k--;
}
}
}
s = s / 2;// S作为两节点的间隔数,
tx = new int[25];// 上一层结点的记录
k = a;// 将下一层结点的个数赋值给K
tx = tempx;// 结点坐标保持
top = 0;// 初始化栈
tempx = new int[25];// 下一层结点的保存点
}
String com = "Fight for Dream,WittPeng!, 18-11-3";
g.drawString(com, 840, 700);
}
}
效果如下:
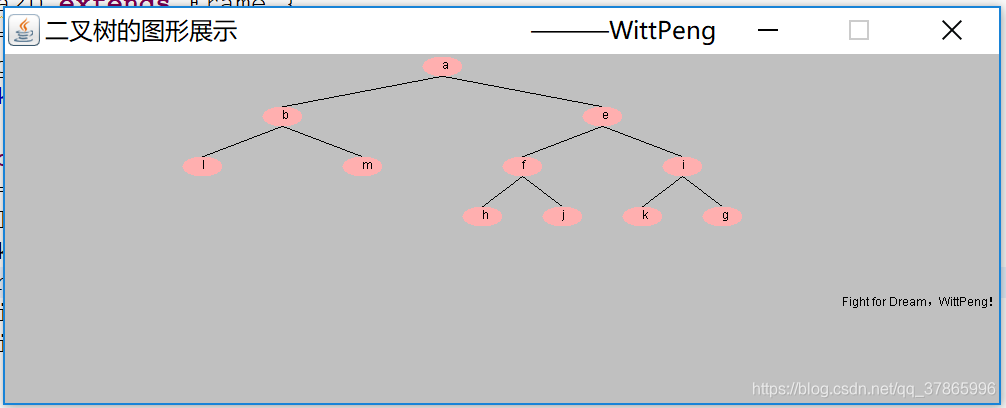
时间紧迫,加入二叉搜索树代码后,仅在平衡树得到后进行展示,其实还是两个东西,只是相互调用了一下。有时间还是要把它们融为一体比较好。
找得一代码AVLTree.java
package gj;
import java.sql.Connection;
import java.sql.DriverManager;
import java.sql.ResultSet;
import java.sql.SQLException;
import java.sql.Statement;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Scanner;
import java.util.Stack;
import java.util.Iterator;
import java.util.NoSuchElementException;
import java.util.Queue;
import gj.Sb;
import gj.Java2D;
public class AVLTree<E> {
public static String[] a=new String[30];
public static String[] b=new String[30];
public static String newStr=new String();
public static StringBuffer sb=new StringBuffer();
Entry<E> root = null;//根节点
private int size = 0;//树中元素个数
public AVLTree(){
}
public int size(){
return size;
}
/**
* @param p 最小旋转子树的根节点
* 向左旋转之后p移到p的左子树处,p的右子树B变为此最小子树根节点,
* B的左子树变为p的右子树
* 比如: A(-2) B(1)
* \ 左旋转 / \
* B(0) ----> A(0) \
* / \ \ \
* BL(0) BR(0) BL(0) BR(0)
* 旋转之后树的深度之差不超过1
*/
private void rotateLeft(Entry<E> p) {
if(p!=null){
Entry<E> r = p.right;
p.right = r.left; //把p右子树的左节点嫁接到p的右节点,如上图,把BL作为A的右子节点
if (r.left != null) //如果B的左节点BL不为空,把BL的父节点设为A
r.left.parent = p;
r.parent = p.parent; //A的父节点设为B的父节点
if (p.parent == null) //如果p是根节点
root = r; //r变为父节点,即B为父节点
else if (p.parent.left == p) //如果p是左子节点
p.parent.left = r; //p的父节点的左子树为r
else //如果p是右子节点
p.parent.right = r; //p的父节点的右子树为r
r.left = p; //p变为r的左子树,即A为B的左子树
p.parent = r; //同时更改p的父节点为r,即A的父节点为B
}
}
/**
* @param p 最小旋转子树的根节点
* 向右旋转之后,p移到p的右子节点处,p的左子树B变为最小旋转子树的根节点
* B的右子节点变为p的左节点、
* 例如: A(2) B(-1)
* / 右旋转 / \
* B(0) ------> / A(0)
* / \ / /
* BL(0) BR(0) BL(0) BR(0)
*/
private void rotateRight(Entry<E> p){
System.out.println("绕"+p.element+"右旋");
if(p!=null){
Entry<E> l = p.left;
p.left = l.right; //把B的右节点BR作为A的左节点
if (l.right != null) //如果BR不为null,设置BR的父节点为A
l.right.parent = p;
l.parent = p.parent; //A的父节点赋给B的父节点
if (p.parent == null) //如果p是根节点
root = l; //B为根节点
else if (p.parent.right == p) //如果A是其父节点的左子节点
p.parent.right = l; //B为A的父节点的左子树
else //如果A是其父节点的右子节点
p.parent.left = l; //B为A的父节点的右子树
l.right = p; //A为B的右子树
p.parent = l; //设置A的父节点为B
}
}
/**
* 平衡而二叉树的插入操作
* 基本原理为:
* 1.首先如同二叉排序树一般,找到其要插入的节点的位置,并把元素插入其中;
* 2.自下向上进行回溯,回溯做两个事情:
* (1)其一是修改祖先节点的平衡因子,当插入 一个节点时只有根节点到插入节点
* 的路径中的节点的平衡因子会被改变,而且改变的原则是当插入节点在某节点(称为A)
* 的左子树 中时,A的平衡因子(称为BF)为BF+1,当插入节点在A的右子树中时A的BF-1,
* 而判断插入节点在左子树中还是右子树中只要简单的比较它与A的大小
* (2)在改变祖先节点的平衡因子的同时,找到最近一个平衡因子大于2或小于-2的节点,
* 从这个节点开始调整最小不平衡树进行旋转调整,关于如何调整见下文。
* 由于调整后,最小不平衡子树的高度与插入节点前的高度相同,故不需继续要调整祖先节点。
* 这里还有一个特殊情况,如果调整BF时,发现某个节点的BF变为0了,则停止向上继续调整,
* 因为这表明此节点中高度小的子树增加了新节点,高度不变,那么祖先节点的BF自然不变。
*
*
*/
public boolean add(E element){
Entry<E> t = root;
if(t == null){
root = new Entry<E>(element,null);
size = 1;
return true;
}
int cmp;
Entry<E> parent; //保存t的父节点
Comparable<? super E> e = (Comparable<? super E>) element;
//从根节点向下搜索,找到插入位置
do {
parent = t;
cmp = e.compareTo(t.element);
if(cmp < 0){
t = t.left;
}else if(cmp > 0){
t = t.right;
}else{
return false;
}
} while (t!=null);
Entry<E> child = new Entry(element,parent);
if(cmp < 0){
parent.left = child;
}else{
parent.right = child;
}
//自下向上回溯,查找最近不平衡节点
while(parent!=null){
cmp = e.compareTo(parent.element);
if(cmp < 0){ //插入节点在parent的左子树中
parent.balance++;
}else{ //插入节点在parent的右子树中
parent.balance--;
}
if(parent.balance == 0){ //此节点的balance为0,不再向上调整BF值,且不需要旋转
break;
}
if(Math.abs(parent.balance) == 2){ //找到最小不平衡子树根节点
fixAfterInsertion(parent);
break; //不用继续向上回溯
}
parent = parent.parent;
}
size ++;
return true;
}
/**
* 调整的方法:
* 1.当最小不平衡子树的根(以下简称R)为2时,即左子树高于右子树:
* 如果R的左子树的根节点的BF为1时,做右旋;
* 如果R的左子树的根节点的BF为-1时,先左旋然后再右旋
*
* 2.R为-2时,即右子树高于左子树:
* 如果R的右子树的根节点的BF为1时,先右旋后左旋
* 如果R的右子树的根节点的BF为-1时,做左旋
*
* 至于调整之后,各节点的BF变化见代码
*/
private void fixAfterInsertion(Entry<E> p){
if(p.balance == 2){
leftBalance(p);
}
if(p.balance == -2){
rightBalance(p);
}
}
/**
* 做左平衡处理
* 平衡因子的调整如图:
* t rd
* / \ / \
* l tr 左旋后右旋 l t
* / \ -------> / \ / \
* ll rd ll rdl rdr tr
* / \
* rdl rdr
*
* 情况2(rd的BF为0)
*
*
* t rd
* / \ / \
* l tr 左旋后右旋 l t
* / \ -------> / \ \
* ll rd ll rdl tr
* /
* rdl
*
* 情况1(rd的BF为1)
*
*
* t rd
* / \ / \
* l tr 左旋后右旋 l t
* / \ -------> / / \
* ll rd ll rdr tr
* \
* rdr
*
* 情况3(rd的BF为-1)
*
*
* t l
* / 右旋处理 / \
* l ------> ll t
* / \ /
* ll rd rd
* 情况4(L等高)
*/
private boolean leftBalance(Entry<E> t){
boolean heightLower = true;
Entry<E> l = t.left;
switch (l.balance) {
case LH: //左高,右旋调整,旋转后树的高度减小
t.balance = l.balance = EH;
rotateRight(t);
break;
case RH: //右高,分情况调整
Entry<E> rd = l.right;
switch (rd.balance) { //调整各个节点的BF
case LH: //情况1
t.balance = RH;
l.balance = EH;
break;
case EH: //情况2
t.balance = l.balance = EH;
break;
case RH: //情况3
t.balance = EH;
l.balance = LH;
break;
}
rd.balance = EH;
rotateLeft(t.left);
rotateRight(t);
break;
case EH: //特殊情况4,这种情况在添加时不可能出现,只在移除时可能出现,旋转之后整体树高不变
l.balance = RH;
t.balance = LH;
rotateRight(t);
heightLower = false;
break;
}
return heightLower;
}
/**
* 做右平衡处理
* 平衡因子的调整如图:
* t ld
* / \ / \
* tl r 先右旋再左旋 t r
* / \ --------> / \ / \
* ld rr tl ldl ldr rr
* / \
* ldl ldr
* 情况2(ld的BF为0)
*
* t ld
* / \ / \
* tl r 先右旋再左旋 t r
* / \ --------> / \ \
* ld rr tl ldl rr
* /
* ldl
* 情况1(ld的BF为1)
*
* t ld
* / \ / \
* tl r 先右旋再左旋 t r
* / \ --------> / / \
* ld rr tl ldr rr
* \
* ldr
* 情况3(ld的BF为-1)
*
* t r
* \ 左旋 / \
* r -------> t rr
* / \ \
* ld rr ld
* 情况4(r的BF为0)
*/
private boolean rightBalance(Entry<E> t){
boolean heightLower = true;
Entry<E> r = t.right;
switch (r.balance) {
case LH: //左高,分情况调整
Entry<E> ld = r.left;
switch (ld.balance) { //调整各个节点的BF
case LH: //情况1
t.balance = EH;
r.balance = RH;
break;
case EH: //情况2
t.balance = r.balance = EH;
break;
case RH: //情况3
t.balance = LH;
r.balance = EH;
break;
}
ld.balance = EH;
rotateRight(t.right);
rotateLeft(t);
break;
case RH: //右高,左旋调整
t.balance = r.balance = EH;
rotateLeft(t);
break;
case EH: //特殊情况4
r.balance = LH;
t.balance = RH;
rotateLeft(t);
heightLower = false;
break;
}
return heightLower;
}
/**
* 查找指定元素,如果找到返回其Entry对象,否则返回null
*/
private Entry<E> getEntry(Object element) {
Entry<E> tmp = root;
Comparable<? super E> e = (Comparable<? super E>) element;
int c;
while (tmp != null) {
c = e.compareTo(tmp.element);
if (c == 0) {
return tmp;
} else if (c < 0) {
tmp = tmp.left;
} else {
tmp = tmp.right;
}
}
return null;
}
/**
* 平衡二叉树的移除元素操作
*
*/
public boolean remove(Object o){
Entry<E> e = getEntry(o);
if(e!=null){
deleteEntry(e);
return true;
}
return false;
}
private void deleteEntry(Entry<E> p){
size --;
//如果p左右子树都不为空,找到其直接后继,替换p,之后p指向s,删除p其实是删除s
//所有的删除左右子树不为空的节点都可以调整为删除左右子树有其一不为空,或都为空的情况。
if (p.left != null && p.right != null) {
Entry<E> s = successor(p);
p.element = s.element;
p = s;
}
Entry<E> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) { //如果其左右子树有其一不为空
replacement.parent = p.parent;
if (p.parent == null) //如果p为root节点
root = replacement;
else if (p == p.parent.left) //如果p是左孩子
p.parent.left = replacement;
else //如果p是右孩子
p.parent.right = replacement;
p.left = p.right = p.parent = null; //p的指针清空
//这里更改了replacement的父节点,所以可以直接从它开始向上回溯
fixAfterDeletion(replacement);
} else if (p.parent == null) { // 如果全树只有一个节点
root = null;
} else { //左右子树都为空
fixAfterDeletion(p); //这里从p开始回溯
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
/**
* 返回以中序遍历方式遍历树时,t的直接后继
*/
static <E> Entry<E> successor(Entry<E> t) {
if (t == null)
return null;
else if (t.right != null) { //往右,然后向左直到尽头
Entry<E> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { //right为空,如果t是p的左子树,则p为t的直接后继
Entry<E> p = t.parent;
Entry<E> ch = t;
while (p != null && ch == p.right) { //如果t是p的右子树,则继续向上搜索其直接后继
ch = p;
p = p.parent;
}
return p;
}
}
/**
* 删除某节点p后的调整方法:
* 1.从p开始向上回溯,修改祖先的BF值,这里只要调整从p的父节点到根节点的BF值,
* 调整原则为,当p位于某祖先节点(简称A)的左子树中时,A的BF减1,当p位于A的
* 右子树中时A的BF加1。当某个祖先节点BF变为1或-1时停止回溯,这里与插入是相反的,
* 因为原本这个节点是平衡的,删除它的子树的某个节点并不会改变它的高度
*
* 2.检查每个节点的BF值,如果为2或-2需要进行旋转调整,调整方法如下文,
* 如果调整之后这个最小子树的高度降低了,那么必须继续从这个最小子树的根节点(假设为B)继续
* 向上回溯,这里和插入不一样,因为B的父节点的平衡性因为其子树B的高度的改变而发生了改变,
* 那么就可能需要调整,所以删除可能进行多次的调整。
*
*/
private void fixAfterDeletion(Entry<E> p){
boolean heightLower = true; //看最小子树调整后,它的高度是否发生变化,如果减小,继续回溯
Entry<E> t = p.parent;
Comparable<? super E> e = (Comparable<? super E>)p.element;
int cmp;
//自下向上回溯,查找不平衡的节点进行调整
while(t!=null && heightLower){
cmp = e.compareTo(t.element);
/**
* 删除的节点是右子树,等于的话,必然是删除的某个节点的左右子树不为空的情况
* 例如: 10
* / \
* 5 15
* / \
* 3 6
* 这里删除5,是把6的值赋给5,然后删除6,这里6是p,p的父节点的值也是6。
* 而这也是右子树的一种
*/
if(cmp >= 0 ){
t.balance ++;
}else{
t.balance --;
}
if(Math.abs(t.balance) == 1){ //父节点经过调整平衡因子后,如果为1或-1,说明调整之前是0,停止回溯。
break;
}
Entry<E> r = t;
//这里的调整跟插入一样
if(t.balance == 2){
heightLower = leftBalance(r);
}else if(t.balance==-2){
heightLower = rightBalance(r);
}
t = t.parent;
}
}
private static final int LH = 1; //左高
private static final int EH = 0; //等高
private static final int RH = -1; //右高
/**
* 树节点,为方便起见不写get,Set方法
*/
static class Entry<E>{
E element;
Entry<E> parent;
Entry<E> left;
Entry<E> right;
int balance = EH; //平衡因子,只能为1或0或-1
public Entry(E element,Entry<E> parent){
this.element = element;
this.parent = parent;
}
public Entry(){}
@Override
public String toString() {
return element+" BF="+balance;
}
}
public static void BFSOrder(Entry t)
{
if(t==null) return ;
Queue<Entry> queue = new ArrayDeque<Entry>();
//队列小知识:使用offer和poll优于add和remove之处在于它们返回值可以判断成功与否,而不抛出异常
queue.offer(t); //进入队列
int ii=0;
while(!queue.isEmpty())
{
t=queue.poll(); //当前节点出队列
System.out.print(t.element);
a[ii]=t.element.toString();
ii++;
if(t.left!=null) //当前节点左孩子去排队,在前面哦
queue.offer(t.left);
if(t.right!=null) //右孩子排第二
queue.offer(t.right);
}
}
//返回中序遍历此树的迭代器,返回的是一个有序列表
private class BinarySortIterator implements Iterator<E>{
Entry<E> next;
Entry<E> lastReturned;
public BinarySortIterator(){
Entry<E> s = root;
if(s !=null){
while(s.left != null){ //找到中序遍历的第一个元素
s = s.left;
}
}
next = s; //赋给next
}
@Override
public boolean hasNext() {
return next!=null;
}
@Override
public E next() {
Entry<E> e = next;
if (e == null)
throw new NoSuchElementException();
next = successor(e);
lastReturned = e;
return e.element;
}
@Override
public void remove() {
if (lastReturned == null)
throw new IllegalStateException();
// deleted entries are replaced by their successors
if (lastReturned.left != null && lastReturned.right != null)
next = lastReturned;
deleteEntry(lastReturned);
lastReturned = null;
}
}
public Iterator<E> itrator(){
return new BinarySortIterator();
}
private int treeHeight(Entry<E> p){
if(p == null){
return -1;
}
return 1 + Math.max(treeHeight(p.left), treeHeight(p.right));
}
//测试,你也可以任意测试
public static void main(String[] args) {
AVLTree<Integer> tree = new AVLTree<Integer>();
System.out.println("--请输入插入个数---");
Scanner s2=new Scanner(System.in);
int m=s2.nextInt();
System.out.println("------添加------");
int w=1;
while(m!=0)
{
if(w==0){break;}
Scanner s1=new Scanner(System.in);
w=s1.nextInt();
tree.add(w);
m--;
};
// System.out.println("------删除------");
// tree.remove(50);
// tree.remove(66);
//
System.out.println();
tree.BFSOrder(tree.root);
b[0]=a[0];
b[1]="(";
b[2]=a[1];
b[3]="(";
b[4]=a[3];
b[5]=",";
b[6]=a[4];
b[7]=")";
b[8]=",";
b[9]=a[2];
b[10]="(";
b[11]=a[5];
b[12]=",";
b[13]=a[6];
b[14]=")";
b[15]=")";
for(int i=0;i<b.length;i++){
if(b[i]==null)break;
sb.append(b[i]);
}
newStr=sb.toString();
System.out.println("\n"+newStr);
// Iterator<Integer> it = tree.itrator();
// while(it.hasNext()){
// System.out.print(it.next()+" ");
//
// }
}
}
输出:
--请输入插入个数---
7
------添加------
1
2
3
4
5
6
7
4261357
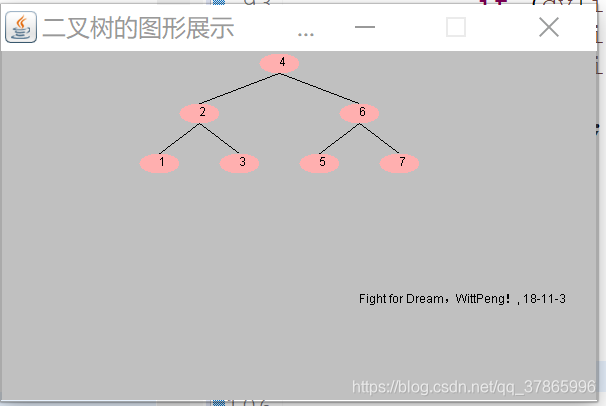
4(2(1,3),6(5,7))
通过值传递可为java2d代码使用,建议使用一下窗体,把上面的代码封装一下,不然会出现很多问题。我的话,以后再写这边的。
2.调用graphviz绘制。
首先找到了《C调用graphviz绘制堆》,首先实现一下这个。
Mac环境下graphviz的安装需要登入 http://www.graphviz.org/,下载对应文件。
可直接安装brew:在终端输入指令
ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"接着
brew install graphviz查看是否安装成功:
dot -v结合VIM可分别实现输入和输出
在这里使用C语言代码生成dot文件,再调用graphziv生成图片。
c语言代码:
#include<stdio.h>
#include<stdlib.h>
struct TreeNode;
typedef struct TreeNode *PtrSearchTree;
typedef PtrSearchTree SearchTree;
struct TreeNode
{
int value;
PtrSearchTree left;
PtrSearchTree right;
};
SearchTree create();
void insert(SearchTree* tree, int value);
void write2dot(SearchTree tree, FILE* fw);
void visualization(SearchTree tree, char* filename);
SearchTree find_min(SearchTree tree);
SearchTree find_max(SearchTree tree);
SearchTree find_iteration(SearchTree tree, int value);
SearchTree find_recursion(SearchTree tree, int value);
SearchTree delete(SearchTree tree, int value);
int main(int argc, char** argv)
{
SearchTree s_tree_1 = create();
visualization(s_tree_1, "searchtree.dot");
PtrSearchTree min = find_min(s_tree_1);
PtrSearchTree max = find_max(s_tree_1);
printf("the min and max is %d, %d, respectively\n", min->value, max->value);
int search = 83;
PtrSearchTree find_result_1 = find_iteration(s_tree_1, search);
PtrSearchTree find_result_2 = find_iteration(s_tree_1, search);
if( find_result_1 && find_result_2 )
printf("search for %d, and the result from iteration and recursion is: %d, %d\n", search, find_result_1->value, find_result_2->value);
s_tree_1 = delete(s_tree_1, 83);
visualization(s_tree_1, "searchtree_afterdelete.dot");
return 0;
}
SearchTree create()
{
SearchTree tree = NULL;
printf("Create Binary Search Tree\nplease enter the element, seperated by space, and stop input by Enter:\n");
int key;
while(1)
{
scanf("%d", &key);
insert(&tree, key);
if( getchar() == '\n' )
break;
}
return tree;
}
void insert(SearchTree* tree, int value)
{
if( *tree == NULL )
{
if( ! ((*tree) = (PtrSearchTree)malloc(sizeof(struct TreeNode))) )
{
printf("insert malloc error\n");
exit(0);
}
(*tree)->value = value;
(*tree)->left = (*tree)->right = NULL;
}
else
{
if( value < (*tree)->value )
insert(&((*tree)->left), value);
else
insert(&((*tree)->right), value);
}
}
void visualization(SearchTree tree, char* filename)
{
FILE *fw;
if( NULL == (fw = fopen(filename, "w")) )
{
printf("open file error");
exit(0);
}
fprintf(fw, "digraph\n{\nnode [shape = Mrecord, style = filled, color = black, fontcolor = white];\n");
write2dot(tree, fw);
fprintf(fw, "}");
fclose(fw);
}
void write2dot(SearchTree tree, FILE* fw)
{
if(tree == NULL)
return ;
else
{
fprintf(fw, "%d [label = \"<f0> | <f1> %d | <f2> \", color = black, fontcolor = white, style = filled];\n", tree->value, tree->value);
}
if(tree->left)
{
fprintf(fw, "%d [label = \"<f0> | <f1> %d | <f2> \", color = black, fontcolor = white, style = filled];\n", tree->left->value, tree->left->value);
fprintf(fw, "%d:f0:sw -> %d:f1;\n", tree->value, tree->left->value);
}
if(tree->right)
{
fprintf(fw, "%d [label = \"<f0> | <f1> %d | <f2> \", color = black, fontcolor = white, style = filled];\n", tree->right->value, tree->right->value);
fprintf(fw, "%d:f2:se -> %d:f1;\n", tree->value, tree->right->value);
}
write2dot(tree->left, fw);
write2dot(tree->right, fw);
}
SearchTree find_min(SearchTree tree)
{
if( !tree )
return NULL;
else
if( !(tree->left) ) return tree;
else
find_min(tree->left);
}
SearchTree find_max(SearchTree tree)
{
if( !tree )
return NULL;
else
if( !(tree->right) ) return tree;
else find_max(tree->right);
}
SearchTree find_recursion(SearchTree tree, int value)
{
if( !tree )
{
printf("have no element(find): %d\n", value);
return NULL;
}
if( value < tree->value )
find_recursion(tree->left, value);
else if( value > tree->value )
find_recursion(tree->right, value);
else
return tree;
}
SearchTree find_iteration(SearchTree tree, int value)
{
while(tree)
{
if( value < tree->value )
tree = tree->left;
else if( value > tree->value )
tree = tree->right;
else
return tree;
}
printf("have no element(find): %d\n", value);
return NULL;
}
SearchTree delete(SearchTree tree, int value)
{
PtrSearchTree temp = NULL;
if( !tree )
{
printf("have no element(delete): %d\n", value);
return NULL;
}
else if( value < tree->value )
tree->left = delete(tree->left, value);
else if( value > tree->value )
tree->right = delete(tree->right, value);
else
{
if( tree->left && tree->right )
{
temp = find_min(tree->right);
tree->value = temp->value;
tree->right = delete(tree->right, temp->value);
}
else
{
temp = tree;
if( !(tree->left) )tree = tree->right;
else if( !(tree->right) )tree = tree->left;
free(temp);
}
}
return tree;
}
使用gcc编译,指令为:
gcc Code.c -o g生成可执行文件后,输入“./g”进行调用
运行指令如下:
此时已生成如下文件:
使用dot指令:
![]()

3.java+neo4j
在这套组合中,Java的功能是控制neo4j的增删查改。事实上,neo4j支持cyoher查询语言,但在大规模多操作的工作要求下,使用eclipse通过maven管理,jdbc桥接neo4j具有更高的工作效率。
首先展示一下我在很久之前就建立的连接文件。
新建maven项目,在pom.xml中设置如下:
<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
<modelVersion>4.0.0</modelVersion>
<groupId>nd.esp.com</groupId>
<artifactId>maven</artifactId>
<version>0.0.1-SNAPSHOT</version>
<packaging>jar</packaging>
<name>maven</name>
<url>http://maven.apache.org</url>
<properties>
<project.build.sourceEncoding>UTF-8</project.build.sourceEncoding>
</properties>
<!-- Embedded Neo4j依赖,目前最新版本是2.3.3-->
<dependencies>
<dependency>
<groupId>org.neo4j</groupId>
<artifactId>neo4j-slf4j</artifactId>
<version>2.3.3</version>
</dependency>
<dependency>
<groupId>net.sourceforge.javacsv</groupId>
<artifactId>javacsv</artifactId>
<version>2.0</version>
</dependency>
</dependencies>
</project>此时可以查看依赖文件:
我找了一个以前写的代码,内容如下,其中指定graphdb文件位置,也是稍后打开图数据库neo4j的文件。
package csvtoneo4j.maven;
import java.io.File;
import java.io.IOException;
import org.neo4j.graphdb.Direction;
import org.neo4j.graphdb.GraphDatabaseService;
import org.neo4j.graphdb.Label;
import org.neo4j.graphdb.Node;
import org.neo4j.graphdb.Relationship;
import org.neo4j.graphdb.RelationshipType;
import org.neo4j.graphdb.Transaction;
import org.neo4j.graphdb.factory.GraphDatabaseFactory;
import org.neo4j.io.fs.FileUtils;
public class CreateNeo4j {
File storeFile = new File("D:/BeTheBest/stitp/Neo4j/default.graphdb");
public String greeting;
// START SNIPPET: vars
GraphDatabaseService graphDb;
Node firstNode;
Node secondNode;
Relationship relationship;
// END SNIPPET: vars
// START SNIPPET: createReltype
public enum RelTypes implements RelationshipType{
BE_INCLUDED_IN,//国家和地区之间的关系
COME_FROM,//品牌和国家的关系
IS_A_KIND_OF//商品和品牌之间的关系
}
// END SNIPPET: createReltype
// START SNIPPET: createLabeltype
public enum Lables implements Label{
Area,//地区
Country,//国家
Brand,//品牌
Drink//商品
}
// END SNIPPET: createLabeltype
void createDb() throws IOException
{
try {
FileUtils.deleteRecursively(storeFile);
}
catch(IOException e) {
throw new RuntimeException(e);
}
// START SNIPPET: startDb
graphDb = new GraphDatabaseFactory().newEmbeddedDatabase(storeFile);
registerShutdownHook( graphDb);
// END SNIPPET: startDb
// START SNIPPET: transaction
// Embedded Neo4j基本上所有的操作都需要在事务内执行
try ( Transaction tx = graphDb.beginTx() )
{
// Database operations go here
// END SNIPPET: transaction
// START SNIPPET: addData
firstNode = graphDb.createNode();
firstNode.setProperty( "message", "Hello, " );
secondNode = graphDb.createNode();
secondNode.setProperty( "message", "World!" );
relationship = firstNode.createRelationshipTo( secondNode, RelTypes.BE_INCLUDED_IN );
relationship.setProperty( "message", "brave Neo4j " );
// END SNIPPET: addData
// START SNIPPET: readData
System.out.print( firstNode.getProperty( "message" ) );
System.out.print( relationship.getProperty( "message" ) );
System.out.print( secondNode.getProperty( "message" ) );
// END SNIPPET: readData
greeting = ( (String) firstNode.getProperty( "message" ) )
+ ( (String) relationship.getProperty( "message" ) )
+ ( (String) secondNode.getProperty( "message" ) );
// START SNIPPET: transaction
tx.success();
}
// END SNIPPET: transaction
}
// 移除新建的数据
void removeData()
{
try ( Transaction tx = graphDb.beginTx() )
{
// START SNIPPET: removingData
// let's remove the data
firstNode.getSingleRelationship( RelTypes.BE_INCLUDED_IN, Direction.OUTGOING ).delete();
firstNode.delete();
secondNode.delete();
// END SNIPPET: removingData
tx.success();
}
}
// 关闭Neo4j 数据库
void shutDown()
{
System.out.println();
System.out.println( "Shutting down database ..." );
// START SNIPPET: shutdownServer
graphDb.shutdown();
// END SNIPPET: shutdownServer
}
// 为Neo4j 实例注册一个关闭的hook,当VM被强制退出时,Neo4j 实例能够正常关闭
private static void registerShutdownHook( final GraphDatabaseService graphDb )
{
Runtime.getRuntime().addShutdownHook( new Thread()
{
@Override
public void run()
{
graphDb.shutdown();
}
} );
}
public static void main(String[] args) throws IOException {
// TODO Auto-generated method stub
System.out.printf("你一定会成功的\n");
CreateNeo4j c1=new CreateNeo4j();
c1.createDb();
// c1.removeData();
c1.shutDown();
}
}
在eclipse可以使用java语言控制,也可使用cypher,想要详细了解可以找我啊哈哈。cypher的例子在下面,也是之前写的:
package csvtoneo4j.maven;
import java.sql.Connection;
import java.sql.DriverManager;
import java.sql.ResultSet;
import java.sql.SQLException;
import java.sql.Statement;
public class Cypher {
public static void main(String[] args) throws SQLException {
// TODO Auto-generated method stub
Connection con = DriverManager.getConnection("jdbc:neo4j:http://127.0.0.1:7474/","neo4j","neo4jj"); //这里可以使用localhost,最好还是使用ip地址,
//Querying
int b=0;
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("LOAD CSV WITH HEADERS FROM 'file:///Country.csv' AS line MERGE (c:Country{name:line.name})");
b++;
}
while(b==1){
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("LOAD CSV WITH HEADERS FROM 'file:///Area.csv' AS line MERGE (c:Area{name:line.name})");
b++;
}
}
while(b==2){
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("LOAD CSV WITH HEADERS FROM 'file:///Brand.csv' AS line MERGE (c:Brand{name:line.name})");
b++;
}
}
while(b==3){
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("LOAD CSV WITH HEADERS FROM 'file:///data.csv' AS line MERGE (c:Drink{ID:line.ID,Brand:line.Brand,TradeNAme:line.TradeName,GrossWeight:line.GrossWeight,Origin:line.Origin,DomesticOrimport:line.DomesticOrimport,Taste:line.Taste,Classify:line.Classify,Packaging:line.Packaging,WhetherTheSugar:line.WhetherTheSugar,IndividualCapacity:line.IndividualCapacity,ApplicateScene:line.ApplicateScene,ExpirationDate:line.ExpirationDate})");
b++;
}
}
while(b==4){
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("LOAD CSV WITH HEADERS FROM 'file:///5.csv' AS line match(from:Brand{name:line.Brand}),(to:Country{name:line.Origin}) merge (from)-[r:COME_FROM{name:line.guanxi}]->(to)");
b++;
}
}
while(b==5){
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("LOAD CSV WITH HEADERS FROM 'file:///6.csv' AS line match(from:Drink{ID:line.ID}),(to:Brand{name:line.Brand}) merge (from)-[r:IS_A_KIND_OF{name:line.guanxi}]->(to)");
b++;
}
}
while(b==6){
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("LOAD CSV WITH HEADERS FROM 'file:///canda.csv' AS line match(from:Country{name:line.Origin}),(to:Area{name:line.DomesticOrimport}) merge (from)-[r:BE_INCLUDED_IN{name:line.DomesticOrimport}]->(to)");
}
}
}
}
上面的指令中加载文件需要实现放在同文件夹下import文件夹。
运行完毕后,可以打开neo4j桌面版或者社区版,先展示社区版:
社区版分为在命令行中打开相应版本的neo4j,在此之前安装好neo4j,配置环境变量;
也可使用社区版的窗口软件:
前面也提到加入java为了更有效率的完成大工作量,在本次尝试中,使用cypher查询语言进行使用,下面的展示也完全在desktop版本中进行,因为它可以建立多个图数据库,个人有好多项目也是同时在使用neo4j。
首先确立一下思路,树的节点为图的节点,关系边为“左子树”和“右子树”,插入即创建操作,删除和查找操作代入即可。左子树减右子树的值定义为节点的属性。
平衡的调整总结为删除、排序和创建的综合使用,在java中可进行封装,在这边底层实现时细致展现。
尝试如下:
-创建数据库:
-插入 数值6,平衡因子:0
CREATE (n{id:1,weight:6,平衡因子:0}) 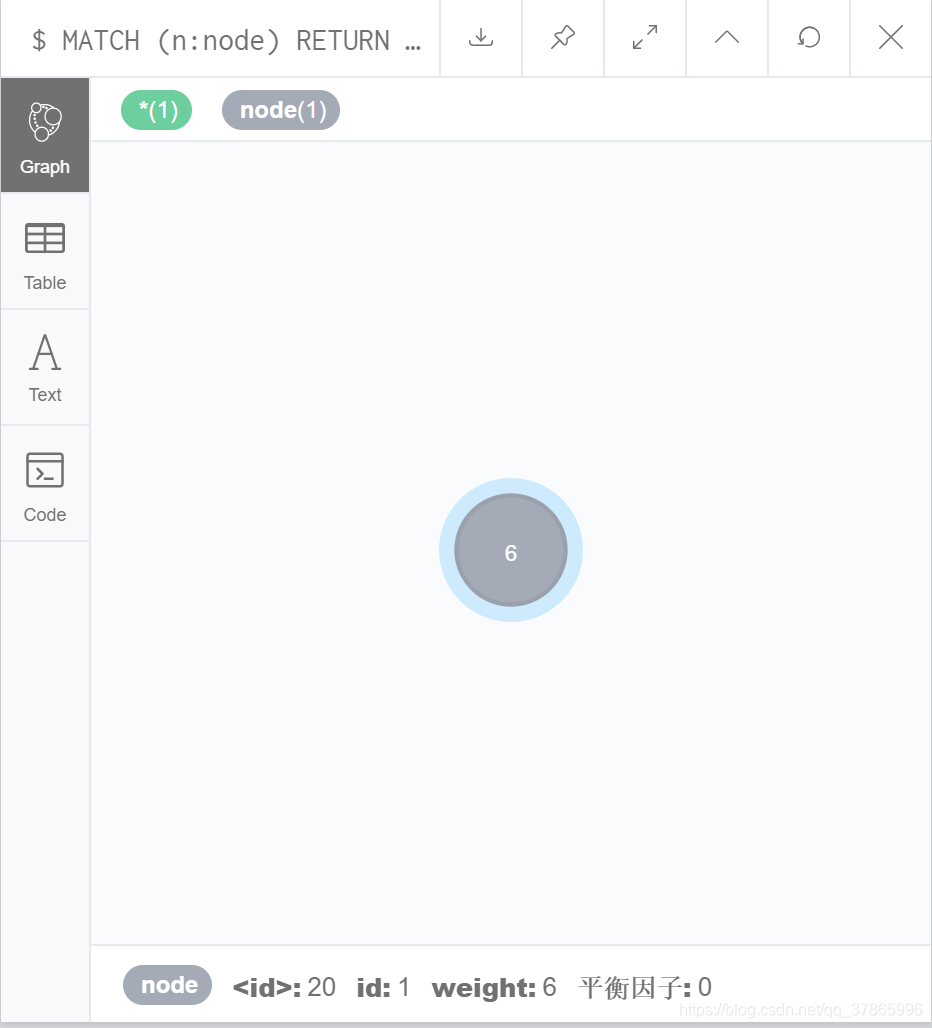
-插入 数值9
(java判断9>6)
创建9
CREATE (n:node{id:2,weight:9,平衡因子:0})MATCH (a:node{weight:6}),(b:node{weight:9}) MERGE (a)-[r:Right]->(b)同时判断节点6的左子树和右子树平衡因子值(无左或右子树都默认为0),相减后为根节点的平衡因子值(java中完成),在Neo4j中使用节点的更新功能对所有节点进行更新:
MATCH (n{weight:6,平衡因子:0}) SET n.平衡因子=-1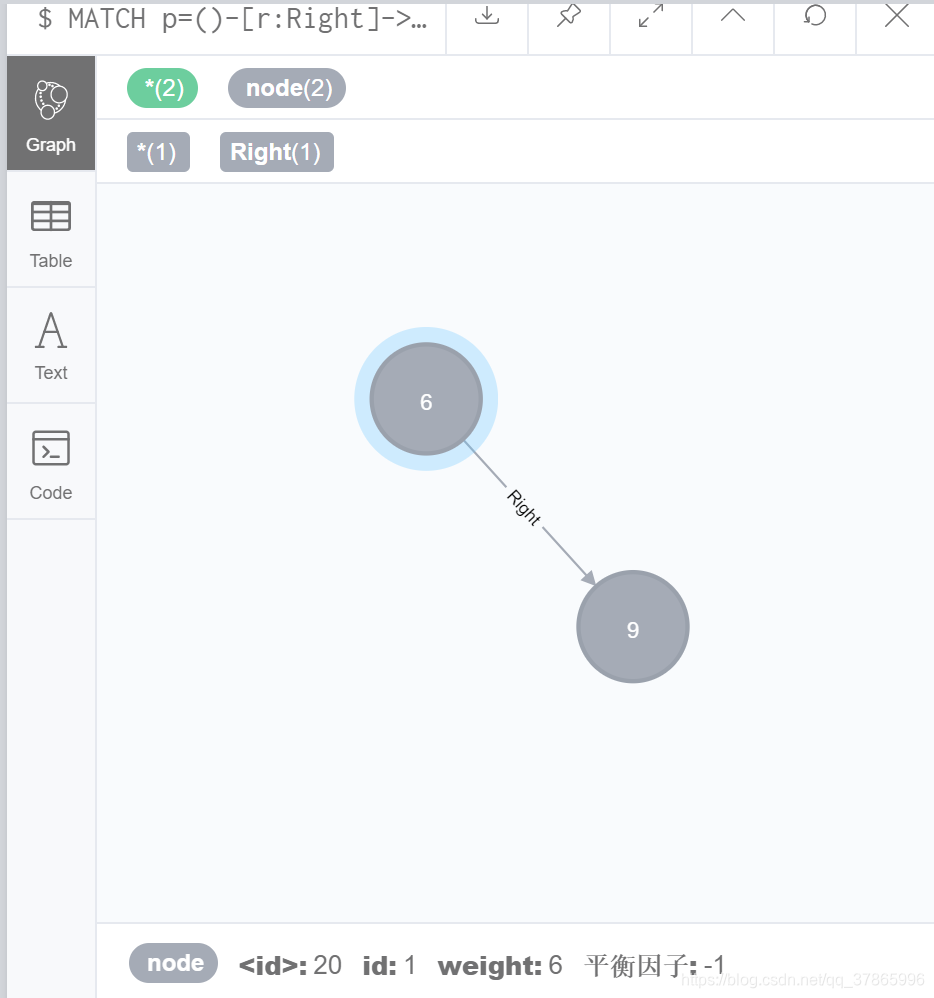
类似建立到判断条件平衡因子大于1或者小于-1,则对以此节点为根节点的最小失衡子树进行调整,调整前如图:
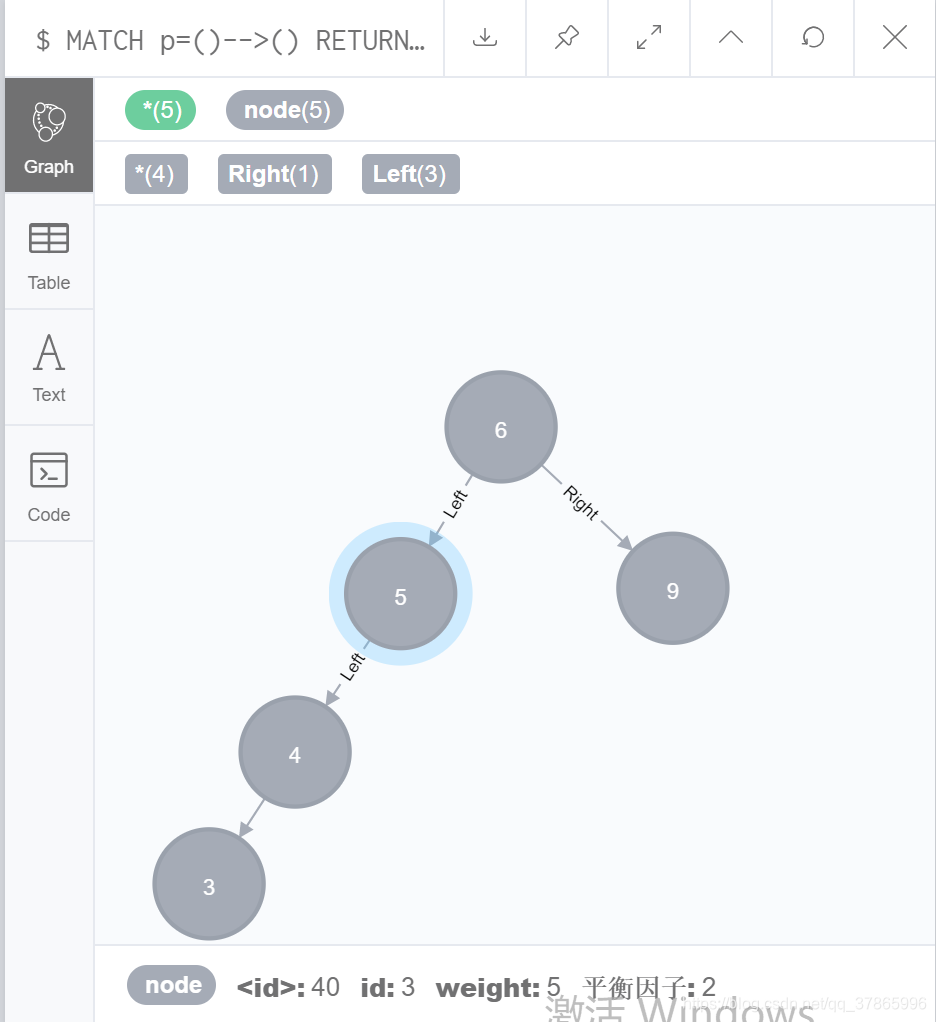
调整LL情况,即在Java 中通过算法对应到,删除6到5的关系边,5到4的关系边(根据二叉树特点巧妙删除所有与5有关的边),建立6到4的关系边,4到5的关系边,并更新平衡因子。此处展示删除语句:
MATCH (a)-[r]-(b) WHERE a.weight=5 DELETE r
调整完毕后,动态展示为:
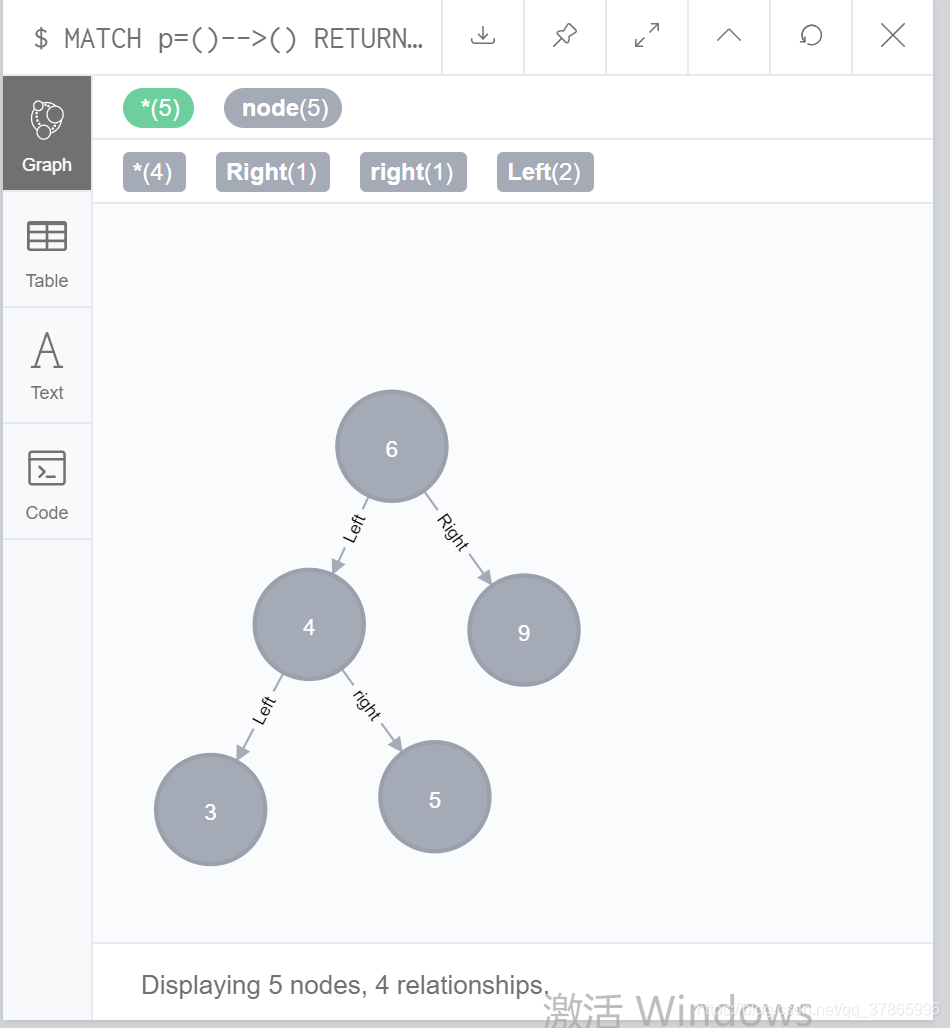
基于实验产生结果、理论得到实践的目的,因时间不足,暂做以下算法思想:
基于平衡二叉树的代码,在调整后加入层次遍历的代码,层次遍历的思想是宽度优先遍历,然后在遍历的过程中是进行左子树和右子树的判断的,由此继续加入的代码为先在neo4j生成根节点,如果左子树存在,就生成左子树的节点,并生成两节点之间的关系边,右子树同理。最后的代码为:
package avlTree;
import java.sql.Connection;
import java.sql.DriverManager;
import java.sql.ResultSet;
import java.sql.SQLException;
import java.sql.Statement;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Scanner;
import java.util.Iterator;
import java.util.NoSuchElementException;
import java.util.Queue;
public class AVLTree<E> {
private Entry<E> root = null;//根节点
private int size = 0;//树中元素个数
public AVLTree(){
}
public int size(){
return size;
}
/**
* @param p 最小旋转子树的根节点
* 向左旋转之后p移到p的左子树处,p的右子树B变为此最小子树根节点,
* B的左子树变为p的右子树
* 比如: A(-2) B(1)
* \ 左旋转 / \
* B(0) ----> A(0) \
* / \ \ \
* BL(0) BR(0) BL(0) BR(0)
* 旋转之后树的深度之差不超过1
*/
private void rotateLeft(Entry<E> p) {
if(p!=null){
Entry<E> r = p.right;
p.right = r.left; //把p右子树的左节点嫁接到p的右节点,如上图,把BL作为A的右子节点
if (r.left != null) //如果B的左节点BL不为空,把BL的父节点设为A
r.left.parent = p;
r.parent = p.parent; //A的父节点设为B的父节点
if (p.parent == null) //如果p是根节点
root = r; //r变为父节点,即B为父节点
else if (p.parent.left == p) //如果p是左子节点
p.parent.left = r; //p的父节点的左子树为r
else //如果p是右子节点
p.parent.right = r; //p的父节点的右子树为r
r.left = p; //p变为r的左子树,即A为B的左子树
p.parent = r; //同时更改p的父节点为r,即A的父节点为B
}
}
/**
* @param p 最小旋转子树的根节点
* 向右旋转之后,p移到p的右子节点处,p的左子树B变为最小旋转子树的根节点
* B的右子节点变为p的左节点、
* 例如: A(2) B(-1)
* / 右旋转 / \
* B(0) ------> / A(0)
* / \ / /
* BL(0) BR(0) BL(0) BR(0)
*/
private void rotateRight(Entry<E> p){
System.out.println("绕"+p.element+"右旋");
if(p!=null){
Entry<E> l = p.left;
p.left = l.right; //把B的右节点BR作为A的左节点
if (l.right != null) //如果BR不为null,设置BR的父节点为A
l.right.parent = p;
l.parent = p.parent; //A的父节点赋给B的父节点
if (p.parent == null) //如果p是根节点
root = l; //B为根节点
else if (p.parent.right == p) //如果A是其父节点的左子节点
p.parent.right = l; //B为A的父节点的左子树
else //如果A是其父节点的右子节点
p.parent.left = l; //B为A的父节点的右子树
l.right = p; //A为B的右子树
p.parent = l; //设置A的父节点为B
}
}
/**
* 平衡而二叉树的插入操作
* 基本原理为:
* 1.首先如同二叉排序树一般,找到其要插入的节点的位置,并把元素插入其中;
* 2.自下向上进行回溯,回溯做两个事情:
* (1)其一是修改祖先节点的平衡因子,当插入 一个节点时只有根节点到插入节点
* 的路径中的节点的平衡因子会被改变,而且改变的原则是当插入节点在某节点(称为A)
* 的左子树 中时,A的平衡因子(称为BF)为BF+1,当插入节点在A的右子树中时A的BF-1,
* 而判断插入节点在左子树中还是右子树中只要简单的比较它与A的大小
* (2)在改变祖先节点的平衡因子的同时,找到最近一个平衡因子大于2或小于-2的节点,
* 从这个节点开始调整最小不平衡树进行旋转调整,关于如何调整见下文。
* 由于调整后,最小不平衡子树的高度与插入节点前的高度相同,故不需继续要调整祖先节点。
* 这里还有一个特殊情况,如果调整BF时,发现某个节点的BF变为0了,则停止向上继续调整,
* 因为这表明此节点中高度小的子树增加了新节点,高度不变,那么祖先节点的BF自然不变。
*
*
*/
public boolean add(E element){
Entry<E> t = root;
if(t == null){
root = new Entry<E>(element,null);
size = 1;
return true;
}
int cmp;
Entry<E> parent; //保存t的父节点
Comparable<? super E> e = (Comparable<? super E>) element;
//从根节点向下搜索,找到插入位置
do {
parent = t;
cmp = e.compareTo(t.element);
if(cmp < 0){
t = t.left;
}else if(cmp > 0){
t = t.right;
}else{
return false;
}
} while (t!=null);
Entry<E> child = new Entry(element,parent);
if(cmp < 0){
parent.left = child;
}else{
parent.right = child;
}
//自下向上回溯,查找最近不平衡节点
while(parent!=null){
cmp = e.compareTo(parent.element);
if(cmp < 0){ //插入节点在parent的左子树中
parent.balance++;
}else{ //插入节点在parent的右子树中
parent.balance--;
}
if(parent.balance == 0){ //此节点的balance为0,不再向上调整BF值,且不需要旋转
break;
}
if(Math.abs(parent.balance) == 2){ //找到最小不平衡子树根节点
fixAfterInsertion(parent);
break; //不用继续向上回溯
}
parent = parent.parent;
}
size ++;
return true;
}
/**
* 调整的方法:
* 1.当最小不平衡子树的根(以下简称R)为2时,即左子树高于右子树:
* 如果R的左子树的根节点的BF为1时,做右旋;
* 如果R的左子树的根节点的BF为-1时,先左旋然后再右旋
*
* 2.R为-2时,即右子树高于左子树:
* 如果R的右子树的根节点的BF为1时,先右旋后左旋
* 如果R的右子树的根节点的BF为-1时,做左旋
*
* 至于调整之后,各节点的BF变化见代码
*/
private void fixAfterInsertion(Entry<E> p){
if(p.balance == 2){
leftBalance(p);
}
if(p.balance == -2){
rightBalance(p);
}
}
/**
* 做左平衡处理
* 平衡因子的调整如图:
* t rd
* / \ / \
* l tr 左旋后右旋 l t
* / \ -------> / \ / \
* ll rd ll rdl rdr tr
* / \
* rdl rdr
*
* 情况2(rd的BF为0)
*
*
* t rd
* / \ / \
* l tr 左旋后右旋 l t
* / \ -------> / \ \
* ll rd ll rdl tr
* /
* rdl
*
* 情况1(rd的BF为1)
*
*
* t rd
* / \ / \
* l tr 左旋后右旋 l t
* / \ -------> / / \
* ll rd ll rdr tr
* \
* rdr
*
* 情况3(rd的BF为-1)
*
*
* t l
* / 右旋处理 / \
* l ------> ll t
* / \ /
* ll rd rd
* 情况4(L等高)
*/
private boolean leftBalance(Entry<E> t){
boolean heightLower = true;
Entry<E> l = t.left;
switch (l.balance) {
case LH: //左高,右旋调整,旋转后树的高度减小
t.balance = l.balance = EH;
rotateRight(t);
break;
case RH: //右高,分情况调整
Entry<E> rd = l.right;
switch (rd.balance) { //调整各个节点的BF
case LH: //情况1
t.balance = RH;
l.balance = EH;
break;
case EH: //情况2
t.balance = l.balance = EH;
break;
case RH: //情况3
t.balance = EH;
l.balance = LH;
break;
}
rd.balance = EH;
rotateLeft(t.left);
rotateRight(t);
break;
case EH: //特殊情况4,这种情况在添加时不可能出现,只在移除时可能出现,旋转之后整体树高不变
l.balance = RH;
t.balance = LH;
rotateRight(t);
heightLower = false;
break;
}
return heightLower;
}
/**
* 做右平衡处理
* 平衡因子的调整如图:
* t ld
* / \ / \
* tl r 先右旋再左旋 t r
* / \ --------> / \ / \
* ld rr tl ldl ldr rr
* / \
* ldl ldr
* 情况2(ld的BF为0)
*
* t ld
* / \ / \
* tl r 先右旋再左旋 t r
* / \ --------> / \ \
* ld rr tl ldl rr
* /
* ldl
* 情况1(ld的BF为1)
*
* t ld
* / \ / \
* tl r 先右旋再左旋 t r
* / \ --------> / / \
* ld rr tl ldr rr
* \
* ldr
* 情况3(ld的BF为-1)
*
* t r
* \ 左旋 / \
* r -------> t rr
* / \ \
* ld rr ld
* 情况4(r的BF为0)
*/
private boolean rightBalance(Entry<E> t){
boolean heightLower = true;
Entry<E> r = t.right;
switch (r.balance) {
case LH: //左高,分情况调整
Entry<E> ld = r.left;
switch (ld.balance) { //调整各个节点的BF
case LH: //情况1
t.balance = EH;
r.balance = RH;
break;
case EH: //情况2
t.balance = r.balance = EH;
break;
case RH: //情况3
t.balance = LH;
r.balance = EH;
break;
}
ld.balance = EH;
rotateRight(t.right);
rotateLeft(t);
break;
case RH: //右高,左旋调整
t.balance = r.balance = EH;
rotateLeft(t);
break;
case EH: //特殊情况4
r.balance = LH;
t.balance = RH;
rotateLeft(t);
heightLower = false;
break;
}
return heightLower;
}
/**
* 查找指定元素,如果找到返回其Entry对象,否则返回null
*/
private Entry<E> getEntry(Object element) {
Entry<E> tmp = root;
Comparable<? super E> e = (Comparable<? super E>) element;
int c;
while (tmp != null) {
c = e.compareTo(tmp.element);
if (c == 0) {
return tmp;
} else if (c < 0) {
tmp = tmp.left;
} else {
tmp = tmp.right;
}
}
return null;
}
/**
* 平衡二叉树的移除元素操作
*
*/
public boolean remove(Object o){
Entry<E> e = getEntry(o);
if(e!=null){
deleteEntry(e);
return true;
}
return false;
}
private void deleteEntry(Entry<E> p){
size --;
//如果p左右子树都不为空,找到其直接后继,替换p,之后p指向s,删除p其实是删除s
//所有的删除左右子树不为空的节点都可以调整为删除左右子树有其一不为空,或都为空的情况。
if (p.left != null && p.right != null) {
Entry<E> s = successor(p);
p.element = s.element;
p = s;
}
Entry<E> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) { //如果其左右子树有其一不为空
replacement.parent = p.parent;
if (p.parent == null) //如果p为root节点
root = replacement;
else if (p == p.parent.left) //如果p是左孩子
p.parent.left = replacement;
else //如果p是右孩子
p.parent.right = replacement;
p.left = p.right = p.parent = null; //p的指针清空
//这里更改了replacement的父节点,所以可以直接从它开始向上回溯
fixAfterDeletion(replacement);
} else if (p.parent == null) { // 如果全树只有一个节点
root = null;
} else { //左右子树都为空
fixAfterDeletion(p); //这里从p开始回溯
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
/**
* 返回以中序遍历方式遍历树时,t的直接后继
*/
static <E> Entry<E> successor(Entry<E> t) {
if (t == null)
return null;
else if (t.right != null) { //往右,然后向左直到尽头
Entry<E> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { //right为空,如果t是p的左子树,则p为t的直接后继
Entry<E> p = t.parent;
Entry<E> ch = t;
while (p != null && ch == p.right) { //如果t是p的右子树,则继续向上搜索其直接后继
ch = p;
p = p.parent;
}
return p;
}
}
/**
* 删除某节点p后的调整方法:
* 1.从p开始向上回溯,修改祖先的BF值,这里只要调整从p的父节点到根节点的BF值,
* 调整原则为,当p位于某祖先节点(简称A)的左子树中时,A的BF减1,当p位于A的
* 右子树中时A的BF加1。当某个祖先节点BF变为1或-1时停止回溯,这里与插入是相反的,
* 因为原本这个节点是平衡的,删除它的子树的某个节点并不会改变它的高度
*
* 2.检查每个节点的BF值,如果为2或-2需要进行旋转调整,调整方法如下文,
* 如果调整之后这个最小子树的高度降低了,那么必须继续从这个最小子树的根节点(假设为B)继续
* 向上回溯,这里和插入不一样,因为B的父节点的平衡性因为其子树B的高度的改变而发生了改变,
* 那么就可能需要调整,所以删除可能进行多次的调整。
*
*/
private void fixAfterDeletion(Entry<E> p){
boolean heightLower = true; //看最小子树调整后,它的高度是否发生变化,如果减小,继续回溯
Entry<E> t = p.parent;
Comparable<? super E> e = (Comparable<? super E>)p.element;
int cmp;
//自下向上回溯,查找不平衡的节点进行调整
while(t!=null && heightLower){
cmp = e.compareTo(t.element);
/**
* 删除的节点是右子树,等于的话,必然是删除的某个节点的左右子树不为空的情况
* 例如: 10
* / \
* 5 15
* / \
* 3 6
* 这里删除5,是把6的值赋给5,然后删除6,这里6是p,p的父节点的值也是6。
* 而这也是右子树的一种
*/
if(cmp >= 0 ){
t.balance ++;
}else{
t.balance --;
}
if(Math.abs(t.balance) == 1){ //父节点经过调整平衡因子后,如果为1或-1,说明调整之前是0,停止回溯。
break;
}
Entry<E> r = t;
//这里的调整跟插入一样
if(t.balance == 2){
heightLower = leftBalance(r);
}else if(t.balance==-2){
heightLower = rightBalance(r);
}
t = t.parent;
}
}
private static final int LH = 1; //左高
private static final int EH = 0; //等高
private static final int RH = -1; //右高
/**
* 树节点,为方便起见不写get,Set方法
*/
static class Entry<E>{
E element;
Entry<E> parent;
Entry<E> left;
Entry<E> right;
int balance = EH; //平衡因子,只能为1或0或-1
public Entry(E element,Entry<E> parent){
this.element = element;
this.parent = parent;
}
public Entry(){}
@Override
public String toString() {
return element+" BF="+balance;
}
}
public static void BFSOrder(Entry t)
{
try {
Connection con = DriverManager.getConnection("jdbc:neo4j:http://127.0.0.1:7474/","neo4j","neo4jj");
//使用jdbc连接neo4j
if(t==null) return ;
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("CREATE (Weight:"+t.element+") RETURN n ");
while(rs.next())
{
System.out.println(rs.getString("n"));
}
}
Queue<Entry> queue = new ArrayDeque<Entry>();
queue.offer(t); //进入队列
while(!queue.isEmpty())
{
t=queue.poll(); //当前节点出队列
System.out.print(t.element);
if(t.left!=null) //当前节点左孩子去排队,在前面哦
{queue.offer(t.left);
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("CREATE (Weight:"+t.left.element+") RETURN n ");
while(rs.next())
{
System.out.println(rs.getString("n"));
}
}
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("MATCH (a{Weight="+t.element+"}),(b{Weight="+t.left.element+"})MERGE (a)-[name:左子树]->(b) ");
while(rs.next())
{
System.out.println(rs.getString("n"));
}
}}
if(t.right!=null) //右孩子排第二
{ queue.offer(t.right);
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("CREATE (Weight:"+t.right.element+") RETURN n ");
while(rs.next())
{
System.out.println(rs.getString("n"));
}
}
try(Statement stmt = con.createStatement())
{
ResultSet rs = stmt.executeQuery("MATCH (a{Weight="+t.element+"}),(b{Weight="+t.right.element+"})MERGE (a)-[name:右子树]->(b) ");
while(rs.next())
{
System.out.println(rs.getString("n"));
}
}
}
}
} catch (SQLException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
//返回中序遍历此树的迭代器,返回的是一个有序列表
private class BinarySortIterator implements Iterator<E>{
Entry<E> next;
Entry<E> lastReturned;
public BinarySortIterator(){
Entry<E> s = root;
if(s !=null){
while(s.left != null){ //找到中序遍历的第一个元素
s = s.left;
}
}
next = s; //赋给next
}
@Override
public boolean hasNext() {
return next!=null;
}
@Override
public E next() {
Entry<E> e = next;
if (e == null)
throw new NoSuchElementException();
next = successor(e);
lastReturned = e;
return e.element;
}
@Override
public void remove() {
if (lastReturned == null)
throw new IllegalStateException();
// deleted entries are replaced by their successors
if (lastReturned.left != null && lastReturned.right != null)
next = lastReturned;
deleteEntry(lastReturned);
lastReturned = null;
}
}
public Iterator<E> itrator(){
return new BinarySortIterator();
}
private int treeHeight(Entry<E> p){
if(p == null){
return -1;
}
return 1 + Math.max(treeHeight(p.left), treeHeight(p.right));
}
//测试,你也可以任意测试
public static void main(String[] args) {
AVLTree<Integer> tree = new AVLTree<Integer>();
System.out.println("------添加------");
int w=1;
while(w!=0)
{
Scanner s1=new Scanner(System.in);
w=s1.nextInt();
tree.add(w);
};
// System.out.println("------删除------");
// tree.remove(50);
// tree.remove(66);
//
System.out.println();
tree.BFSOrder(tree.root);
// Iterator<Integer> it = tree.itrator();
// while(it.hasNext()){
// System.out.print(it.next()+" ");
// }
}
}
Cypher语言不允许多条语句并发执行,因此可使用d++,根据d的值逐步执行。
如果使用Java语言进行Neo4j的使用,则不会出现这种情况。
九、阶段七:图形显示B-树
十、阶段八:动态显示B-树
结合以前的博客,通过查找相关的文档,找到了些关于B-树显示的代码:
参考博客:https://blog.youkuaiyun.com/geek_jerome/article/details/78895289
代码里面加入了一些自己的思考
BTree.h
//
// BTree.h
// B-Tree2
//
// Created by 张立鹏 on 2018/11/2.
// Copyright © 2018年 张立鹏. All rights reserved.
//
#ifndef _BTREE_H
#define _BTREE_H
#define MAXM 10 //定义B树的最大的阶数
const int m=4; //设定B树的阶数
const int Max=m-1; //结点的最大关键字数量
const int Min=(m-1)/2; //结点的最小关键字数量
typedef int KeyType; //KeyType为关键字类型
typedef struct node{ //B树和B树结点类型
int keynum; //结点关键字个数
KeyType key[MAXM]; //关键字数组,key[0]不使用
struct node *parent; //双亲结点指针
struct node *ptr[MAXM]; //孩子结点指针数组
}BTNode,*BTree;
typedef struct{ //B树查找结果类型
BTNode *pt; //指向找到的结点
int i; //在结点中的关键字位置;
int tag; //查找成功与否标志
}Result;
typedef struct LNode{ //链表和链表结点类型
BTree data; //数据域
struct LNode *next; //指针域
}LNode, *LinkList;
typedef enum status{ //枚举类型(依次递增)
TRUE,
FALSE,
OK,
ERROR,
OVERFLOW,
EMPTY
}Status;
Status InitBTree(BTree &t); //初始化B树
int SearchBTNode(BTNode *p,KeyType k); //在结点p中查找关键字k的插入位置i
Result SearchBTree(BTree t,KeyType k); /*在树t上查找关键字k,返回结果(pt,i,tag)。若查找成功,则特征值
tag=1,关键字k是指针pt所指结点中第i个关键字;否则特征值tag=0,
关键字k的插入位置为pt结点的第i个*/
void InsertBTNode(BTNode *&p,int i,KeyType k,BTNode *q); //将关键字k和结点q分别插入到p->key[i+1]和p->ptr[i+1]中
void SplitBTNode(BTNode *&p,BTNode *&q); //将结点p分裂成两个结点,前一半保留,后一半移入结点q
void NewRoot(BTNode *&t,KeyType k,BTNode *p,BTNode *q); //生成新的根结点t,原结点p和结点q为子树指针
void InsertBTree(BTree &t,int i,KeyType k,BTNode *p); /*在树t上结点q的key[i]与key[i+1]之间插入关键字k。若引起
结点过大,则沿双亲链进行必要的结点分裂调整,使t仍是B树*/
void Remove(BTNode *p,int i); //从p结点删除key[i]和它的孩子指针ptr[i]
void Substitution(BTNode *p,int i); //查找被删关键字p->key[i](在非叶子结点中)的替代叶子结点(右子树中值最小的关键字)
void MoveRight(BTNode *p,int i); /*将双亲结点p中的最后一个关键字移入右结点q中
将左结点aq中的最后一个关键字移入双亲结点p中*/
void MoveLeft(BTNode *p,int i); /*将双亲结点p中的第一个关键字移入结点aq中,
将结点q中的第一个关键字移入双亲结点p中*/
void Combine(BTNode *p,int i); /*将双亲结点p、右结点q合并入左结点aq,
并调整双亲结点p中的剩余关键字的位置*/
void AdjustBTree(BTNode *p,int i); //删除结点p中的第i个关键字后,调整B树
int FindBTNode(BTNode *p,KeyType k,int &i); //反映是否在结点p中是否查找到关键字k
int BTNodeDelete(BTNode *p,KeyType k); //在结点p中查找并删除关键字k
void BTreeDelete(BTree &t,KeyType k); //构建删除框架,执行删除操作
void DestroyBTree(BTree &t); //递归释放B树
Status InitQueue(LinkList &L); //初始化队列
LNode* CreateNode(BTree t); //新建一个结点
Status Enqueue(LNode *p,BTree t); //元素q入队列
Status Dequeue(LNode *p,BTNode *&q); //出队列,并以q返回值
Status IfEmpty(LinkList L); //队列判空
void DestroyQueue(LinkList L); //销毁队列
Status Traverse(BTree t,LinkList L,int newline,int sum); //用队列遍历输出B树
Status PrintBTree(BTree t); //输出B树
void Test(); //测试B树功能函数
#endif /* BTree_h */
main.cpp
//
// main.cpp
// B-Tree2
//
// Created by 张立鹏 on 2018/11/2.
// Copyright © 2018年 张立鹏. All rights reserved.
//
#include"BTree.h"
#include <stdio.h>
#include <sys/malloc.h>
#include <stdlib.h>
Status InitBTree(BTree &t){
//初始化B树
t=NULL;
return OK;
}
int SearchBTNode(BTNode *p,KeyType k){
//在结点p中查找关键字k的插入位置i
int i=0;
for(i=0;i<p->keynum&&p->key[i+1]<=k;i++);
return i;
}
Result SearchBTree(BTree t,KeyType k){
/*在树t上查找关键字k,返回结果(pt,i,tag)。若查找成功,则特征值
tag=1,关键字k是指针pt所指结点中第i个关键字;否则特征值tag=0,
关键字k的插入位置为pt结点的第i个*/
BTNode *p=t,*q=NULL; //初始化结点p和结点q,p指向待查结点,q指向p的双亲
int found_tag=0; //设定查找成功与否标志
int i=0;
Result r; //设定返回的查找结果
while(p!=NULL&&found_tag==0){
i=SearchBTNode(p,k); //在结点p中查找关键字k,使得p->key[i]<=k<p->key[i+1]
if(i>0&&p->key[i]==k) //找到待查关键字
found_tag=1; //查找成功
else{ //查找失败
q=p;
p=p->ptr[i];
}
}
if(found_tag==1){ //查找成功
r.pt=p;
r.i=i;
r.tag=1;
}
else{ //查找失败
r.pt=q;
r.i=i;
r.tag=0;
}
return r; //返回关键字k的位置(或插入位置)
}
void InsertBTNode(BTNode *&p,int i,KeyType k,BTNode *q){
//将关键字k和结点q分别插入到p->key[i+1]和p->ptr[i+1]中
int j;
for(j=p->keynum;j>i;j--){ //整体后移空出一个位置
p->key[j+1]=p->key[j];
p->ptr[j+1]=p->ptr[j];
}
p->key[i+1]=k;
p->ptr[i+1]=q;
if(q!=NULL)
q->parent=p;
p->keynum++;
}
void SplitBTNode(BTNode *&p,BTNode *&q){
//将结点p分裂成两个结点,前一半保留,后一半移入结点q
int i;
int s=(m+1)/2;
q=(BTNode *)malloc(sizeof(BTNode)); //给结点q分配空间
q->ptr[0]=p->ptr[s]; //后一半移入结点q
for(i=s+1;i<=m;i++){
q->key[i-s]=p->key[i];
q->ptr[i-s]=p->ptr[i];
}
q->keynum=p->keynum-s;
q->parent=p->parent;
for(i=0;i<=p->keynum-s;i++) //修改双亲指针
if(q->ptr[i]!=NULL)
q->ptr[i]->parent=q;
p->keynum=s-1; //结点p的前一半保留,修改结点p的keynum
}
void NewRoot(BTNode *&t,KeyType k,BTNode *p,BTNode *q){
//生成新的根结点t,原p和q为子树指针
t=(BTNode *)malloc(sizeof(BTNode)); //分配空间
t->keynum=1;
t->ptr[0]=p;
t->ptr[1]=q;
t->key[1]=k;
if(p!=NULL) //调整结点p和结点q的双亲指针
p->parent=t;
if(q!=NULL)
q->parent=t;
t->parent=NULL;
}
void InsertBTree(BTree &t,int i,KeyType k,BTNode *p){
/*在树t上结点q的key[i]与key[i+1]之间插入关键字k。若引起
结点过大,则沿双亲链进行必要的结点分裂调整,使t仍是B树*/
BTNode *q;
int finish_tag,newroot_tag,s; //设定需要新结点标志和插入完成标志
KeyType x;
if(p==NULL) //t是空树
NewRoot(t,k,NULL,NULL); //生成仅含关键字k的根结点t
else{
x=k;
q=NULL;
finish_tag=0;
newroot_tag=0;
while(finish_tag==0&&newroot_tag==0){
InsertBTNode(p,i,x,q); //将关键字x和结点q分别插入到p->key[i+1]和p->ptr[i+1]
if (p->keynum<=Max)
finish_tag=1; //插入完成
else{
s=(m+1)/2;
SplitBTNode(p,q); //分裂结点
x=p->key[s];
if(p->parent){ //查找x的插入位置
p=p->parent;
i=SearchBTNode(p, x);
}
else //没找到x,需要新结点
newroot_tag=1;
}
}
if(newroot_tag==1) //根结点已分裂为结点p和q
NewRoot(t,x,p,q); //生成新根结点t,p和q为子树指针
}
}
void Remove(BTNode *p,int i){
//从p结点删除key[i]和它的孩子指针ptr[i]
int j;
for(j=i+1;j<=p->keynum;j++){ //前移删除key[i]和ptr[i]
p->key[j-1]=p->key[j];
p->ptr[j-1]=p->ptr[j];
}
p->keynum--;
}
void Substitution(BTNode *p,int i){
//查找被删关键字p->key[i](在非叶子结点中)的替代叶子结点(右子树中值最小的关键字)
BTNode *q;
for(q=p->ptr[i];q->ptr[0]!=NULL;q=q->ptr[0]);
p->key[i]=q->key[1]; //复制关键字值
}
void MoveRight(BTNode *p,int i){
/*将双亲结点p中的最后一个关键字移入右结点q中
将左结点aq中的最后一个关键字移入双亲结点p中*/
int j;
BTNode *q=p->ptr[i];
BTNode *aq=p->ptr[i-1];
for(j=q->keynum;j>0;j--){ //将右兄弟q中所有关键字向后移动一位
q->key[j+1]=q->key[j];
q->ptr[j+1]=q->ptr[j];
}
q->ptr[1]=q->ptr[0]; //从双亲结点p移动关键字到右兄弟q中
q->key[1]=p->key[i];
q->keynum++;
p->key[i]=aq->key[aq->keynum]; //将左兄弟aq中最后一个关键字移动到双亲结点p中
p->ptr[i]->ptr[0]=aq->ptr[aq->keynum];
aq->keynum--;
}
void MoveLeft(BTNode *p,int i){
/*将双亲结点p中的第一个关键字移入左结点aq中,
将右结点q中的第一个关键字移入双亲结点p中*/
int j;
BTNode *aq=p->ptr[i-1];
BTNode *q=p->ptr[i];
aq->keynum++; //把双亲结点p中的关键字移动到左兄弟aq中
aq->key[aq->keynum]=p->key[i];
aq->ptr[aq->keynum]=p->ptr[i]->ptr[0];
p->key[i]=q->key[1]; //把右兄弟q中的关键字移动到双亲节点p中
q->ptr[0]=q->ptr[1];
q->keynum--;
for(j=1;j<=aq->keynum;j++){ //将右兄弟q中所有关键字向前移动一位
aq->key[j]=aq->key[j+1];
aq->ptr[j]=aq->ptr[j+1];
}
}
void Combine(BTNode *p,int i){
/*将双亲结点p、右结点q合并入左结点aq,
并调整双亲结点p中的剩余关键字的位置*/
int j;
BTNode *q=p->ptr[i];
BTNode *aq=p->ptr[i-1];
aq->keynum++; //将双亲结点的关键字p->key[i]插入到左结点aq
aq->key[aq->keynum]=p->key[i];
aq->ptr[aq->keynum]=q->ptr[0];
for(j=1;j<=q->keynum;j++){ //将右结点q中的所有关键字插入到左结点aq
aq->keynum++;
aq->key[aq->keynum]=q->key[j];
aq->ptr[aq->keynum]=q->ptr[j];
}
for(j=i;j<p->keynum;j++){ //将双亲结点p中的p->key[i]后的所有关键字向前移动一位
p->key[j]=p->key[j+1];
p->ptr[j]=p->ptr[j+1];
}
p->keynum--; //修改双亲结点p的keynum值
free(q); //释放空右结点q的空间
}
void AdjustBTree(BTNode *p,int i){
//删除结点p中的第i个关键字后,调整B树
if(i==0) //删除的是最左边关键字
if(p->ptr[1]->keynum>Min) //右结点可以借
MoveLeft(p,1);
else //右兄弟不够借
Combine(p,1);
else if(i==p->keynum) //删除的是最右边关键字
if(p->ptr[i-1]->keynum>Min) //左结点可以借
MoveRight(p,i);
else //左结点不够借
Combine(p,i);
else if(p->ptr[i-1]->keynum>Min) //删除关键字在中部且左结点够借
MoveRight(p,i);
else if(p->ptr[i+1]->keynum>Min) //删除关键字在中部且右结点够借
MoveLeft(p,i+1);
else //删除关键字在中部且左右结点都不够借
Combine(p,i);
}
int FindBTNode(BTNode *p,KeyType k,int &i){
//反映是否在结点p中是否查找到关键字k
if(k<p->key[1]){ //结点p中查找关键字k失败
i=0;
return 0;
}
else{ //在p结点中查找
i=p->keynum;
while(k<p->key[i]&&i>1)
i--;
if(k==p->key[i]) //结点p中查找关键字k成功
return 1;
}
return 0;
}
int BTNodeDelete(BTNode *p,KeyType k){
//在结点p中查找并删除关键字k
int i;
int found_tag; //查找标志
if(p==NULL)
return 0;
else{
found_tag=FindBTNode(p,k,i); //返回查找结果
if(found_tag==1){ //查找成功
if(p->ptr[i-1]!=NULL){ //删除的是非叶子结点
Substitution(p,i); //寻找相邻关键字(右子树中最小的关键字)
BTNodeDelete(p->ptr[i],p->key[i]); //执行删除操作
}
else
Remove(p,i); //从结点p中位置i处删除关键字
}
else
found_tag=BTNodeDelete(p->ptr[i],k); //沿孩子结点递归查找并删除关键字k
if(p->ptr[i]!=NULL)
if(p->ptr[i]->keynum<Min) //删除后关键字个数小于MIN
AdjustBTree(p,i); //调整B树
return found_tag;
}
}
void BTreeDelete(BTree &t,KeyType k){
//构建删除框架,执行删除操作
BTNode *p;
int a=BTNodeDelete(t,k); //删除关键字k
if(a==0) //查找失败
printf(" 关键字%d不在B树中\n",k);
else if(t->keynum==0){ //调整
p=t;
t=t->ptr[0];
free(p);
}
}
void DestroyBTree(BTree &t){
//递归释放B树
int i;
BTNode* p=t;
if(p!=NULL){ //B树不为空
for(i=0;i<=p->keynum;i++){ //递归释放每一个结点
DestroyBTree(*&p->ptr[i]);
}
free(p);
}
t=NULL;
}
Status InitQueue(LinkList &L){
//初始化队列
L=(LNode*)malloc(sizeof(LNode)); //分配结点空间
if(L==NULL) //分配失败
return OVERFLOW;
L->next=NULL;
return OK;
}
LNode* CreateNode(BTNode *p){
//新建一个结点
LNode *q;
q=(LNode*)malloc(sizeof(LNode)); //分配结点空间
if(q!=NULL){ //分配成功
q->data=p;
q->next=NULL;
}
return q;
}
Status Enqueue(LNode *p,BTNode *q){
//元素q入队列
if(p==NULL)
return ERROR;
while(p->next!=NULL) //调至队列最后
p=p->next;
p->next=CreateNode(q); //生成结点让q进入队列
return OK;
}
Status Dequeue(LNode *p,BTNode *&q){
//出队列,并以q返回值
LNode *aq;
if(p==NULL||p->next==NULL) //删除位置不合理
return ERROR;
aq=p->next; //修改被删结点aq的指针域
p->next=aq->next;
q=aq->data;
free(aq); //释放结点aq
return OK;
}
Status IfEmpty(LinkList L){
//队列判空
if(L==NULL) //队列不存在
return ERROR;
if(L->next==NULL) //队列为空
return TRUE;
return FALSE; //队列非空
}
void DestroyQueue(LinkList L){
//销毁队列
LinkList p;
if(L!=NULL){
p=L;
L=L->next;
free(p); //逐一释放
DestroyQueue(L);
}
}
Status Traverse(BTree t,LinkList L,int newline,int sum){
//用队列遍历输出B树
int i;
BTree p;
if(t!=NULL){
printf(" [ ");
Enqueue(L,t->ptr[0]); //入队
for(i=1;i<=t->keynum;i++){
printf(" %d ",t->key[i]);
Enqueue(L,t->ptr[i]); //子结点入队
}
sum+=t->keynum+1;
printf("]");
if(newline==0){ //需要另起一行
printf("\n");
newline=sum-1;
sum=0;
}
else
newline--;
}
if(IfEmpty(L)==FALSE){ //l不为空
Dequeue(L,p); //出队,以p返回
Traverse(p,L,newline,sum); //遍历出队结点
}
return OK;
}
Status PrintBTree(BTree t){
//输出B树
LinkList L;
if(t==NULL){
printf(" B树为空树");
return OK;
}
InitQueue(L); //初始化队列
Traverse(t,L,0,0); //利用队列输出
DestroyQueue(L); //销毁队列
return OK;
}
void Test1(){
system("color 70");
BTNode *t=NULL;
Result s; //设定查找结果
int j,n=15;
KeyType k;
KeyType a[]={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
printf("创建一棵%d阶B树:\n",m);
for(j=0;j<n;j++){ //逐一插入元素
s=SearchBTree(t,a[j]);
if(s.tag==0)
InsertBTree(t,s.i,a[j],s.pt);
printf(" 第%d步,插入元素%d:\n ",j+1,a[j]);
PrintBTree(t);
}
printf("\n");
printf("删除操作:\n"); //删除操作
k=9;
BTreeDelete(t,k);
printf(" 删除%d:\n ",k);
printf(" 删除后的B树: \n");
PrintBTree(t);
printf("\n");
k=1;
BTreeDelete(t,k);
printf(" 删除%d:\n ",k);
printf(" 删除后的B树: \n");
PrintBTree(t);
printf("\n");
printf(" 递归释放B树\n"); //递归释放B树
DestroyBTree(t);
PrintBTree(t);
}
void Test(){
int i,k;
system("color 70");
BTree t=NULL;
Result s; //设定查找结果
while(1){
printf("此时的B树:\n");
PrintBTree(t);
printf("\n");
printf("-------------Operation Table-------------\n");
printf("--- 1.Init 2.Insert 3.Delete ---\n");
printf("--- 4.Destroy 5.Exit ---\n");
printf("-----------------------------------------\n");
printf("Enter number to choose operation:\b\b\b");
scanf("%d",&i);
switch(i){
case 1:{
InitBTree(t);
printf("InitBTree successfully.\n");
break;
}
case 2:{
printf("Enter number to InsertBTree:\b\b\b");
scanf("%d",&k);
s=SearchBTree(t,k);
InsertBTree(t,s.i,k,s.pt);
printf("InsertBTree successfully.\n");
break;
}
case 3:{
printf("Enter number to DeleteBTree:\b\b\b");
scanf("%d",&k);
BTreeDelete(t,k);
printf("\n");
printf("DeleteBTree successfully.\n");
break;
}
case 4:{
DestroyBTree(t);
break;
printf("DestroyBTree successfully.\n");
}
case 5:{
exit(-1);
break;
}
}
}
}
int main(){
Test();
return 0;
}
遇到错误:Control may reach end of non-void function
解决:在指定的函数中,return语句全部在判断语句中,可能会都不执行。初步想法是改动判断语句条件,把所有情况都考虑进去;或者直接把return语句想办法拿出判断结构。
初步运行结果
已满足题目中的动态显示要求。
目前满足动态,可是很显然,需要调整一下输出,才能有树的感觉,事实上,继续使用“-|\ /”这类的符号是可行的,工作量应该是二叉平衡树的n倍,毕竟阶数的变化就是最大的变数。使用c语言时xcode使用graphics.h比较麻烦的 。
内容太多,介绍的不太详细
可以评论或者私信我,
或直接在微信小程序提问:






















 4590
4590

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










