PAT（Advanced） 1086 Tree Traversals Again（25 分）【模拟建树】

最新推荐文章于 2020-04-15 18:53:23 发布

原创最新推荐文章于 2020-04-15 18:53:23 发布 · 147 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#建树

PAT(甲级) 专栏收录该内容

55 篇文章

订阅专栏

本文介绍了一种使用栈来实现二叉树遍历的方法，并通过具体实例演示了如何根据给定的栈操作序列构建一棵唯一的二叉树，最后给出了这棵树的后序遍历序列。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

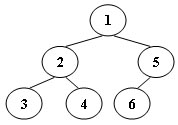
Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

解答：

该题告诉我们可以用栈的方法来实现树的建立，因此我就直接根据题意来建树。

用pre来保存插入位置的父节点，第一次插入后，给root赋值用于返回给主函数。

后序遍历我用的是递归实现。

另：我也看了其他博主的实现，他们用了先序和中序实现后序的递归操作，如果应用顺手，应该也是比较好的方法。

AC代码如下：

#include<iostream>
#include<cstdio>
#include<stack>

using namespace std;

typedef struct Node{
	int data;
	struct Node *lchild, *rchild; 
}Node, *Tree;

stack<Node*> sta;

void insertBT(Node*& root, int dir, int x)
{
	if(root == NULL)
	{
		root = new Node();
		root->data = x;
		root->lchild = root->rchild = NULL;
		sta.push(root);
	}
	else
	{
		if(dir == 'l')
			insertBT(root->lchild, dir, x);
		else 
			insertBT(root->rchild, dir, x);
	}
}

Node* buildBT(int n)
{
	Node* root = NULL, *pre = NULL;
	string action; 
	int v;
	int first = 1;

	for(int i = 0; i < 2 * n; ++i)
	{
		cin >> action;
		if(action == "Push")
		{
			cin >> v;
			if(pre == NULL || pre->lchild == NULL)
				insertBT(pre, 'l', v);
			else
				insertBT(pre, 'r', v);
			if(first == 1)
			{
				root = pre; first = 0;
			}
			pre = sta.top();
		}	
		else
		{
			pre = sta.top();
			sta.pop();
		}
	} 
	return root;
} 

int first = 1;
void postOrder(Node* root)
{
	if(root)
	{
		postOrder(root->lchild);
		postOrder(root->rchild);
		if(first == 1){
			printf("%d", root->data);	 
			first = 0;
		}else{
			printf(" %d", root->data);
		}
	}	
}

int main()
{
	int n;
	
	scanf("%d", &n);

	Node* root = buildBT(n);
	postOrder(root);
	return 0;
}