ML100天——day2

                              数据集：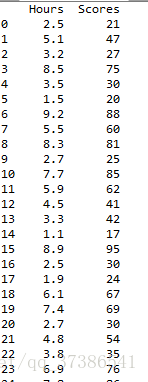                 

一.到入库及数据集 

#导入库
import pandas as pd
import numpy as np
#import matplotlib.pyplot as plt
from sklearn.cross_validation import train_test_split

#导入数据集
dataset = pd.read_csv('studentscores.csv')
X = dataset.iloc[ : , : 1].values    #自变量矩阵
Y = dataset.iloc[ : , 1].values      #因变量
 #划分数据集
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size = 1/4,random_state = 0)

                    

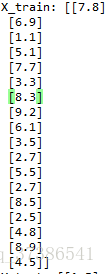
二.拟合训练集

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()     #建立regressor 对象
regressor = regressor.fit(X_train,Y_train)    #把regressor 拟合到数据集

 LinearRegression(fit_intercept=True, normalize=False,copy_X=True, n_jobs=1)

参数说明：fit_intercept——布尔型，默认为True，若参数值为True时，代表训练模型需要加一个截距项；若参数为False时，代表模型无需加截距项。

          normalize——布尔型，默认为False，若fit_intercept参数设置False时，normalize参数无需设置；若normalize设置为True时，则输入的样本数据将(X-X均值)/||X||；若设置normalize=False时，在训练模型前可以使sklearn.preprocessing.StandardScaler进行标准化处理。      

          n_jobs —— int，可选，默认1

属性： coef_：回归系数(斜率)               intercept_：截距项

主要方法：    ①fit(X, y, sample_weight=None)              ②predict(X)  利用线性模型进行预测

        ③score(X, y, sample_weight=None)，返回确定系数R ^ 2的预测。其结果等于1-(((y_true - y_pred) **2).sum() / ((y_true - y_true.mean()) ** 2).sum())，最好的分数是1.0，它可以是负数(因为模型可以任意变差)。一个常数模型总是预测y的期望值,无视输入功能,会得到一个R ^ 2得分为0.0分。

三.预测结果及可视化

#预测结果
Y_pred = regressor.predict(X_test)
#可视化
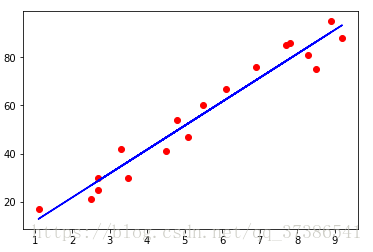
#训练集可视化
plt.scatter(X_train,Y_train,color = 'red')
plt.plot(X_train , regressor.predict(X_train),color ='blue')
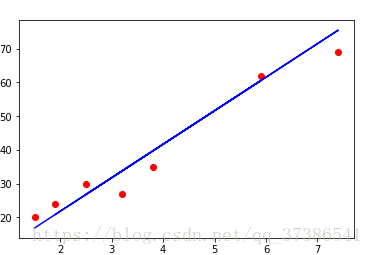
#测试集可视化
plt.scatter(X_test,Y_test,color = 'red')
plt.plot(X_test,regressor.predict(X_test),color = 'blue')
#数字化
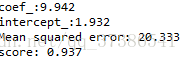
print('coef_:%.3f' % regressor.coef_)
print('intercept_:%.3f' % regressor.intercept_)
print('Mean squared error: %.3f' %((Y_test-Y_pred)**2).mean())
print('score: %.3f' % regressor.score(X_test,Y_test))