数据结构笔记（二）

最新推荐文章于 2021-08-21 20:51:16 发布

原创最新推荐文章于 2021-08-21 20:51:16 发布 · 179 阅读

CC 4.0 BY-SA版权

本文介绍了算法的基本概念，包括定义、空间复杂度S(n)和时间复杂度T(n)。讨论了好的算法标准，强调最坏情况和平均复杂度，并通过渐进表示法阐述了复杂度分析。文中还分享了算法复杂度分析的小窍门，如算法拼接和嵌套的复杂度计算。最后，给出了PAT编程题“Maximum Subsequence Sum (25)”的四种算法实现及结果对比。

基本概念——什么是算法？

一.定义

一个接受或者不需要输入的有限指令集，一定会产生输出，且在有限步骤后终止；指令的特点：有明确目标，不能有歧义；在计算机能处理的范围之内；描述应不依赖于任何一种计算机语言以及具体的实现手段

二.指标

1.空间复杂度 S（n）:根据算法写成的程序在执行时占用存储单元的长度。S(n)过高可能导致内存超限，程序非正常中断

2.时间复杂度 T（n）根据算法写成的程序在执行时耗费时间的长度。

这两者往往都与输入数据规模有关

eg1:

3.什么是好的算法？

在分析一般算法的效率时，经常关注两种复杂度：最坏情况复杂度 $T_{worst}(n)$ 和平均复杂度 $T_{avg}(n)$

$T_{worst}(n)\leqslant T_{avg}(n)$ 最坏情况复杂度比较简单，容易计算

三.复杂度的渐进表示法

1. T(n)=O(f（n）)表示存在常数C>0, $n_{0}>0$ 使得当 $n\geqslant n_{0}$ 时，有 $T(n)\leqslant C\cdot f(n)$

【简单来说对于充分大的n,O(f（n）)表示，f(n)是T（n）的某种上界】

$T(n)=\Omega (g(n))$ 表示存在常数C>0, $n_{0}>0$ ，使得当 $n\geqslant n_{0}$ 时，有 $T(n)\geqslant C\cdot g(n)$ [下界]

$T(n)=\Theta (h(n))$ 表示同时有 $T(n)=\Omega (h(n)) T(n)=O (h(n))$ ,上下界一致

tips: 通常我们尽量找出能力范围内最小的上界和最大的下界

2. 不同复杂度函数感性认识：不同函数随着n增长的增长速度

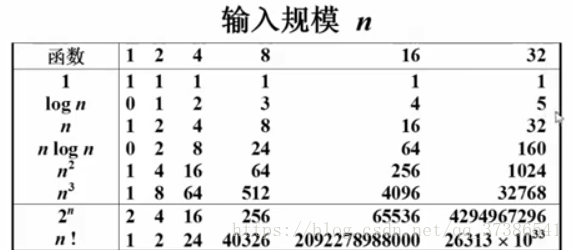
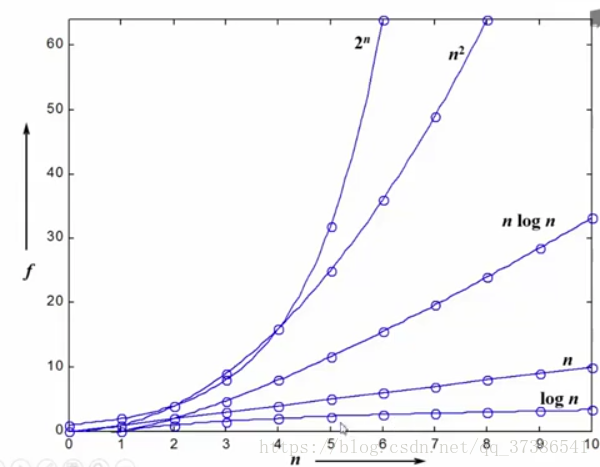
3. 复杂度分析小窍门

两段算法分别有复杂度 $T_{1}(n)=O(f_{1}(n))$ 和 $T_{2}(n)=O(f_{2}(n)$ ，则：

（1）算法拼接： $T_{1}(n)+T_{2}(n)=max(O(f_{2}(n)),O(f_{2}(n))$

(2) 算法嵌套： $T_{1}(n)\times T_{2}(n)=O(f_{1}(n)\times f_{2}(n))$

tips: 若T(n)是关于n的k阶多项式，则 $T(n)=\Theta (n^{k})$

for循环:循环次数乘以循环体代码复杂度

if-else结构：取决于if的条件判断复杂度和两个分支部分的复杂度，总体复杂度取三者最大

四.应用实例（PAT上发布的编程题实现，“Maximum Subsequence Sum (25)”是PAT(A)练习题，不仅输出最大和，而且输出相应的那个子列的首尾。）

def MaxSubseqSum1(l,N):
  start_time = time.clock()
  MaxSum = 0
  for i in range(N):
      for j in range(i,N):
          ThisSum = 0
          for k in range(i,j+1):
              ThisSum += l[k]
          if (ThisSum > MaxSum):
              MaxSum = ThisSum
  end_time = time.clock()  
  return MaxSum,end_time-start_time

算法二

def MaxSubseqSum2(l,N):
  start_time = time.clock()
  MaxSum = 0
  for i in range(N):
    ThisSum = 0
    for j in range(i,N):
      ThisSum += l[j]
      if (ThisSum > MaxSum):
        MaxSum = ThisSum
  end_time = time.clock()  
  return MaxSum,end_time-start_time

算法三

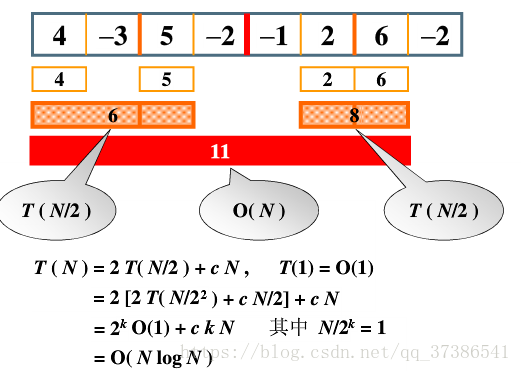
算法四：在线处理

def MaxSubseqSum3(l,N):
    start_time = time.clock()
    ThisSum = MaxSum = 0
    for i in range(N):
        ThisSum +=l[i]
        if (ThisSum > MaxSum):
            MaxSum = ThisSum
        elif(ThisSum<0):
            ThisSum = 0
    end_time = time.clock()
    return MaxSum,end_time-start_time

结果对比：