人工智能学习笔记（二）---博弈&约束满足问题&逻辑与推理

目录

一、博弈

极大极小算法

α-β剪枝

例题：

二、约束满足问题

定义：

约束传播

回溯搜索与启发式（略）

例题：

三、逻辑与推理

---

一、博弈

（a）什么是博弈问题，它和其他搜索方法比较有什么特点？

（b）提高博弈问题的搜索效率有什么方法并分析每种方法对算法最优性的影响。

 [answer]:

 （a）有完整信息的、确定的、轮流行动的、两个以上Agent的对抗搜索问题。与其他搜索算法相比，它主要的特点是多agent和更加注重实时性。

（b）提高博弈问题搜索算法效率的方法：

（1）α-β剪枝，不影响算法的最优性

（2）采用评估函数（评估当前位置的有效性）和截断测试（限制深度/时间）的方式，影响算法的最优性

（3）向前剪枝策略只考虑最优的部分分支，影响算法的最优性

（4）采用搜索表的方式，不影响算法的最优性

 

极大极小算法

max nodes：己方的选择结点，会选择评估值最大的子结点

min nodes: 对方的选择结点，会选择评估值最小的子结点

MINIMAX:所谓的极小极大值，对于MAX NODES它的值为子结点中的最大效用值，对于MIN NODES它的值为子结点中的最小效用值。

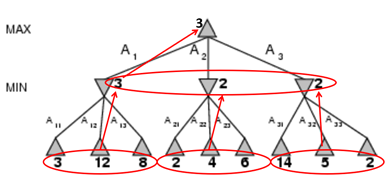
首先搜索到低层叶结点并获取其效用值，然后将极小极大值回传给上一层结点，直到值回传给根结点。

该算法对博弈树进行完整的深度优先搜索，如果树的最大深度是m，在每个结点的行棋有b个，那么时间复杂度为O(b^m)

 

α-β剪枝

α-β剪枝其实就是在极小极大搜索的基础上做了剪枝处理（没有搜索完整棵树）

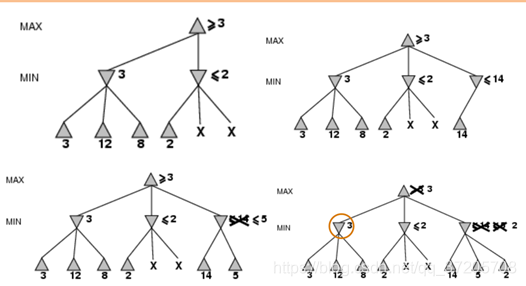
对每个结点取得的α和β

如果α<=N<=β则该结点可取，否则舍弃该结点

MAXNODE向上传递β，MINNODE向上传递α

QUESTION:这两个参数是否为全局变量，或者每个结点维护一组？---应该是每个结点自行维护

α = 到目前为止路径上发现的MAX的最佳（即极大值）选择

β = 到目前为止路径上发现的MIN的最佳（即最小值）选择

 

例题：

考虑下图的极大极小值树，搜索顺序从左到右。

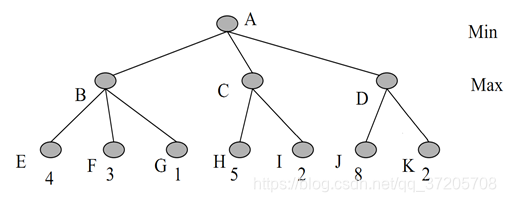
a)  根据极大极小值算法给出A结点的值并给出决策路径。

A:4； A-B-E 

b)  根据剪枝算法给出被剪枝的部分。

I, K 

c)   如果搜索顺序改为从右到左，被剪枝的部分还是一样吗？如果不是，给出被剪枝的部分。

不一样，没有结点被剪枝

d)  如果B，C，D结点都变为Chance结点，其子节点出现的概率均等，计算