这份折纸折叠代码没有考虑折痕的刚度（弹性势能和二面角有关），能否采用拉格朗日方程的方法（不要加额外的节点力）计算含折痕刚度的折纸折叠：clc
clear
close all
%% 结构参数
a=1;%四边形边长
ad=1;%虚拟点高度系数
th=60;%边夹角
h=ada;%虚拟点高度
alpha = 0.5;% 步长缩放因子
dt=0.01;%时间增量
steps=800;%步长
%%
% 定义13个节点（9实体+4虚拟）
nodes=zeros(13,3);
%实体节点（z=0,9个)
nodes(1,:) = [0, 0, 0]; % 0
nodes(2,:) = [acosd(th), asind(th), 0]; % 1
nodes(3,:) = [2acosd(th), 2asind(th), 0]; % 2
nodes(4,:) = [a, 0, 0]; % 3
nodes(5,:) = [a+acosd(th), asind(th), 0]; % 4
nodes(6,:) = [a+2acosd(th), 2asind(th), 0]; % 5
nodes(7,:) = [a+acosd(th),-asind(th), 0]; % 6
nodes(8,:) = [2a, 0 ,0]; % 7
nodes(9,:) = [2a+acosd(th), asind(th), 0]; % 8
%虚拟节点（z=h，4个）
nodes(10,:) = [(a+acosd(th))/2, asind(th)/2, h]; % 9
nodes(11,:) = [(a+acosd(th))/2+acosd(th), asind(th)/2+asind(th), h]; % 10
nodes(12,:) = [3a/2, 0, h]; % 11
nodes(13,:) = [3a/2+acosd(th),a*sind(th), h]; % 12
%%
%定义32条边（杆）
edges=[
%实体边（16）
0 1;1 2;
3 4;4 5;
6 7;7 8;
0 3;3 6;
1 4;4 7;
2 5;5 8;
1 3;3 7;2 4;4 8;
%虚拟连接(16)
0 9;1 9;3 9;4 9;
1 10;2 10;4 10;5 10;
3 11;4 11;6 11;7 11;
4 12;5 12;7 12;8 12];
%% 设定约束条件
fix = [3,21,27,9,13,14];
%构建相容性矩阵A
n_nodes = size(nodes, 1);
n_edges = size(edges, 1);
A = zeros(n_edges,3*n_nodes );
%% 可视化
figure();
colormap(jet);
free=setdiff(1:3n_nodes, fix);
%设定外部力
f=zeros(3n_nodes-size(fix,1),1);
fend=20;
for fn=0:1:fend
f(11,1)=fn;
noden = nodes; % 初始坐标
%% 循环
for step = 1:steps
% 更新A
fix1=sort(fix);
for i = 1:n_edges
j = edges(i,1)+1;% 杆件起点索引
k = edges(i,2)+1;% 杆件终点索引
vec = noden(k,:) - noden(j,:);
l= norm(vec);
lambda = vec / l; % 方向余弦向量
A(i, 3*(j-1)+1 : 3j) = -lambda;% -λ^T
A(i, 3(k-1)+1 : 3*k) = lambda;% λ^T
end
A_red = A(:, free);
% 计算零空间
[U, S, V_svd] = svd(A_red, ‘econ’);
rank_A_red=rank(A_red);
V = V_svd(:, rank_A_red+1:end); % 零空间正交基
p = size(V, 2); % 实际自由度
alpha_dot = alpha * V' * f; % 系数向量
x_dot = V * alpha_dot; % 节点速度
%% 模态选择
if step ~= 1
alpha_dot = alpha * V(:,1)’ * f; % 系数向量
x_dot = V(:,1) * alpha_dot; % 节点速度
end
dx = x_dot * dt;
dx0=dx;
for i=1:size(fix,2)
dx0=[dx0(1:fix1(i)-1,:);0;dx0(fix1(i):end,:)];
end
for i=1:n_nodes
rdx= reshape(dx0, 3, [])';
noden(i,:) = noden(i,:) + rdx(i,:);
end
%% 记录杆长误差
for i = 1:n_edges
j = edges(i,1)+1;% 杆件起点索引
k = edges(i,2)+1;% 杆件终点索引
vec_org = nodes(k,:) - nodes(j,:);
vec = noden(k,:) - noden(j,:);
l_org(i)=norm(vec_org);
l(i) = norm(vec);
end
L_vary(step) = norm(l_org-l);
nodenf=noden;
end
% 绘制边线和节点
clf;
plot3(nodenf(:,1),nodenf(:,2),nodenf(:,3),‘b*’);hold on
for i=1:n_nodes
text(nodenf(i,1)+0.05,nodenf(i,2)+0.05,nodenf(i,3)+0.05,num2str(i-1),‘Color’,‘red’) ; %加上0.01使标号和点不重合，可以调整
end
for i=1:n_edges
plot3([nodenf(edges(i,1)+1,1),nodenf(edges(i,2)+1,1)],[nodenf(edges(i,1)+1,2),nodenf(edges(i,2)+1,2)],…
[nodenf(edges(i,1)+1,3),nodenf(edges(i,2)+1,3)]);
hold on
end
% 绘制实体结构
patch_vertices = [
nodenf(1,:); nodenf(2,:); nodenf(5,:);nodenf(4,:); % 左下
nodenf(2,:); nodenf(3,:); nodenf(6,:);nodenf(5,:); % 左上
nodenf(5,:);nodenf(6,:); nodenf(9,:);nodenf(8,:); % 右上
nodenf(4,:); nodenf(5,:); nodenf(8,:);nodenf(7,:) % 右下
];
patch(‘Faces’, reshape(1:16,4,4)‘, ‘Vertices’, patch_vertices,…
‘FaceColor’,‘flat’, ‘FaceVertexCData’, linspace(0,1,16)’,…
‘EdgeColor’,‘k’, ‘LineWidth’,1.2);
% 图形设置
axis equal tight;
grid on;
% light(‘Position’,[1 1 1],‘Style’,‘infinite’);
% lighting gouraud;
% material dull;
% view(-35,25);
title(sprintf(‘4-Unit Miura-Ori Folding\nf %d/%d’,fn,fend));
xlabel(‘X’); ylabel(‘Y’); zlabel(‘Z’);
% set(gca,‘FontSize’,12,‘Projection’,‘perspective’);
set(gca,‘BoxStyle’,‘full’,‘Box’,‘on’)
set(gcf,‘Color’,[0.90 0.90 0.90])
% view(-90,0);
drawnow;
% %% 保存gif
% F=getframe(gcf);
% I=frame2im(F);
% [I,map]=rgb2ind(I,256);
%
% if step == 1
% imwrite(I,map,‘engagement_g1.gif’,‘gif’, ‘Loopcount’,inf,‘DelayTime’,0);
% else
% imwrite(I,map,‘engagement_g1.gif’,‘gif’,‘WriteMode’,‘append’,‘DelayTime’,0);
% end
end
% %% 绘制杆长误差
% figure()
% plot(L_vary)
最新发布
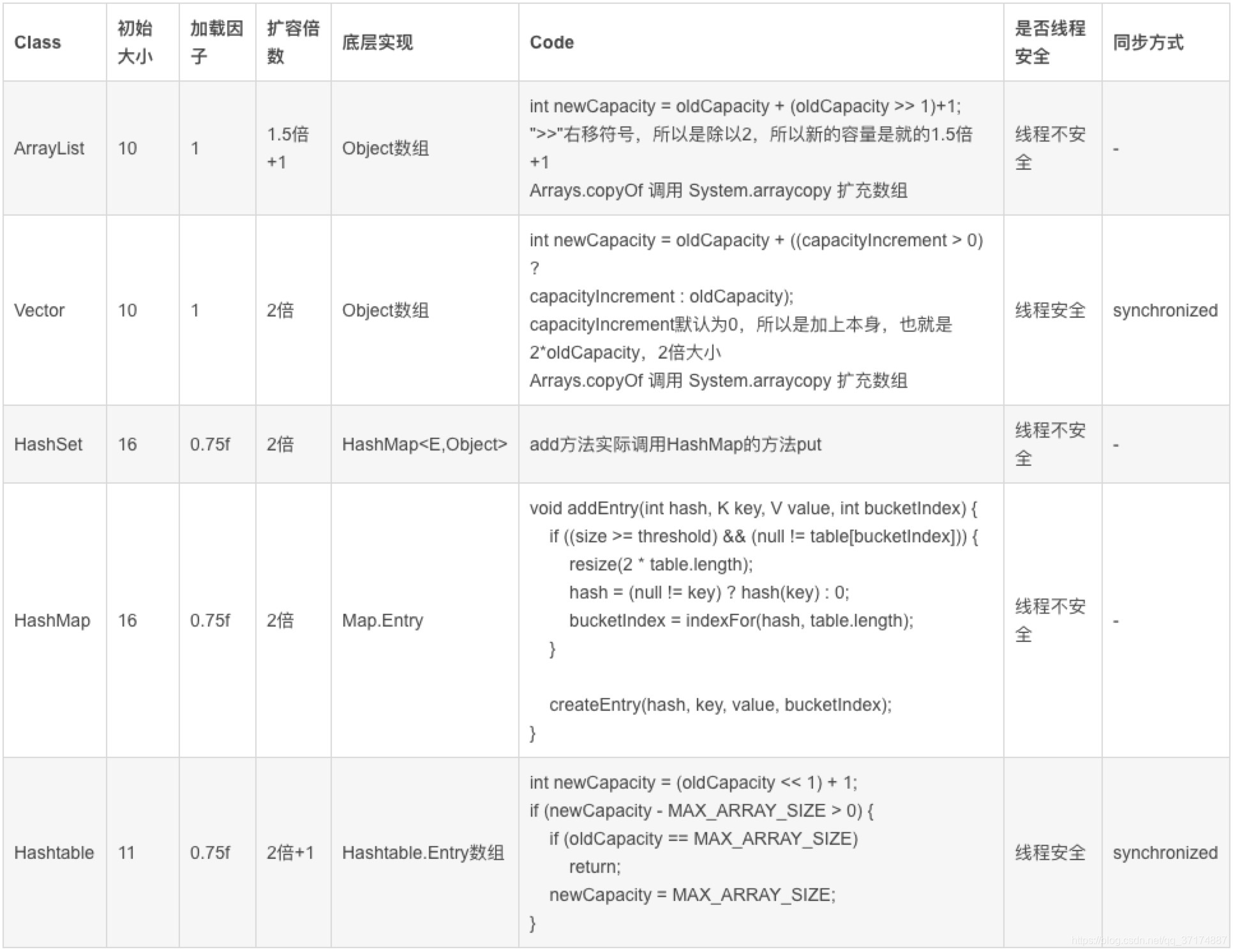
本文深入解析了Java中集合容器如List、Set、Map的初始容量、加载因子及扩容方式，对比了ArrayList、Vector、LinkedList、HashSet、HashMap、Hashtable等容器的特性与效率。
扫一扫
3376
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
