状态空间树

状态空间树：

就是问题的解空间树，分为子集树和排列树

子集树

当所给的问题是从n个元素组成的集合set中找到满足某一条件的一个子集时，相应的解空间树称为子集。
要注意，这个解空间树是一个虚拟的树，并不是构建出来的，如下面这颗树：
有三个物品n = 3，（类似于0-1背包问题）
x_i = {0、1}表示第 i 个物品 n_i 是否选中，
x_i = 0 表示未选中，x_i = 1表示选中

树有三层，第 i 层表示物品 n_i，数字1、0表示 x_i 的值

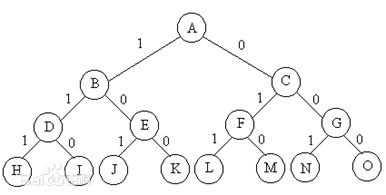
叶子上的个节点到A的路线代表了一个子集树——一种可能的解法，如 H 代表了111，表示n₁、n₂、n₃都被选中，I表示110，n₁、n₂被选中，n₃未被选中。
以下用两个例子来解释解空间树

0-1背包中使用穷举法

本文先从简单的穷举法开始介绍子集树
穷举法得到每一个子集树

• 若当前为非叶节点
  将1压栈
  递归访问左子树
  （递归访问左子树递归到最后时，例如访问到 H 时，就要pop了）
  将0压栈
  递归访问右子树
  （递归访问右子树递归到最后时，例如访问到 I 时，就要pop了）
• 若当前为叶节点
  顺序打印栈中内容

import java.util.Stack;

public class BruteForce {

	static Stack<Integer> stack = new Stack<>();

	static void subSetTree(int n) {
		if (n > 0) {
			stack.push(0);
			subSetTree(n - 1);
			stack.pop();
			stack.push(1);
			subSetTree(n - 1);
			stack.pop();
		} else {
			for (Integer integer : stack) {
				System.out.print(integer);
			}
			System.out.println();
		}
	}

	public static void main(String[] args) {
		subSetTree(3);
	}

}

排列树

TSP（Travelling Saleman Problem，货郎担、邮递员）问题、或者求全排列的问题。
以全排列为例：
定义：
设Set{S₁, S₂, S₃,…, S_n}有 n 个元素，Set_i = Set - {S_i}
子集合 X 中元素的全排列记为 arrange(X)，
(S_i)arrange(Set_i)表示在全排列arrange(Set_i)的每一个排列前加上前缀S_i得到的排列。
Set_i表示Set中没有S_i元素

Set的全排列可归纳如下：
当n=1时，arrange(Set)=(S₁)，其中S₁是集合Set中唯一的元素；
当n>1时，arrange(Set)由(S₁)arrange(Set₁)，…， (S_n)arrange(Set_n)构成。
实现思想：
将整组数中的所有的数分别与第一个数交换，这样就总是在处理后n-1个数的全排列。

有ABC三个字母，求其全排列：
当n = 3，并且Set = {a，b，c}，则：
arrange(Set)=a.arrange({b,c}) + b.arrange({a,c}) + c.arrange({a,b})
arrange({b,c})=b.arrange© + c.arrange(b)
a.arrange({b,c})=ab.arrange© + ac.arrange(b)
=ab.c + ac.b=(abc, acb)

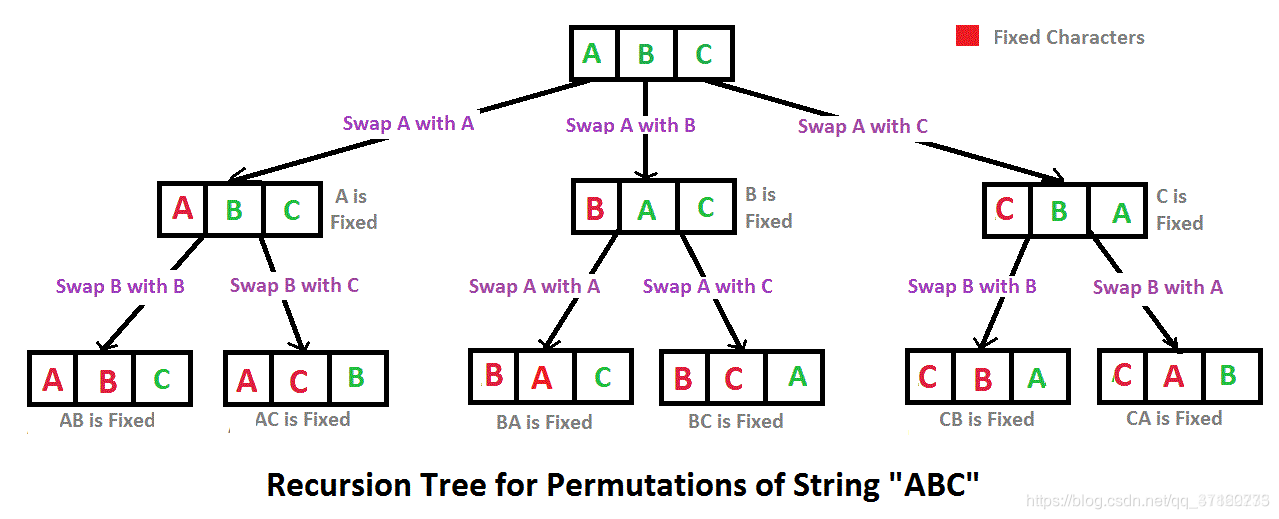
全排列

public class Tsp {
	static int[] s;

	static void arrangeTree(int i, int n) {
		// 为什么是 i < n -1。因为最后一个不用交换了
		if (i < n - 1) {
			for (int j = i; j < n; j++) {
				// swap(s[i], s[j]);
				int k = s[j];
				s[j] = s[i];
				s[i] = k;
				arrangeTree(i + 1, n);
				// 这里swap，是因为arrangeTree(i + 1, n);前的swap影响了数组 s 的顺序。
				// swap(s[i], s[j]);
				k = s[j];
				s[j] = s[i];
				s[i] = k;
			}
		} else {
			for (int j : s) {
				System.out.print(j);
			}
			System.out.println();
		}
	}

	public static void main(String[] args) {
		int n = 3;
		s = new int[n];
		for (int i = 0; i < n; i++) {
			s[i] = i + 1;
		}
		arrangeTree(0, n);
	}

}

emmmm，全排列这个其实挺迷的

总结

• 递归简单，但如何将问题分解成递归就不容易了
• 递归的判出界限让人很迷