机器学习实战——6.支持向量机_请计算这6个数据采样的最大间隔分离平面,并指出相应的支持向量-优快云博客

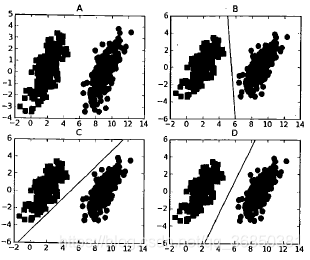
如上图所示：当两组数据分隔的足够开，很容易就可以在图上画出一条直线将两组数据点分开时，这组数据被称为线性可分数据，将数据集分隔开来的直线称为分隔超平面。数据点都在二维平面上时，分隔超平面就只是一条直线；数据集是三维时，用来分隔数据的就是一个平面；更高维的就叫超平面，也就是分类的决策边界。分布在超平面一侧的所有数据都属于某个类别，而分布在另一侧的所有数据则属于另一个类别。

我们希望采用这种方式来构建分类器，即如果数据点离决策边界越远，那么其最后的预测结果也就越可信。考虑上图B、C、D中的三条直线，它们都能将数据分隔开，但是其中哪一条最好呢？我们采用的是找到离分隔超平面最近的点，确保它们离分隔面的距离尽可能远。这里点到分隔面的距离被称为间隔。我们希望间隔尽可能大，这是因为如果我们犯错或者在有限数据上训练分类器的话，我们希望分类器尽可能健壮。

支持向量就是离分隔超平面最近的那些点，接下来要试着最大化支持向量到分隔面的距离，需要找到此问题的优化求解方法。

6.2 寻找最大间隔

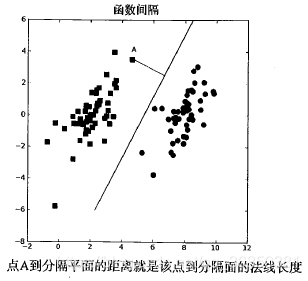
如何求解数据集的最佳分隔直线？先来看下图，分隔超平面的形式可以写成 $\omega ^{T}x+b$ 。要计算点A到分隔超平面的距离，就必须给出点到分隔面的法线或垂线的长度，该值为 $\left | \omega ^{A+b} \right |/\left \| \omega \right \|$ 。这里的常数b类似于Logistic回归中的截距 $\omega _{0}$ 。这里的向量w和常数b一起描述了所给数据的分隔线或超平面。接下来讨论分类器。

6.2.1 分类器求解的优化问题

输入数据给分类器会输出一个类别标签，这相当于一个类似于Sigmoid的函数在作用。下面将使用海维赛德阶跃函数（即单位阶跃）的函数对 $\omega ^{T}x+b$ 作用得到 $f(\omega ^{T}x+b)$ ，其中当u<0时，f(u)输出-1，反之则输出+1.这和Logistic回归有所不同，那里的类别标签是0或1。

这里的类别标签为什么采用-1和+1，而不是0和1呢？这是由于-1和+1仅仅相差一个符号，方便数学上的处理。我们可以通过一个统一公式来表示间隔或者数据点到分隔超平面的距离，同时不必担心数据到底是属于-1还是+1类。

当计算数据点到分隔面的距离并确定分隔面的放置位置时，间隔通过 $label*(\omega ^{T}x+b)$ 来计算，这时就能体现出-1和+1类的好处了。如果数据点处于正方向（即+1类）并且离分隔超平面很远的位置时， $\omega ^{T}x+b$ 会是一个很大的正数，同时 $label*(\omega ^{T}x+b)$ 也会是一个很大的正数。而如果数据点处于负方向（-1类）并且离分隔超平面很远的位置时，此时由于类别标签为-1，则 $label*(\omega ^{T}x+b)$ 仍然是一个很大的正数。

现在的目标就是找出分类器定义中的w和b。为此，我们必须找到具有最小间隔的数据点，而这些数据点也就是前面提到的支持向量。一旦找到具有最小间隔的数据点，我们就需要对该间隔最大化。这就可以写作：

$argmax\left \{ min\left ( label(w^{T}+b))\frac{1}{\left \| w \right \|} \right ) \right \}$

直接求解上述问题相当困难，所以我们将它转换成为另一种更容易求解的形式。首先考察一下上式中大括号内的部分。由于对乘积进行优化是一件很讨厌的事情，因此我们要做的是固定其中一个因子而最大化其它因子。如果令所有支持向量的 $label*(\omega ^{T}x+b)$ 都为1，那么就可以通过求 $\left \| w \right \|^{-1}$ 的最大值来得到最终解。但是并非所有数据点的 $label*(\omega ^{T}x+b)$ 都等于1，只有那些离分隔超平面最近的点得到的值采为1.而离超平面越远的数据点，其 $label*(\omega ^{T}x+b)$ 的值也就越大。

在上述优化问题中，给定了一些约束条件然后求最优值，因此该问题是一个带约束条件的优化问题。这里的约束条件就是 $label*(\omega ^{T}x+b)\geqslant 1$ 。对于这类优化问题，有一个非常著名的求解方法，即拉格朗日乘子法。通过引入拉格朗日乘子，我们就可以基于约束条件来表述原来的问题。由于这里的约束条件都是基于数据点的，因此我们就可以将超平面写成数据点的形式，于是优化目标函数最后可以写成：

$max[\sum_{i=1}^{m}\alpha -\frac{1}{2}\sum_{i,j=1}^{m}label^{(i)}label^{(j) }a_{i}a_{j}\left \langle x^{(i)},x^{(j)} \right \rangle]$

其约束条件为：

$\alpha \geqslant 0,\sum_{i=1}^{m}\alpha _{i}label^{(j)}=0$

以上的描述都是基于一个假设：数据必须100%线性可分。但是几乎所有数据都不是完全线性可分的，这时就可以通过引入所谓松弛变量，来允许有些数据点可以处于分隔面的错误一侧。这样我们的优化目标就能保持仍然不变，但是此时新的约束条件则变为：

$C\geqslant \alpha \geqslant 0,\sum_{i=1}^{m}\alpha _{i}label^{(j)}=0$

这里的常数C用于控制“最大化间隔”和“保证大部分点的函数间隔小于1.0”这两个目标的权重。在优化算法的实现代码中，常数C是一个参数，因此可以通过调节该参数得到不同的结果。一旦求出了所有的alpha，那么分隔超平面就可以通过这些alpha来表达。这一结论十分直接，SVM的主要工作是求解这些alpha。

6.2.2 SVM应用的一般框架

SVM的一般流程：

（1）收集数据：可以使用任意方法。

（2）准备数据：需要数值型数据。

（3）分析数据：有助于可视化分隔超平面。

（4）训练算法：SVM的大部分时间都源自训练，该过程主要实现两个参数的调优。

（5）测试算法：十分简单的计算过程就可以实现。

（6）使用算法：几乎所有分类问题都可以使用SVM，值得一提的是，SVM本身是一个二分类器，对多分类问题应用SVM需要对代码做一些修改。

6.3 SMO高效优化算法

以前人们使用二次规划求解工具求解最优化问题，这种工具是一种用于在线性约束下优化具有多个变量的二次目标函数的软件。而这些二次规划求解工具则需要强大的计算能力支撑，另外在实现上也十分复杂。所有需要做的围绕优化的事情就是训练分类器，一旦得到alpha的最优值，我们就得到了分隔超平面并能够将之用于数据分类。

6.3.1 Platt的SMO算法

1996年，JohnPlatt发布了一个称为SMO的强大算法，用于训练SVM。SMO表示序列最小优化。Platt的SMO算法是将大优化问题分解为多个小优化问题来求解的。这些小优化问题往往很容易求解，并且对他们进行序列求解的结果将它们作为整体来求解的结果是完全一致的。在结果完全相同的同时，SMO算法的求解时间短很多。

SMO算法的目标是求出一系列alpha和b，一旦求出了这些alpha，就很容易计算出权重向量w并得到分隔超平面。

SMO算法的工作原理是：每次循环中选择两个alpha进行优化处理。一旦