决策粗糙集

写在前面

粗糙集介绍

决策粗糙集

---

1 决策粗糙集的引入

粗糙集的的思想：使用可定义集合刻画不可定义集合，从而给出上下近似集的概念定义。

Pawlaw经典粗糙集，只考虑了 定性 关系，过于严格、容错能力不足.

决策粗糙集模型：结合概率论展开研究，给出了粗糙集理论的 定量 描述。

定性：决定其概念、性质，只决定其含义。
定量：在定性的基础之上进行量化，定性过程中量的边界。

---

2. Pawlaw经典粗糙集回顾

粗糙集理论首次形式化地描述了对象的不可分辨性、属性冗余性及属性约简等重要概念。

重要贡献： 给出一种基于等价关系的数据分析方法，并且给出了一个非常精确、严格的数学描述。

上近似： a p r ‾ ( X ) = { x ∈ U ∣ [ x ] ∩ X ≠ ∅ } \overline{apr}(X) = \{x\in U | [ x] \cap X \neq \empty\} apr​(X)={x∈U∣[x]∩X̸​=∅}
下近似： a p r ‾ ( X ) = { x ∈ U ∣ [ x ] ⊆ X } \underline{apr}(X) = \{x\in U | [ x] \subseteq X \} apr​(X)={x∈U∣[x]⊆X}
正域（必然性）： P O S ( X ) = a p r ‾ ( X ) = { x ∈ U ∣ [ x ] ⊆ X } POS(X) = \underline{apr}(X) = \{x\in U | [ x] \subseteq X \} POS(X)=apr​(X)={x∈U∣[x]⊆X}
负域： N E G ( X ) = U − a p r ‾ ( X ) = { x ∈ U ∣ [ x ] ∩ X = ∅ } NEG(X) =U - \overline{apr}(X) = \{x\in U | [ x] \cap X = \empty\} NEG(X)=U−apr​(X)={x∈U∣[x]∩X=∅}
边界域（可能性）： B N D ( X ) = a p r ‾ ( X ) − a p r ‾ ( X ) = { x ∈ U ∣ [ x ] ∩ X ≠ ∅ ∧ ¬ ( [ x ] ⊆ X ) } BND(X) =\overline{apr}(X) - \underline{apr}(X) = \{x\in U | [ x] \cap X \neq \empty \wedge \lnot ([x] \subseteq X)\} BND(X)=apr​(X)−apr​(X)={x∈U∣[x]∩X̸​=∅∧¬([x]⊆X)}

---

3. 决策粗糙集

3.1 问题引入

---

Pawlaw经典粗糙集被看作一种定性的近似，其定义不允许任何不确定性，这是优点也是缺点。

不允许任何的不确定性，难以体现概念表示的 容错性（包含错误的能力：宰相的肚子）。

由以上原因，考虑另外一种粗糙集的表示，将概念近似空间引入到粗糙集研究中，即：概率粗糙集模型。

1987年Wong和Xiarko将概率近似空间引入到粗糙集研究中。

3.2 基本理论

---

$Pr(X|[x])$表示 任何一个属于[x]的对象 属于X的 条件概率，属于[x]是条件。

可获得以下等价条件：

	条件	表示
POS	$$Pr(X/[x])=1\iff [x]\subseteq X$$	{ x ∈ U ∥ { P r ( X / [ x ] ) = 1 } \{x \in U \| \{ Pr(X/[x])=1\} {x∈U∥{Pr(X/[x])=1}
NEG	$$Pr(X/[x])=0\iff [x]\cap X=\varnothing$$	{ x ∈ U ∥ { P r ( X / [ x ] ) = 0 } \{x \in U \| \{ Pr(X/[x])=0\} {x∈U∥{Pr(X/[x])=0}
BND	$$0<Pr(X/[x])<1\iff [x]\cap X̸=\varnothing \wedge \neg ([x]\subseteq X)\}$$	{ x ∈ U ∥ { 0 &lt; P r ( X / [ x ] ) &lt; 1 } \{x \in U \| \{ 0&lt; Pr(X/[x])&lt;1\} {x∈U∥{0<Pr(X/[x])<1}

上述的 0 和 1 是概率的两个极端值，我们可以使用其他（0 < t < 1）的值来表示。

我们使用 $\beta$ 和 $\alpha$ 来替换上述的 0 , 1 值的时候就是 决策粗糙集。0< $\beta$ < $\alpha$ < 1。

	条件
POS	P O S ( α , β ) = { x ∈ U ∥ { P r ( X / [ x ] ) ≥ α } POS_{(\alpha ,\beta)} = \{x \in U \| \{ Pr(X/[x]) \ge \alpha \} POS(α,β)​={x∈U∥{Pr(X/[x])≥α}
NEG	N E G ( α , β ) = { x ∈ U ∥ { P r ( X / [ x ] ) ≤ β } NEG_{(\alpha ,\beta)} = \{x \in U \| \{ Pr(X/[x]) \leq \beta\} NEG(α,β)​={x∈U∥{Pr(X/[x])≤β}
BND	B N D ( α , β ) = { x ∈ U ∥ { β &lt; P r ( X / [ x ] ) &lt; α } BND_{(\alpha ,\beta)} =\{x \in U \| \{ \beta&lt; Pr(X/[x])&lt;\alpha\} BND(α,β)​={x∈U∥{β<Pr(X/[x])<α}

当$(\beta ,\alpha )$为（0,1）时候，决策粗糙集就成为了经典粗糙集。

3.3 待解决的问题

---

1. 阈值$\beta$ 和 $\alpha$ 的解释和计算。（贝叶斯决策论处理）
2. 条件概率$Pr(X/[x])$的估计。（朴素贝叶斯）
3. 概率正、负和边界域的解释和应用。（三支决策）

---

4. 问题处理

---

4.1 阈值$\beta$ 和 $\alpha$ 的解释和计算（贝叶斯决策论处理）

---

研究 将对象划分到对应域的损失 来解释和计算阈值。

损失函数 ：

$a_P，a_N，a_B$：分别为将对象分类到正域、负域和边界域的决策动作。
${\lambda }_{PP}，{\lambda }_{NP}，{\lambda }_{BP}$：表示一个对象 属于 集合X时候采取$a_P，a_N，a_B$决策带来的损失函数
${\lambda }_{PN}，{\lambda }_{NN}，{\lambda }_{BN}$：表示一个对象 不属于 集合X时候采取$a_P，a_N，a_B$决策带来的损失函数

对于[x]中对象不同动作产生的 损失表示 ：

划分到正域：
$$（1）R(a_P|[x])={\lambda }_{PP}\ast Pr(X|[x])+{\lambda }_{PN}\ast Pr(X^c|[x])$$
划分到边界域：
$$（2）R(a_B|[x])={\lambda }_{BP}\ast Pr(X|[x])+{\lambda }_{BN}\ast Pr(X^c|[x])$$
划分到负域：
$$（3）R(a_N|[x])={\lambda }_{NP}\ast Pr(X|[x])+{\lambda }_{NN}\ast Pr(X^c|[x])$$

（Note：$X^c$是$X$的补集）

最小风险决策规则 ：

若（1）<= （2） 且（1）<= （3）则：$x\in POS(X)$
若（2）<= （1） 且（2）<= （3）则：$x\in BND(X)$
若（3）<= （1） 且（3）<= （2）则：$x\in NEG(X)$

$\beta$、 $\alpha$ 和 $\lambda$ 的产生

由于以下公式：$$Pr(X|[x])+\ast Pr(X^c|[x])=1$$
Note：$X^c$是$X$的补集。
我们可以使用 损失函数$\lambda$ 和 $Pr(X|[x])$ 简化 最小风险决策规则。

一般来说一个属于X的对象x划分到三个域的损失有以下情况：
$${\lambda }_{PP}<={\lambda }_{BP}<{\lambda }_{NP}$$

$${\lambda }_{NN}<={\lambda }_{BN}<{\lambda }_{PN}$$
基于以上条件可得到3个阈值：
$$\alpha =\frac{{\lambda }_{PN}-{\lambda }_{BN}}{({\lambda }_{PN}-{\lambda }_{BN})+({\lambda }_{BP}-{\lambda }_{PP})}$$

$$\lambda =\frac{{\lambda }_{PN}-{\lambda }_{NN}}{({\lambda }_{PN}-{\lambda }_{NN})+({\lambda }_{NP}-{\lambda }_{PP})}$$

$$\beta =\frac{{\lambda }_{BN}-{\lambda }_{NN}}{({\lambda }_{BN}-{\lambda }_{NN})+({\lambda }_{NP}-{\lambda }_{BP})}$$

最小风险决策规则2(使用alpha、beta 和 lambda)：

若 $Pr(X|[x])\ge \alpha$ 且 $Pr(X|[x])\ge \lambda$ 则 ：$x\in POS(X)$
若 $Pr(X|[x])\le \alpha$ 且 $Pr(X|[x])\ge \beta$ 则 ：$x\in BND(X)$
若 $Pr(X|[x])\le \beta$ 且 $Pr(X|[x])\le \lambda$ 则 ：$x\in NEG(X)$

最小风险决策规则3（去除lambda）：

进一步假设 $\frac{{\lambda }_{NP}-{\lambda }_{BP}}{{\lambda }_{NP}-{\lambda }_{NN}}>\frac{{\lambda }_{BP}-{\lambda }_{PP}}{{\lambda }_{PN}-{\lambda }_{BN}}$ ,可证明 $\alpha$ > $\lambda$ > $\beta$，则不再需要阈值 $\lambda$ ，风险决策可简化。

若 $Pr(X|[x])\ge \alpha$ 则 ：$x\in POS(X)$
若 $\beta <Pr(X|[x])<\alpha$ 则 ：$x\in BND(X)$
若 $Pr(X|[x])\le \beta$ 则 ：$x\in NEG(X)$

4.2 条件概率$Pr(X/[x])$的估计（朴素贝叶斯）

---

使用朴素贝叶斯公式对条件概率$Pr(X/[x])$进行估计。

朴素贝叶斯公式：

$$Pr(X|[x])=\frac{Pr([x]|X)Pr(X)}{Pr([x])}（公式1）$$

$Pr(X|[x])$：后验概率
$Pr([x]|X)$：似然函数
$Pr(X)$：先验概率

后验概率 转化为 似然比

通过引入赔率(odds)变换、对数(logit)变换将$Pr(X|[x])$转换为
$$\frac{Pr([x]|X)}{Pr([x]|X^c)}$$
即：
$$logit(Pr([x]|X))=log(O(Pr([x]|X)))=log(\frac{Pr([x]|X)}{Pr([x]|X^c)})+log(\frac{Pr(X)}{Pr(X^c)})（公式2）$$

对象子集 $[x]$ 使用属性子集 $A\subseteq At$ ： [ x ] = [ x ] A = ∩ a ∈ A [ x ] { a } [x] = [x]_A = \cap_{a\in A}[x]_{\{a\}} [x]=[x]A​=∩a∈A​[x]{a}​。

估计$Pr([x]|X)$和$Pr([x]|X^c)$

为了估计$Pr([x]|X)$和$Pr([x]|X^c)$，做出如下假设：

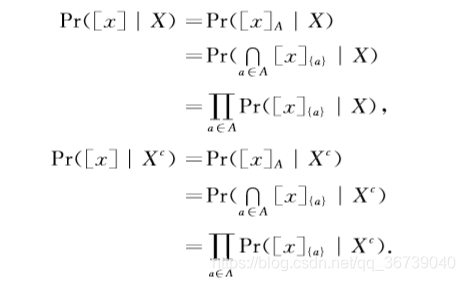
代入公式2：

阈值来说建立以下关系：

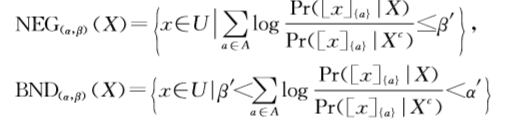
4.3 概率正、负和边界域的解释和应用（三支决策）

---

粗糙集可以看作是三支决策的特例，三支决策给出了更加广泛的理论、方法和工具。

5 定性定量区别

定性：不容许错误。
定量：可以容忍错误。

现实生活中不存在绝对的错误，所以定量的方式更有意义。

详细了解请查阅论文：决策粗糙集理论研究现状与展望