WIKI
In machine learning, support vector machines (SVMs, also support vector networks[1]) are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis.
-
支持向量机是一种二类分类模型
-
间隔最大使它有别于感知机
-
支持向量机还包括核技巧,这使它成为实质上的非线性分类器
-
支持向量机的学习算法是求解凸二次规划的最优化算法
|
训练数据 |
通过 |
学习 |
称为 |
|
线性可分 |
硬间隔最大化 |
线性的分类器 |
线性可分/硬间隔支持向量机 |
|
近似线性可分 |
软间隔最大化 |
线性的分类器 |
线性/软间隔支持向量机 |
|
线性不可分 |
核技巧及软间隔最大化 |
|
非线性支持向量机 |
线性可分支持向量机与硬间隔最大化
线性可分支持向量机
-
输入都是由输入空间转换到特征空间,支持向量机的学习是在特征空间进行的
-
学习的目标是在特征空间中找到一个分离超平面,能将实例分到不同的类
-
感知机利用误分类最小的策略,解是无穷的;线性可分支持向量机利用间隔最大化策略,解是唯一的

函数间隔和几何间隔
函数间隔

几何间隔

函数间隔和几何间隔
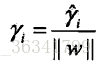
间隔最大化
-
支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面
-
间隔最大化的直观解释是:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类

学习的对偶算法


线性支持向量机与软间隔最大化
线性支持向量机

学习的对偶算法

支持向量
软间隔的支持向量
-
间隔边界上
-
间隔边界与分离超平面之间
-
分离超平面误分的一侧
合页损失函数
线性支持向量机学习还有另外一种解释,就是最小化以下目标函数:
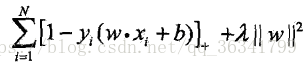
-
目标函数第一项是经验损失或经验风险
-
目标函数第二项是系数为λ的w的L2范数
非线性支持向量机与核函数
核技巧
用线性分类方法求解非线性分类问题分两步:
-
首先使用一个变换将原空间的数据映射到新空间
-
然后在新空间里用线性分类学习方法从训练数据中学习分类模型
![]()

正定核
通常所说的核函数就是正定核函数
常用核函数

非线性支持向量分类机
非线性支持向量机学习算法

序列最小最优化算法
SMO算法要解如下凸二次规划的对偶问题
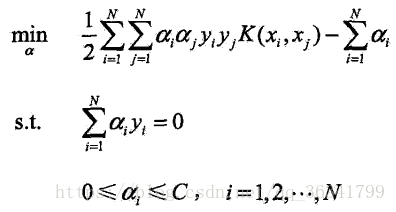
-
SMO算法是一种启发式算法
-
基本思想:如果所有变量的解都满足此最优化问题的KKT条件,那么这个最优化问题的解就得到了
-
KKT条件是该最优化问题的充要条件
-
SMO算法将原问题不断分解为子问题求解,进而达到求解原问题的目的
-
整个SMO算法包括:①求解两个变量二次规划的解析方法②选择变量的启发式方法
SMO算法

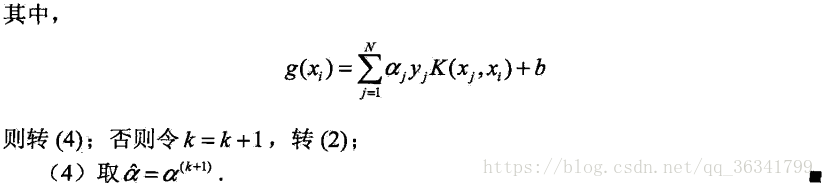





 本文深入探讨了支持向量机(SVM)的概念及其在机器学习中的应用。SVM是一种用于分类和回归分析的监督学习模型,特别介绍了其通过间隔最大化策略实现独特分类效果的原理,以及如何使用核技巧处理非线性分类问题。
本文深入探讨了支持向量机(SVM)的概念及其在机器学习中的应用。SVM是一种用于分类和回归分析的监督学习模型,特别介绍了其通过间隔最大化策略实现独特分类效果的原理,以及如何使用核技巧处理非线性分类问题。
















 4138
4138

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








