刷题不在于多,在于精,了解每一道题目背后所包含的思想,并掌握其精髓,即可举一反三,达到事半功倍的效果,现在继续跟着小曾开启刷题之旅!
文章目录
对于链表,指两个变量在链表上同向移动解决的问题–【快慢指针】问题

【主要针对的数据结构存储方式是 链表 、链表 、链表】
快慢指针⼀般都初始化指向链表的头结点 head,前进时快指针 fast 在前,慢指针 slow 在后,巧妙解决⼀些链表中的问题。
下面主要分为四种问题,现在来一一解析:
1、判定链表中是否含有环
这是遇到题目的首要判断操作,也是最基本的操作。
单链表主要特点:head = head.next ,只知道下一个节点,但是无法判断是否含有环。
如果一个链表不含环,那么指针指向空指针null 就结束了。
boolean hasCycle(ListNode head) {
while(head!=null)
head=head.next;
return false;
}
那么,如果链表中含有环,指针如果直接下一个节点,就会陷入死循环,因此在环形链表中并没有null来进行终结。
解决方案:就是用两个指针,⼀个跑得快,⼀个跑得慢。如果不含有环,跑得快的那个指针最终会遇到 null,说明链表不含环;如果含有环,快指针最终会超慢指针⼀圈,和慢指针相遇,说明链表含有环。
判断是否有环的代码模板
boolean hasCycle(ListNode head){
ListNode fast ,slow ;
fast = slow = head ;
while (fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
if(fast == slow) return true;
}
例如141题,环形链表
2、已知链表中含有环,返回这个环的起始位置
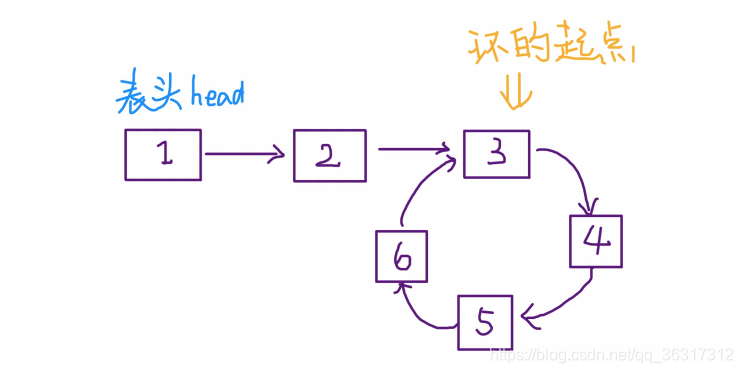
当快慢指针相遇时,让其中任⼀个指针指向头节点,然后让它俩以相同速度前进,再次相遇时所在的节点位置就是环开始的位置。这是为什么呢?
第⼀次相遇时,假设慢指针 slow ⾛了 k 步,那么快指针 fast ⼀定⾛了 2k步,也就是说⽐ slow 多⾛了 k 步(也就是环的⻓度)
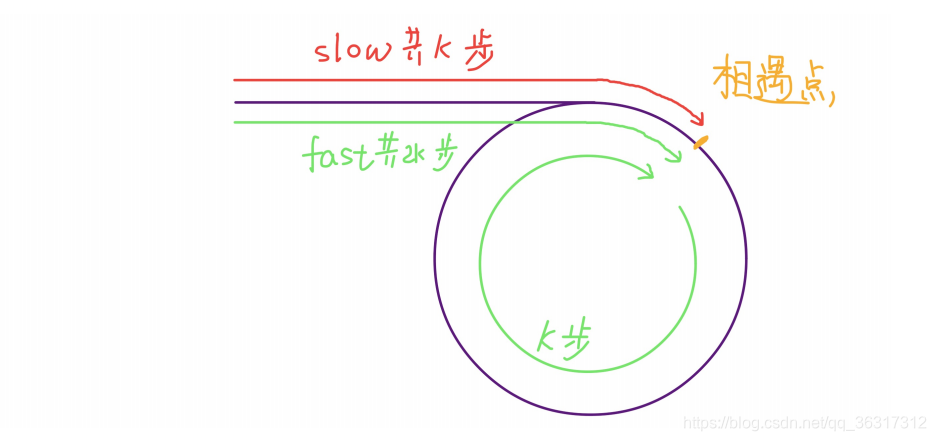
设相遇点距环的起点的距离为 m,那么环的起点距头结点 head 的距离为 k -m,也就是说如果从 head 前进 k - m 步就能到达环起点。巧的是,如果从相遇点继续前进 k - m 步,也恰好到达环起点。
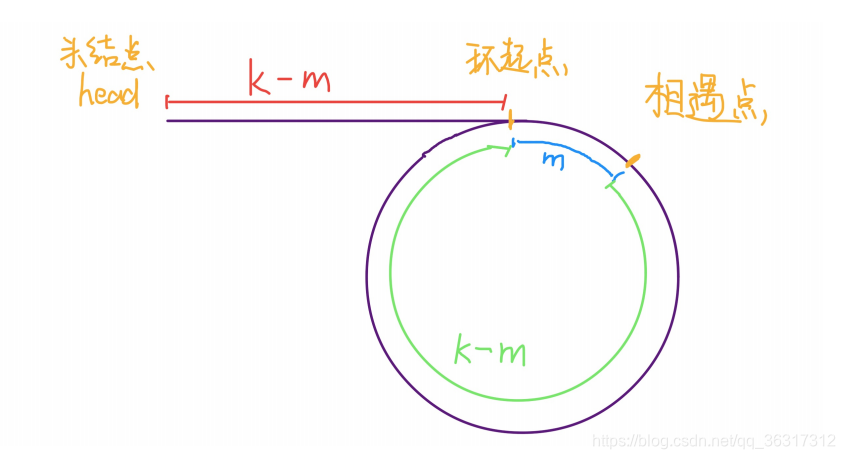
所以,只要我们把快慢指针中的任⼀个重新指向head,然后两个指针同速前进,k - m 步后就会相遇,相遇之处就是环的起点了。
ListNode detectCycle(ListNode head){
ListNode fast,slow;
fast=slow=head;
while(fast !=null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast==slow) break;
}
slow = head;
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
具体题目如 142 环形链表II
3、寻找链表的中点
思路:可以让快指针一次前进两步,慢指针一次前进一步,当快指针到达链表尽头的时候,这个时候慢指针就处于链表中点的位置
对于快慢指针而言,掌握思想最重要,对于很多题目换汤不换药,精髓掌握,以不变来应万变!
while(fast != null && fast.next){
fast = fast.next.next
slow = slow.next
}
#链表长度为奇数,slow恰好停在中点位置;长度为偶数,slow最终是中间偏右
return slow
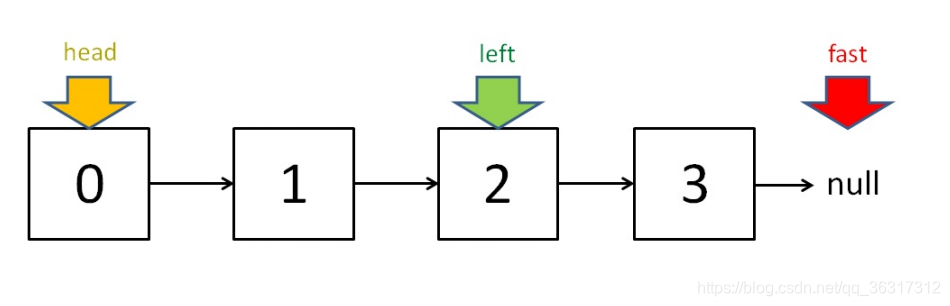
为什么要寻找链表中点?
对链表进行归并排序,同时可以对排序的链表进行二分查找等操作。
4、寻找倒数k个元素
思路:使用快慢指针,让快指针先走k步,然后开始快慢指针同速前进,当快指针⾛到链表末尾 null 时,慢指针所在的位置就是倒数第 k个链表节点。
这个在下面有具体介绍,可以看下面19题目的详细解答。
leetcode部分题目
19、删除链表的倒数第N个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
**要求:**你能尝试使用一趟扫描实现吗? 双指针中的快慢指针
示例:
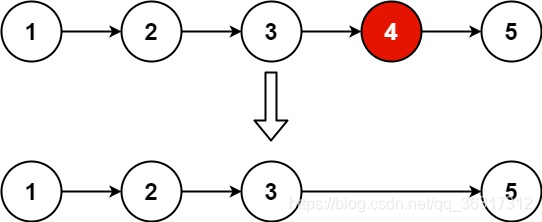
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
**题目分析:**首先找到倒数第N个节点,然后再进行删除操作
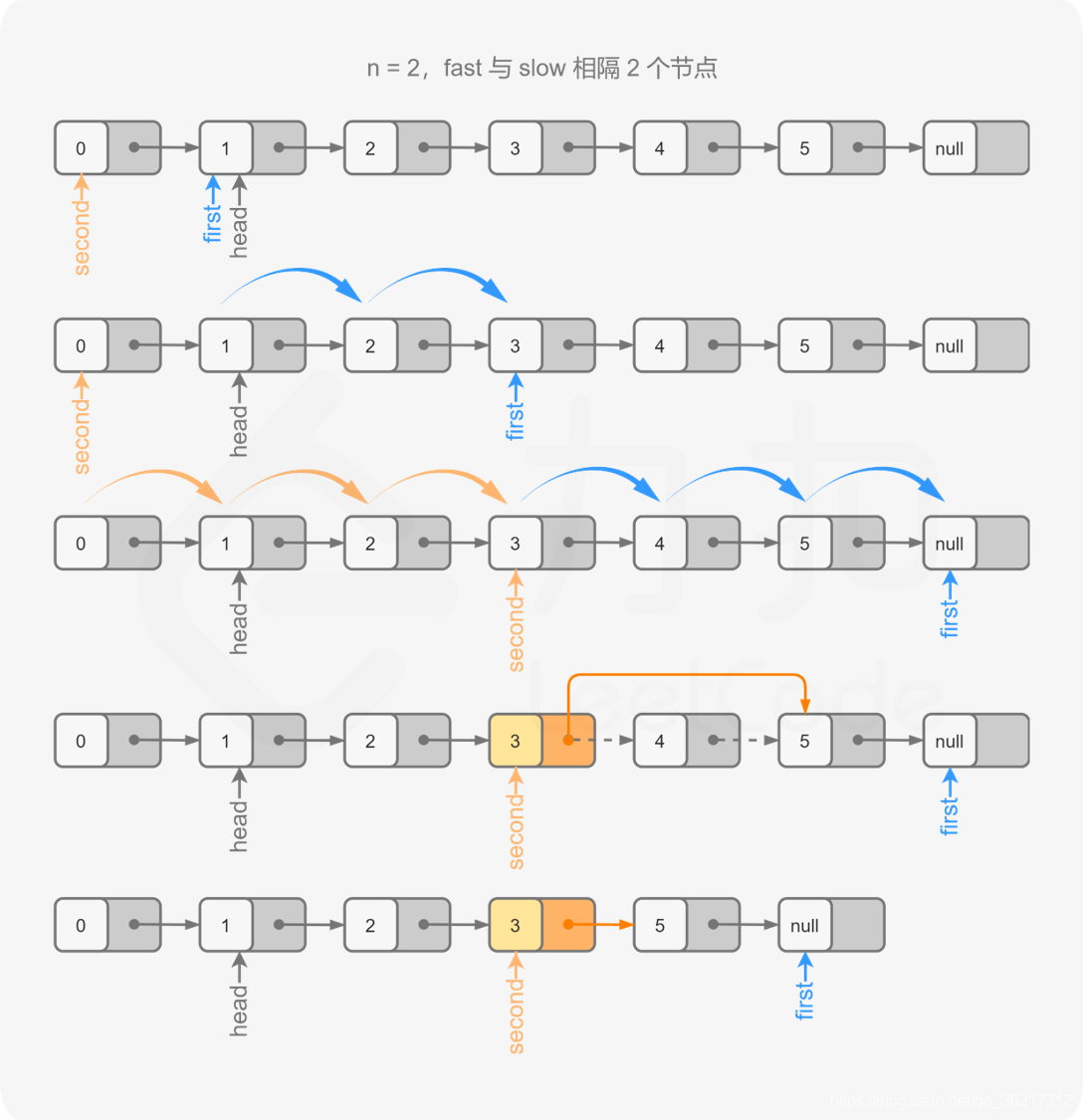
**具体思路:**采用快慢指针思路,设置两个指针first,second,同时对链表进行遍历,并且指针first比指针second超前N个节点,这样当first遍历完后,second所对应的就是第N个节点。
具体步骤:
1、初始化时候,first 和second 都指向头节点,然后first开始进行遍历N次,这样的话first - second = n (first超前second n 个节点)
【在进行链表删除操作的时候,知道倒数第n个节点的前驱节点是最好的,可以在second指向哑节点,second.next 是删除节点】
2、first 和second 开始对链表进行遍历,当 first 遍历到链表的末尾,first 为空指针时,second 恰好指向倒数第 n 个节点。
python 版本
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
#初始化
head_Node = ListNode(0 , head)
first = head
second = head_Node
#开始移动first 和second
for i in range(n):
first = first.next
#判断 first指针不为空,继续遍历
while first:
first = first.next
second = second.next
#删除操作
second.next = second.next.next
return head_Node.next
java版本,具体思路是一致的,写法有些许不同
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode head_node = new ListNode(0,head);
ListNode first = head;
ListNode second = head_node;
for(int i=0;i<n;i++){
first = first.next;
}
while(first != null) {
first = first.next;
second = second.next;
}
second.next = second.next.next;
return head_node.next;
}
}
61、旋转链表
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
示例1:
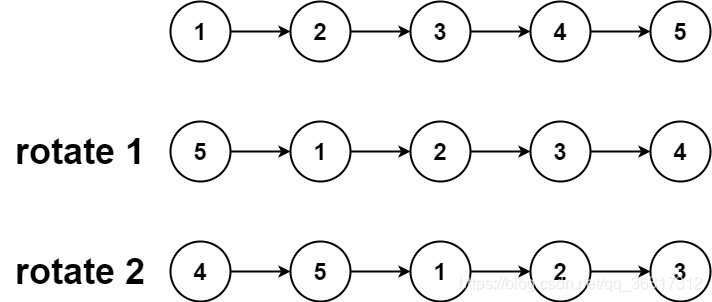
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
示例2:
**具体思路:**跟19题目比较类似,19题目主要找到倒数第k个节点并删除,而现在主要是找到倒数第k个节点,然后将快指针所指的后继指针指向链表头节点,使链表成环。
具体步骤:
1、定义慢指针slow和快指针fast,其初始都指向链表头节点
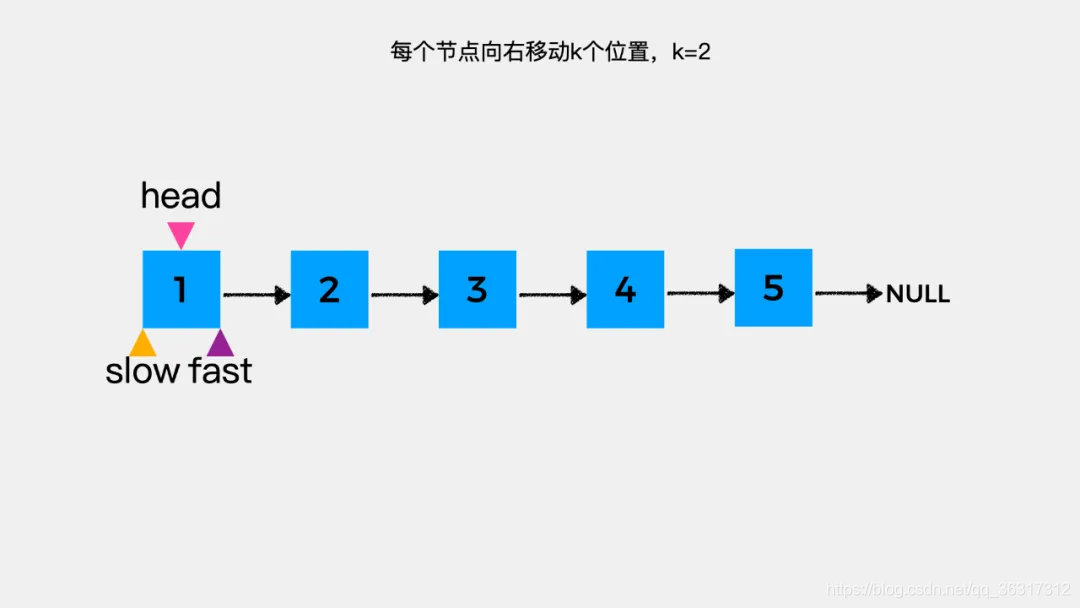
2、让快指针fast先向前移动2步
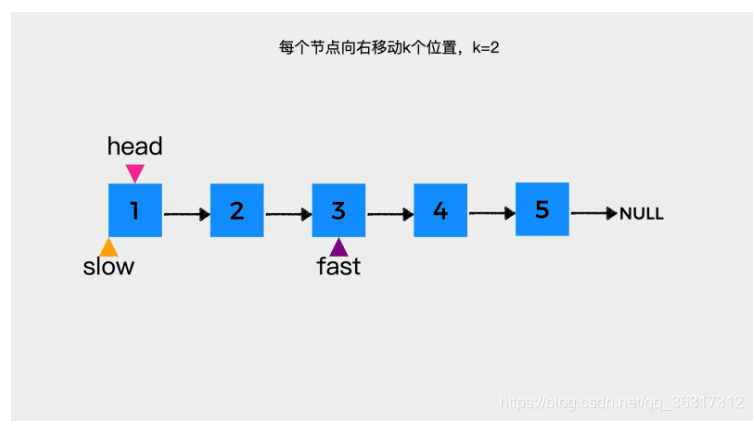
3、慢指针slow和快指针fast同时向前移动,每次移动一步,直到快指针fast指向链表的尾节点.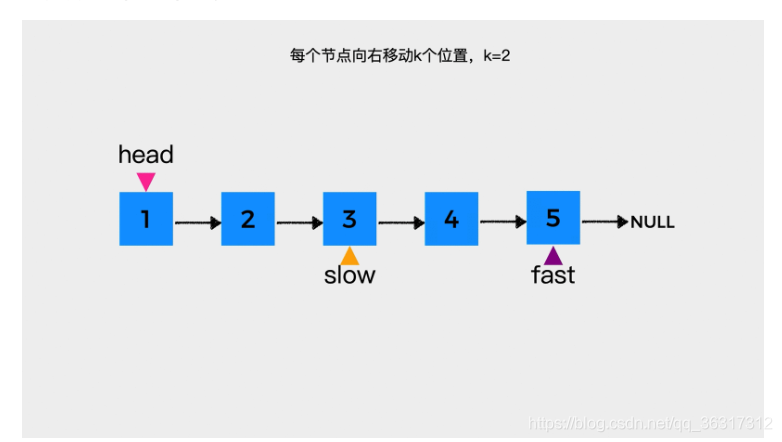
4、慢指针slow所指节点的下一个节点就是倒数第K个节点,要做的就是将快指针fast所指的尾节点的后继指针指向链表头节点,使链表成环。然后,倒数第K个节点作为链表旋转后的新的头节点,指针slow所指节点作为新的尾节点。
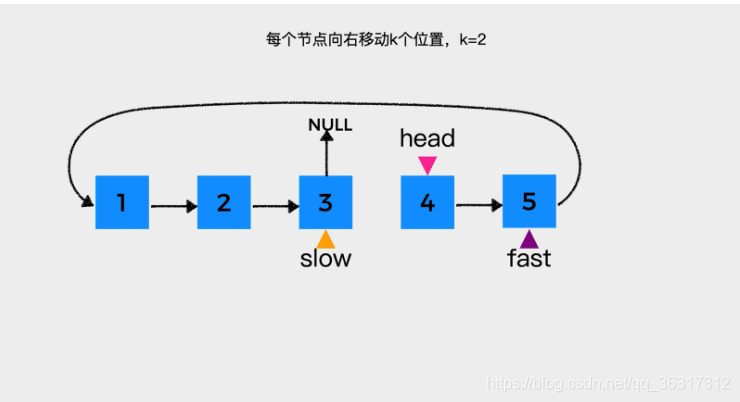
java代码
class Solution {
public ListNode rotateRight(ListNode head, int k) {
if(head == null ){
return head;
}
// 总节点个数
int sum_len = calculateLen(head);
k = k% sum_len;
//快慢指针初始化,指向头节点
ListNode slow = head;
ListNode fast = head;
//快指针向前移动k步
for(int i=0;i<k;i++){
fast = fast.next;
}
while(fast.next != null) {
fast = fast.next;
slow = slow.next;
}
//快指针在链表末尾,然后进行连接,后继节点指向头节点,成环
fast.next = head;
//新头节点是慢指针所指的下一个节点
head = slow.next;
//慢指针所指 的节点的下一个节点为null
slow.next = null;
return head;
}
private int calculateLen(ListNode head){
int len = 0;
while (head!=null) {
head = head.next;
len++;
}
return len;
}
}
141、环形链表
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
如果链表中存在环,则返回 true 。 否则,返回 false 。
示例1:
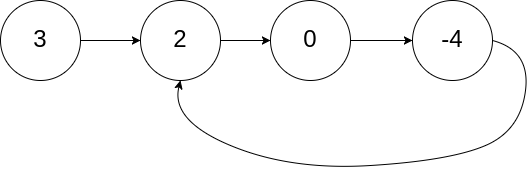
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
解题思路:使用快慢指针,主要是判断是否成环,当块指针与慢指针相遇重合时,则代表有环。
具体步骤:首先初始化快慢指针,快指针速度是慢指针的两倍,如果快慢指针重合时,返回true
python代码
class Solution:
def hasCycle(self, head: ListNode) -> bool:
fast = slow = head
#判断fast 和fast.next不为空
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast ==slow:
return True
return False
java代码
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast!=null && fast.next!=null) {
fast = fast.next.next;
slow = slow.next;
if(fast == slow){
return true;
}
}
return false;
}
}
142、环形链表II
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
示例: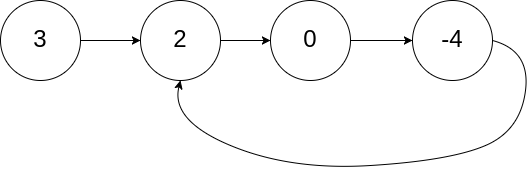
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
**解题思路:**链表中存在环,则 \textit{fast}fast 指针最终将再次与 \textit{slow}slow 指针在环中相遇。再计算一下相遇点与入环点的关系
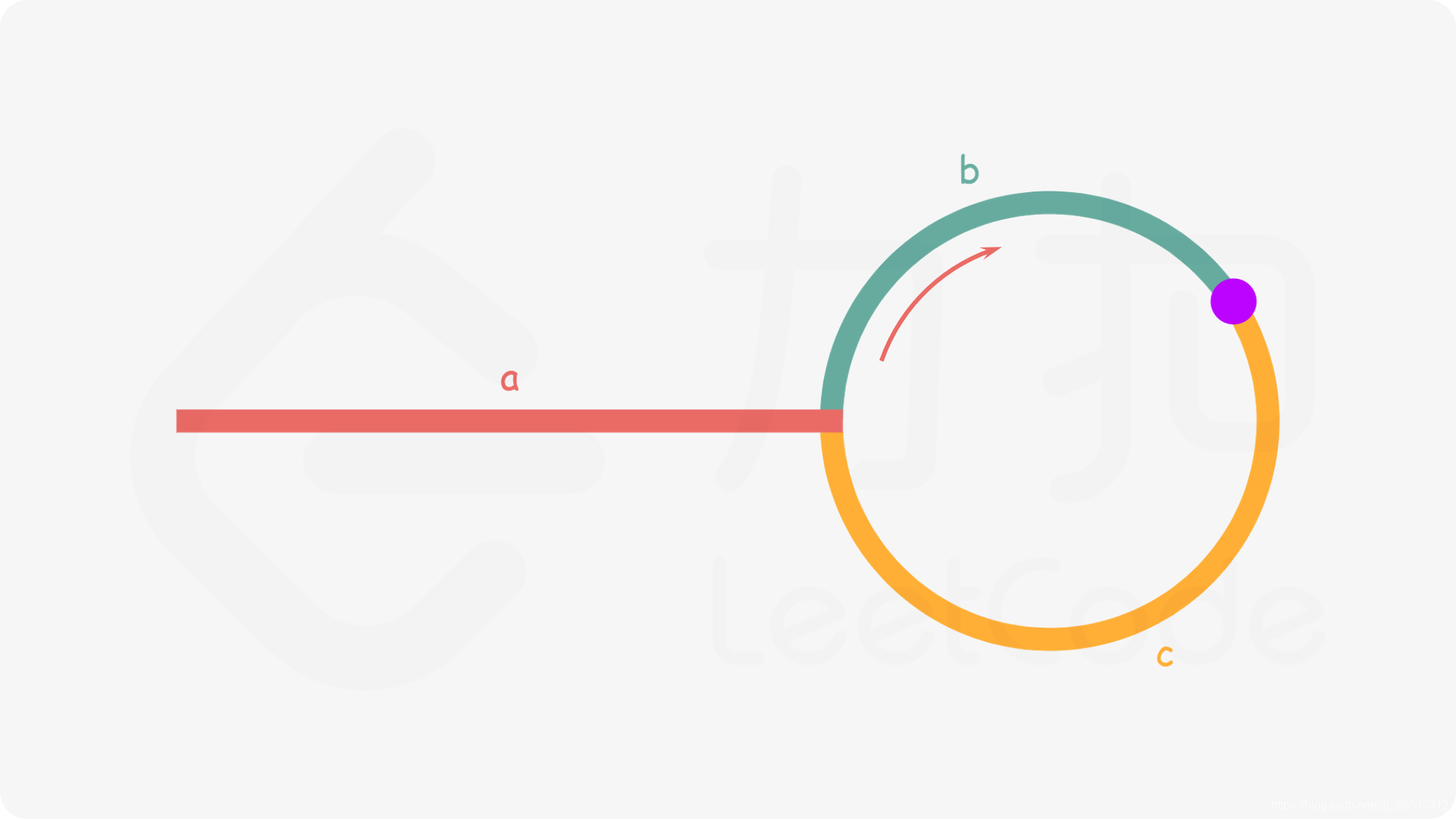
如下图所示,设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b 的距离与 fast 相遇。此时,fast 指针已经走完了环的 n 圈,因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc。根据题意,任意时刻,fast 指针走过的距离都为 slow 指针的 2 倍。
因此,我们有 a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c) 。
我们会发现:从相遇点到入环点的距离加上 n-1 圈的环长,恰好等于从链表头部到入环点的距离。
因此,当发现 slow 与fast 相遇时,我们再额外使用一个指针 ptr起始,它指向链表头部;随后,它和slow 每次向后移动一个位置。最终,它们会在入环点相遇。
java 代码
public class Solution {
public ListNode detectCycle(ListNode head){
ListNode fast,slow;
fast=slow=head;
while(fast !=null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if(fast==slow){
slow = head;
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
return null;
}
}
掌握了上面的双指针的左右指针和快慢指针的具体方法,相信看过的小伙伴们也能够举一反三了。
同时相信有了刷题的技巧,再加上一本总结资料也能够更加深刻与系统。labuladong 的算法小抄和halfrost的LeetCode刷题手册,对我受益匪浅,现在推荐给大家,大家一起刷题,共勉!


同时需要这些资料的小伙伴们,可以关注一下“研行笔录”微信公众号,回复leetcode即可,还不快来领取leetcode刷题大礼包。























 316
316












