数据结构与算法-07平衡二叉树-03

原创 于 2025-01-14 21:01:24 发布 · 381 阅读 · 6 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #开发语言 #数据结构 #java

AVL树删除节点

空树

如果树为空删除失败

  if (root == null) return null;

记录删除结果

定义节点对象记录临时记录删除结果。

AVLNode resultNode = null;

查找删除的节点值

当前节点数据和要删除的数据一致

if(root.left == null && root.right==null){ //叶节点
    
}
else if(root.right == null){  //右子树为空

}else if(root.left == null){ //左子树为空

}else{ //左右子树都不为空

}
如果删除节点是叶节点

检查resultNode是否改变，如果没有改变说明待删除的节点是叶节点，直接返回null，将当前节点连接断开。

if(root.left == null && root.right==null){ //叶节点
    
}
右子树为空

右子树为空需要记录左子树节点 。

else if (root.right == null) {
    resultNode = root.left;
}
左子树为空
else if (root.left == null) {
    resultNode = root.right;
}
左右子树都不为空

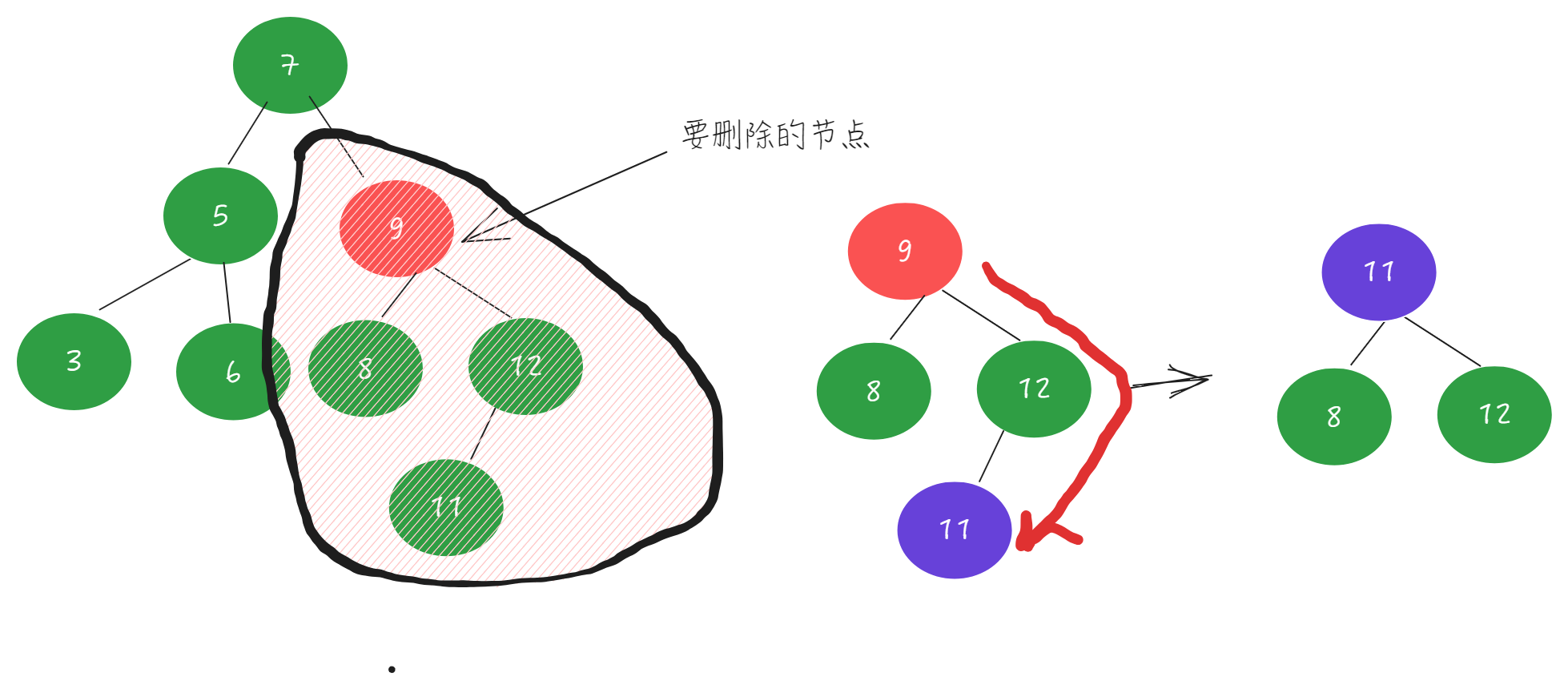
image-20240914145247479

获取当前节点的右子树最小节点
private AVLNode minNode(AVLNode curr) {
    AVLNode tmp = curr;
    while (tmp.left != null) {
        tmp = tmp.left;
    }
    return tmp;
}
  • 获取当前节点的右侧最小节点
 AVLNode minNode = minNode(node.right);
  • 更新最小节点的右侧节点
minNode.right = remove(node.right, minNode.val);
  • 更新最小节点的左侧节点
minNode.left = node.left;
  • 记录最小节点

最小节点更新替换了删除的节点(curr), 将其记录到resultNode

resultNode = minNode;

当前节点数据数据值大于要删除的值

查找左子树进行删除操作，递归找左子树。

node.left = remove(node.left, val);
resultNode = node;

当前节点的数据值小于要删除的值

递归右子树找到节点删除。

node.right = remove(node.right, val);
resultNode = node;

对ResultNode进行调整

更新高度

 resultNode.height = getHeight(resultNode);

获取平衡因子

删除之后可能要树不平衡，因此要检查平衡因子。

int bf = balanceFactor(resultNode);

调整为平衡树

if (bf > 1 && balanceFactor(resultNode.left) >= 0) {
    resultNode = rightRotate(resultNode);
} else if (bf < -1 && balanceFactor(resultNode.right) <= 0) {
    resultNode = leftRotate(resultNode);
} else if (bf > 1 && balanceFactor(resultNode.left) < 0) {
    resultNode.left = leftRotate(resultNode.left);
    resultNode = rightRotate(resultNode);
} else if (bf < -1 && balanceFactor(resultNode.right) > 0) {
    resultNode.right = rightRotate(resultNode.right);
    resultNode = leftRotate(resultNode);
}

return resultNode;

AVLTree

package com.ffyc.avl;

import com.ffyc.avl.util.TreePrint;

public class AVLTree {

    /**
     * 正数， 负数  , 0
     *
     * @param curr
     * @return
     */
    private int balanceFactor(AVLNode curr) {
        return getHeight(curr.left) - getHeight(curr.right);
    }

    private int getHeight(AVLNode curr) {
        if (curr == null) return 0;
        return 1 + Math.max(getHeight(curr.left), getHeight(curr.right));
    }

    private AVLNode rightRotate(AVLNode curr) {
        AVLNode X = curr.left;
        AVLNode U = X.right;

        X.right = curr;
        curr.left = U;

        X.height = getHeight(X);
        curr.height = getHeight(curr);
        return X;
    }


    private AVLNode leftRotate(AVLNode curr) {
        AVLNode X = curr.right;
        AVLNode U = X.left;
        X.left = curr;
        curr.right = U;
        X.height = getHeight(X);
        curr.height = getHeight(curr);
        return X;
    }

    public AVLNode insert(AVLNode root, int val) {
        if (root == null) {
            root = new AVLNode(val);
            return root;
        }
        if (val < root.val) {
            root.left = insert(root.left, val);
        } else {
            root.right = insert(root.right, val);
        }
        root.height = getHeight(root);
        int bf = balanceFactor(root);

        //bf>1 左    balanceFactor(root.left) > 0 左
        if (bf > 1 && balanceFactor(root.left) > 0) {
            return rightRotate(root);
        }

        //RR
        if (bf < -1 && balanceFactor(root.right) < 0) {
            return leftRotate(root);
        }

        //LR
        if (bf > 1 && balanceFactor(root.left) < 0) {
            root.left = leftRotate(root.left);
            return rightRotate(root);
        }
        //RL
        if (bf < -1 && balanceFactor(root.right) > 0) {
            root.right = rightRotate(root.right);
            return leftRotate(root);
        }
        return root;
    }

    private AVLNode minNode(AVLNode curr) {
        AVLNode tmp = curr;
        while (tmp.left != null) tmp = tmp.left;
        return tmp;
    }

    public AVLNode remove(AVLNode root, int val) {
        if (root == null) return null;
        AVLNode resultNode;
        if (val == root.val) {
            if (root.left == null && root.right == null) {//叶节点
                return null;
            } else if (root.left == null) {
                resultNode = root.right;
            } else if (root.right == null) {
                resultNode = root.left;
            } else {//左右都不为空
                AVLNode min = minNode(root.right);
                min.right = remove(root.right, min.val);
                min.left = root.left;
                resultNode = min;
            }
        } else if (val < root.val) {
            root.left = remove(root.left, val);
            resultNode = root;
        } else {
            root.right = remove(root.right, val);
            resultNode = root;
        }

        resultNode.height = getHeight(resultNode);
        int bf = balanceFactor(resultNode);

        if (bf > 1 && balanceFactor(root.left) >= 0) {//LL
            return rightRotate(resultNode);
        }
        if (bf < -1 && balanceFactor(resultNode.right) <= 0) {
            return leftRotate(resultNode);
        }
        if (bf > 1 && balanceFactor(resultNode.left) < 0) {
            resultNode.left = leftRotate(resultNode.left);
            return rightRotate(resultNode);
        }
        if (bf < -1 && balanceFactor(resultNode.right) > 0) {
            resultNode.right = rightRotate(resultNode.right);
            return leftRotate(resultNode);
        }
        return resultNode;

    }

    public static void main(String[] args) {
        AVLTree tree = new AVLTree();
        AVLNode root = tree.insert(null, 35);
        root = tree.insert(root, 25);
        root = tree.insert(root, 50);
        root = tree.insert(root, 40);
        root = tree.insert(root, 55);
        root = tree.insert(root, 38);
        root = tree.insert(root, 15);
        root = tree.insert(root, 12);
        TreePrint<Integer> print = new TreePrint<>();
        print.print(root);
        root = tree.remove(root, 25);
//      root = tree.remove(root, 50);
        print.print(root);
//      root = tree.remove(root, 35);
//      print.print(root);

    }

}

辅助方法：打印二叉树

/**
 * 中序图形效果打印
 *
 * @param <E>
 */
public class TreePrint<E> {
    private final List<AvlNode> mid = new ArrayList<>();//记录bst树的节点
    private final Map<AvlNode, Integer> map = new HashMap<>();//记录节点及位置

    private Queue<E> queue = new ArrayDeque<>();
    private AvlNode root;

    public TreePrint() {
    }

    public TreePrint(AvlNode root) {
        this.root = root;
    }

    /**
     * 中序遍历
     *
     * @param root 树的根节点
     */
    public void inOrder(AvlNode root) {
        if (root == null) {
            return;
        }
        inOrder(root.left);
        mid.add(root);
        inOrder(root.right);
    }

    /**
     * 使用Map记录节点及位置
     *
     * @param root
     */
    public void init(AvlNode root) {
        if (root == null) {
            return;
        }
        inOrder(root);
        for (int i = 0; i < mid.size(); i++) {
            map.put(mid.get(i), i);
        }
    }

    /**
     * 打印同一层的节点,使用|线和值进行拼接打印
     *
     * @param TreeNodes
     */
    void printLevelTreeNodes(List<AvlNode> TreeNodes) {
        StringBuilder VLine = new StringBuilder();
        StringBuilder dataLine = new StringBuilder();
        StringBuilder line = new StringBuilder();
        int lastTreeNodeIndex = 0;
        int lastRightIndex = 0;

        for (AvlNode TreeNode : TreeNodes) {
            int x = map.get(TreeNode);
            String addEmpty = getEmpty(x - lastTreeNodeIndex);
            lastTreeNodeIndex = x;
            VLine.append(addEmpty).append("|");//竖线拼接
            dataLine.append(addEmpty).append(TreeNode.val); //值拼接

            AvlNode left = TreeNode.left;
            AvlNode right = TreeNode.right;
            String leftLine = null;
            String rightLine = null;

            int leftIndex = -1;
            int rightIndex = -1;
            if (left != null) {
                leftIndex = map.get(left);
                leftLine = getLineToChildren(x - leftIndex);
            }
            if (right != null) {
                rightIndex = map.get(right);
                rightLine = getLineToChildren(rightIndex - x);
            }

            String curLine = (leftLine == null ? "" : leftLine) + "|" + (rightLine == null ? "" : rightLine);
            if (leftLine == null && rightLine == null) curLine = "";
            //线段之间的间隔
            int dif = (leftIndex == -1 ? x : leftIndex) - lastRightIndex;
            String difEmpty = getEmpty(dif);
            line.append(difEmpty).append(curLine);//拼接线段
            lastRightIndex = rightIndex == -1 ? x : rightIndex;
        }
        System.out.println(VLine + "\n" + dataLine + "\n" + line);
    }

    String getEmpty(int x) {
        StringBuilder empty = new StringBuilder();
        for (int i = 0; i < x; i++) {
            empty.append("\t");
        }
        return empty.toString();
    }


    //链接子线段的长度
    String getLineToChildren(int end) {
        StringBuilder line = new StringBuilder();
        if (end == 0) return line.toString();
        for (int i = 0; i < end; i++) {
            line.append("____");
        }
        return line.toString();
    }

    /**
     * 扫描每一行中每一个节点的左右节点
     *
     * @param lineTreeNodes 每一行的节点
     */
    public void topToDownLevelPrint(List<AvlNode> lineTreeNodes) {
        if (lineTreeNodes.isEmpty()) return;

        printLevelTreeNodes(lineTreeNodes);//打印同一层的节点

        List<AvlNode> children = new ArrayList<>();  //记录当前节点下的所有子节点
        //记录当前节点下的所有左右节点
        for (AvlNode currentTreeNode : lineTreeNodes) {
            if (currentTreeNode.left != null) children.add(currentTreeNode.left);
            if (currentTreeNode.right != null) children.add(currentTreeNode.right);
        }
        topToDownLevelPrint(children);//递归打印下一层节点
    }

    public void print(AvlNode root) {
        init(root);
        topToDownLevelPrint(new ArrayList<AvlNode>() {{
            add(root);
        }});
    }
}
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值