数据结构与算法-04二叉树-03

构建二叉搜索树

添加节点

public TreeNode insert(TreeNode root, int val) {
    TreeNode newNode = new TreeNode(val);
    if (root == null) {
        root = newNode;
        return root;
    }

    if (val < root.val) {
        root.left = insert(root.left, val);
    } else {
        root.right = insert(root.right, val);
    }
    return root;
}

删除节点

递归方式查找节点是否是要删除的节点

跳出条件: 如果是叶节点，即left，right为null 删终止

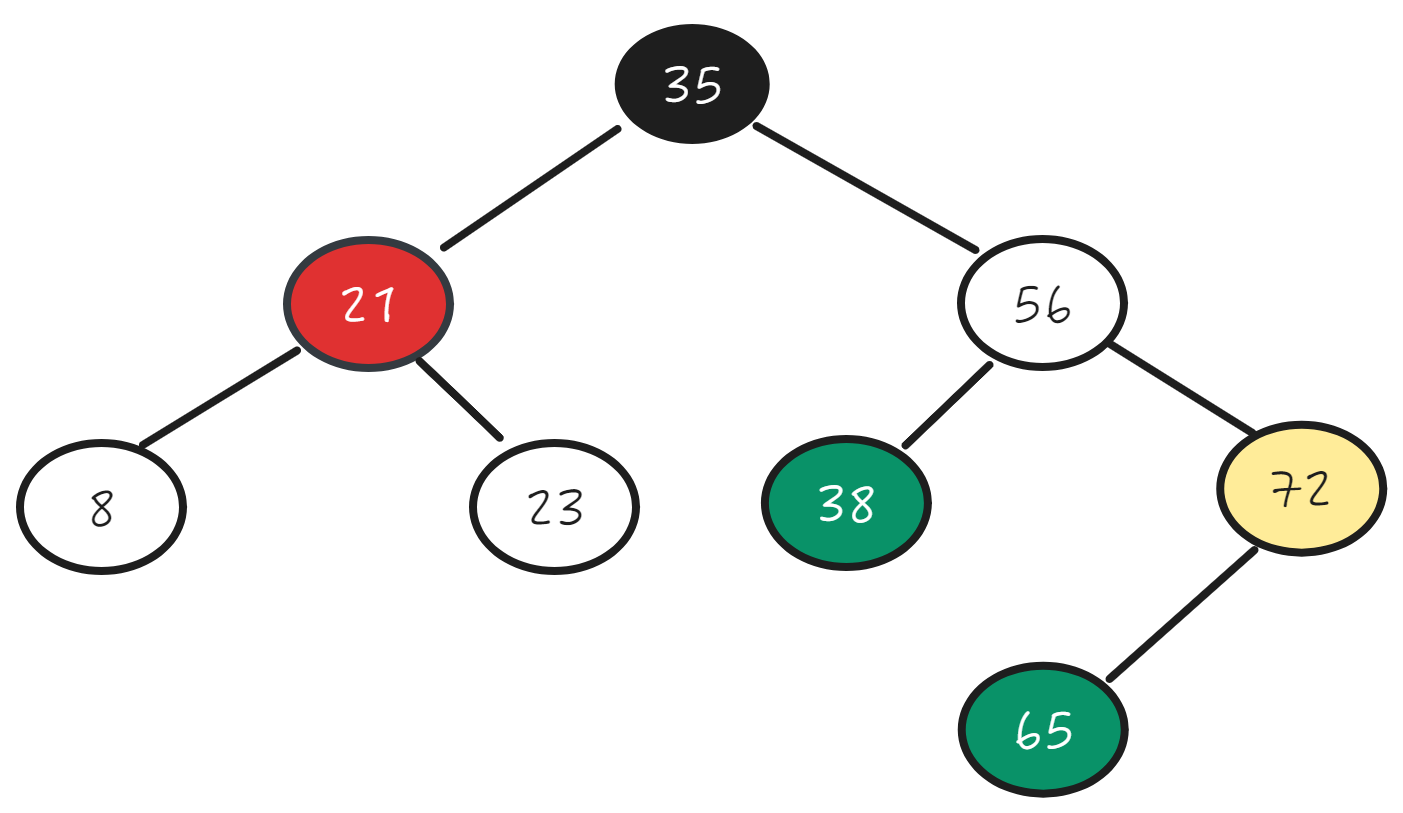
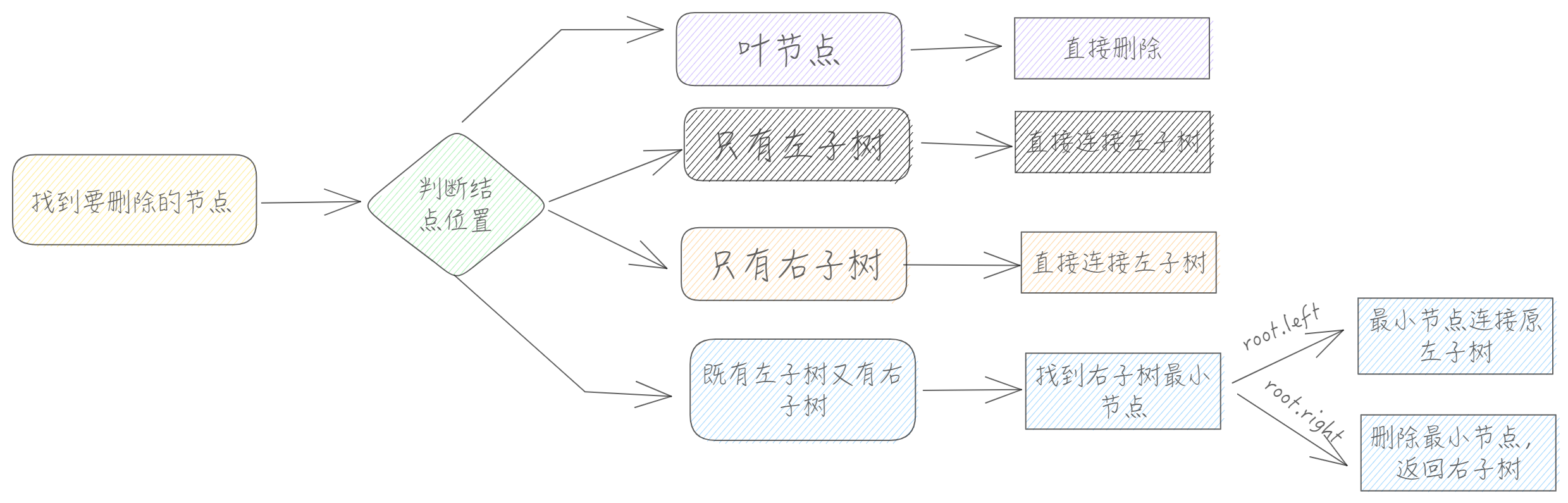
Hibbard Deletion:One efficient way to do this, as discovered by Thomas Hibbard in 1962, is to swap the node to be deleted with its successor. The successor to a key is the next largest key in the tree and is conveniently found as the minimum key in the right subtree of the node to be deleted.

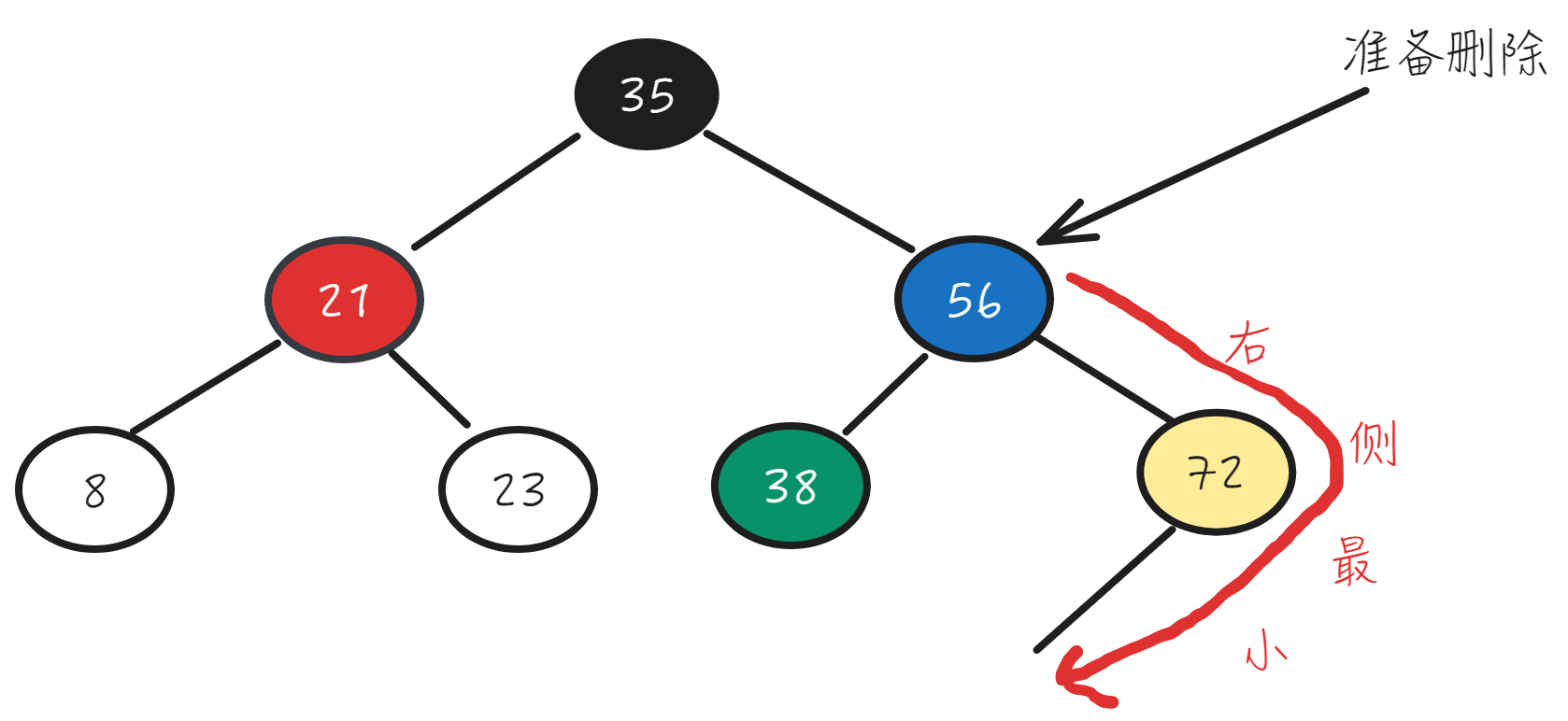
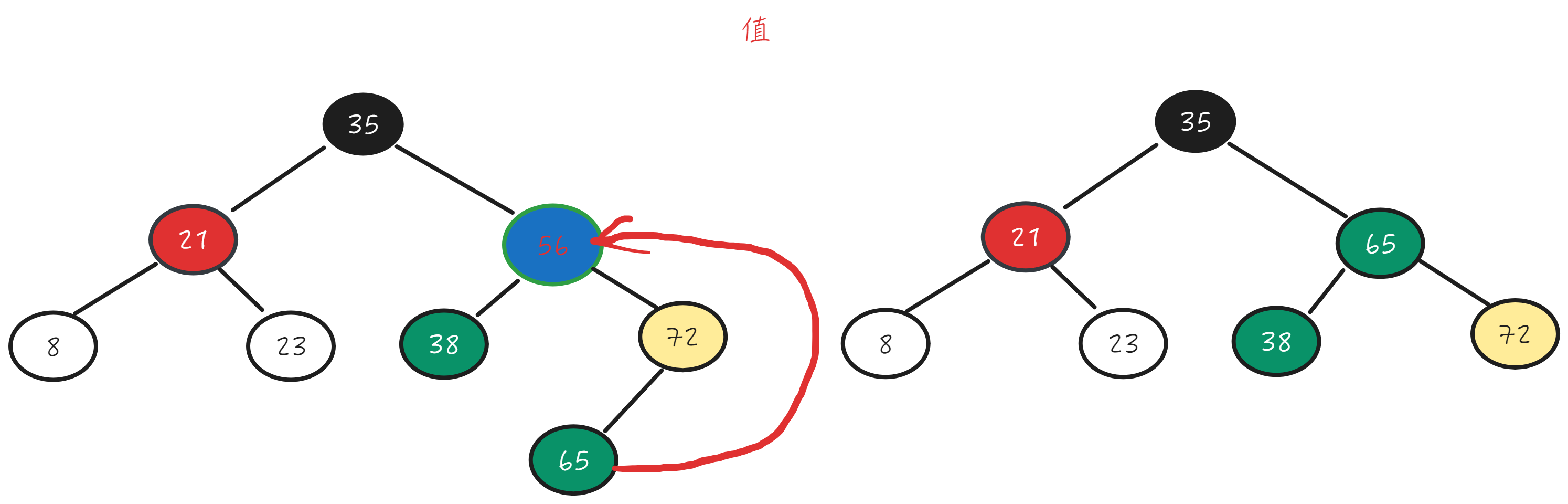
 public TreeNode remove(TreeNode root, int val) {

        if (root.val == val) { //找到节点
            //要删除的节点是叶节点
            if (root.left == null && root.right == null) {
                return null;
            }
            //要删除的节点只有右节点
            if (root.left == null) {
                return root.right;
            }
            //要删除的节点只有左节点
            if (root.right == null) {
                return root.left;
            }
            //要删除的节点左右都不为空
            //找到当前节点的子树中的最小节点
            TreeNode minNode = minNode(root.right);
            minNode.right = remove(root.right, minNode.val);
            minNode.left = root.left;
            return minNode;
        } else if (val < root.val) {
            root.left = remove(root.left, val);
        } else {
            root.right = remove(root.right, val);
        }
        return root;
    }

查询

public void print(TreeNode root){
    if(root == null) return;
    print(root.left);
    System.out.print(root.val+"\t");
    print(root.right);
}

测试

public static void main(String[] args) {
        BstTree tree = new BstTree();
        TreeNode root = tree.insert(null, 15);
        root = tree.insert(root, 8);
        root = tree.insert(root, 25);
        root = tree.insert(root, 5);
        root = tree.insert(root, 12);
        root = tree.insert(root, 20);
        root = tree.insert(root, 55);

        tree.print(root);
        System.out.println();
        tree.remove(root, 15);
        tree.print(root);

    }