第12章——投影与三位视觉

投影

仿射变换和透视变换

POSIT：3D姿态估计

立体成像

两台摄像机的立体成像过程包括：

1. 消除畸变
2. 摄像机矫正
3. 图像匹配
4. 重投影

三角测量

十分理想化的模型
摄像机前向平行排列：两摄像机①像平面共面；②光轴平行；③距离一定；④焦距相同；⑤校准后主点具有相同的像素坐标⑥图像平面行对准

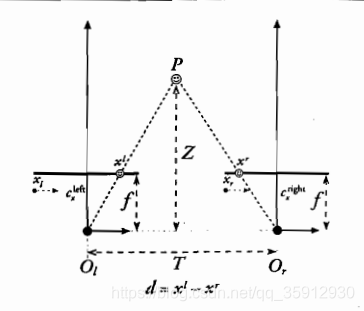
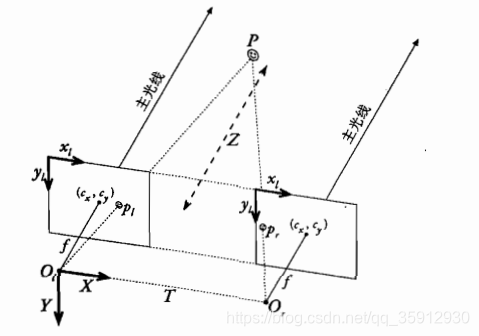
-c_l，c_r：左右像平面的主点。
-p_l，p_r：点P在左右图像（投影）平面的成像点。
-x_l，x_r：p_l，p_r相应的横坐标
-T：
-Z：

视差：d = x_l - x_r
由三角形相似可知：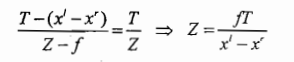
由表达式可以看出：

1. 深度和视差成反比；
2. 深度和视差的关系为非线性的；
3. 当视差较大时，微小的视差几乎不影响深度的变化；当视差趋于0时，微小的视差会引起巨大的深度变化。
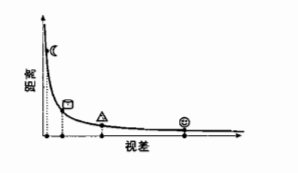   视差较小时才能较为精确判断深度。

而现实问题上，两相机很难做到前向平行排列，比如图像平面不共面（如下图）

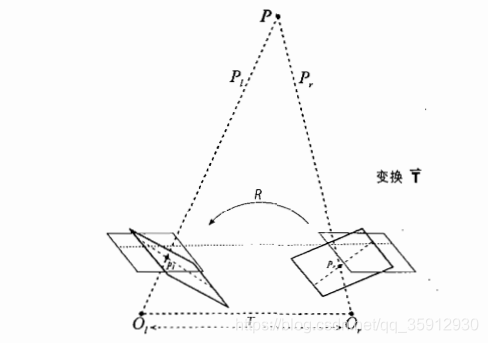
如果物理上矫正难免存在一些误差，因此我们需要用数学方法去补偿（矫正）。但是呢，为了使数学变换更简单（稍稍矫正），往往还要加上必要的物理对准，比如使摄像机尽可能前向对准、水平对准。

摄像机同步？？？

同针孔摄像机模型，先讨论最简单的情况，然后通过转换，把复杂问题简单化
牢记目的：摄像机前向平行排列，为此引入对极几何
☟☟☟☟☟☟

基础知识

对极几何

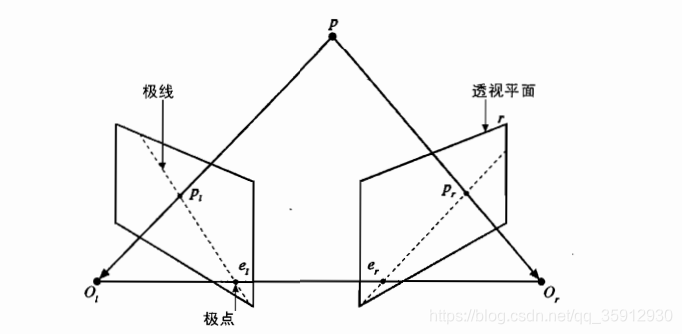
-O_l， O_r：连摄像机的孔。
极点：O_l， O_r的连线与图像（投影）平面的交点。
极线：投影点p_l， p_r分别于与极点e_l， e_r的连线。
极面：观测点P与两个孔，三点确定的面PO_lO_r。

** 本征矩阵和基础矩阵**

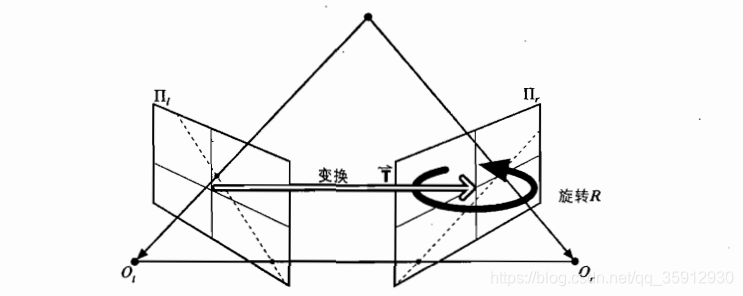
本征矩阵E：1. 内容：
2. 作用：
基础矩阵F：
4. 内容：
5. 作用：将一台摄像机的图像（投影）平面上的点的像素坐标与另一台摄像机的图像平面上的点关联起来。

极线的计算

立体标定

目的：两摄像机的图像平面精确的落在同一平面上，即共面。
首先对单目摄像头进行标定易得相应的畸变参数与内参矩阵。
假设空间中有一点P，由畸变参数与内参矩阵可由图像（投影）平面的像素点得得到其在左右摄像机坐标系下的点分别为P_l，P_r。由PnP可得相应的外参矩阵。
P_r = P·R_r +T_r ①
P_l = P·R_l +T_l ②
假设R，T分别为从左摄像机的坐标系到 右摄像机的旋转矩阵和平移向量，则有
P_r = P_l·R + T ③
综合①②③得：
R = R_r · R_l^T
T = T_r - R·T_l

注意：

1. 双目摄像机标定和单目摄像机标定最主要的区别就是双目摄像机需要标定出左右摄像机坐标系之间的相对关系
2. 双目摄像机分析中往往以左摄像机为主坐标系
3. 经过立体标定后，两摄像机坐标系相同，但是好像不是正向的，是否物理对准后近似认为正向，标定只是用数学方法让两坐标系严格相同，图像平面共面。

立体校正

目的：求旋转矩阵与平移向量，使两摄像机的图像平面精确地行对准。

左右图像平面共面且行对准 <=> 极点无穷远 <=>
作用：同时像素的每一行都是极线，

• 方便视差的计算；
• 由于匹配点一定落在同一像素行上，减少匹配区域，加快运算效率。

校正算法：

1. 非标定立体矫正：[Hartley算法]
2. 标定立体矫正：[Bouguet算法]
   校正映射

立体匹配

只有在两个摄像机的重叠视图内的可视区域才能被计算，很显然，如果不在重叠视图内，其中一个摄像机将不起作用，不能实现双目。
这样就解释了，我们把摄像机尽量前向平行，是为了获得更大的重叠试图。
立体匹配算法：BM算法

维重投影获得深度映射

来自运动的结构

二维和三维下的直线拟合