机器学习笔记（七）：概率图模型

最新推荐文章于 2024-10-28 17:18:30 发布
原创 最新推荐文章于 2024-10-28 17:18:30 发布 · 809 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#机器学习 #概率图 #马尔可夫随机场 #条件随机场

本文介绍了概率图模型中的三种重要模型：隐马尔科夫模型（HMM）、马尔科夫随机场（MRF）和条件随机场（CRF）。HMM是最简单的动态贝叶斯网，MRF是满足马尔可夫性的无向图模型，而CRF则是一种判别式的无向图模型，广泛应用于序列标注任务。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

机器学习最重要的任务，是根据一些已观察到的证据（例如训练样本）来对感兴趣的未知变量（例如类别标记）进行估计和推测。概率模型提供了一种描述框架，将学习任务归结为计算变量的概率分布。概率图模型（probabilistic graphical model,简称PGM）是一类用图来表达变量相关关系的概率模型，它以图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”。

根据边的性质不同，概率图模型可大致分为两类：第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网；第二类是使用无向图表示变量间的相关关系，称为无向图模型或马尔科夫网（Markov network）.

关于贝叶斯网在上一篇文章中已有介绍，本文主要介绍马尔科夫网。

目录

  • 隐马尔科夫模型
  • 马尔科夫随机场
  • 条件随机场

 

 

一、隐马尔科夫模型(Hidden Markov Model,简称HMM)

隐马尔科夫模型是结构最简单的动态贝叶斯网，其基本思想来源于马尔可夫过程，可看作是一个含有隐含未知参数的马尔可夫过程。（对马尔可夫过程不了解的同学可参考百度百科中的介绍

https://baike.baidu.com/item/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E8%BF%87%E7%A8%8B/2952385）

一个对马尔科夫模型直观的描述如下图所示

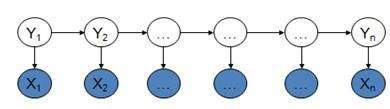
上图中的变量可分为两组，一组是状态变量{y1,y2,…,yn}，yi∈У表示系统在第i时刻的状态，通常假定状态变量是隐藏的、不可被观测的，因此状态变量亦称隐变量。第二组是观测变量即可以被观测到的变量{x1,x2,…,xn}，其中xi∈Х表示第i时刻的观测值。观测变量的取值仅依赖于状态变量，即xt由yt确定；而yt仅依赖于上一个时刻的状

最低0.47元/天 解锁文章

200万优质内容无限畅学
机器学习--概率图模型
luckmia的博客
07-18 975
一、隐马尔可夫模型 隐马尔可夫模型是结构最简单的动态贝叶斯网，这是一种著名的有向图模型，主要用于时序数据建模，在语音识别、自然语言处理等领域有广泛应用。 　 首先我们来看看什么样的问题解决可以用HMM模型。使用HMM模型时我们的问题一般有这两个特征：１）我们的问题是基于序列的，比如时间序列，或者状态序列。２）我们的问题中有两类数据，一类序列数据是可以观测到的，即观测序列；而另一类数据是...
机器学习笔记 第十四章概率图模型
qq_53034510的博客
08-19 963
如图14.3所示，如果从结点集A中的结点到B中的结点都必须经过结点集C中的结点，则称结点集A和B被结点集C分离，C称为“分离集”。概率图模型是一类用图来表达变量关系的概率模型，最常见的是用一个结点表示一个或一组随机变量，边表示变量间的概率相关关系，即“变量关系图”。均依赖于其他变量z，图(b)中。一个结点只有在接收到来自其他所有结点的消息后才能向另一个结点发消息，且结点的边际分布正比于它所接收的消息的乘积，即。局部马尔可夫性：给定某变量的邻接变量，则该变量条件独立于其他变量，形式化地说，令V为图的结点集，
PGMIntro概率图模型
weixin_43458628的博客
04-14 467
概率图模型 概率图模型使用图的方式表示概率分布。为了在图中添加各种概率，首先总结一下随机变量分布的一些规则： KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ &Sum\ Rule:p(x… 可以看到，在链式法则中，如果数据维度特别高，那么的采样和计算非常困难，我们需要在一定程度上作出简化，在朴素贝叶斯中，作出了条件独立性假设。在 Markov 假设中，给定数据的维度是以时间顺序出现的
机器学习 | 概率图模型
"You are worthy! You can do it!"
12-22 1200
见微知著，睹始知终。见到细微的苗头就能预知事物的发展方向，能透过微小的现象看到事物的本质，推断结论或者结果。概率模型为机器学习打开了一扇新的大门，将学习的任务转变为计算变量的概率分布。实际情况中，各个变量间存在显式或隐式的相互依赖，如朴素贝叶斯方法直接基于训练数据去求解变量的联合概率分布在时间复杂度还是空间复杂度均是不可行、不划算的。直接基于训练数据求解变量联合概率分布困难。Probabilistic Graphical Model，简称PGM，就是用图来表示变量概率间的依赖关系。
机器学习总结——概率图模型
guolinsen123的专栏
10-31 841
文章目录简介常见图模型NLP中概率图模型演变隐马尔可夫模型马尔科夫链参数三个基本问题存在的问题随机场马尔可夫随机场势函数团&最大团基于最大团定义的联合概率分离集性质最大熵马尔科夫随机场HMM与MEMM的区别优点缺点标记偏置问题条件随机场参数化形式三个基本问题优点与马尔科夫随机场区别与MEMM区别近似推断采样MCMCMetropolis-Hastings吉布斯采样变分推断 概率图模型是一类用...
机器学习笔记之概率图模型(七)精确推断之变量消去法
静静的学习就好
10-24 1929
上一节介绍了推断的本质以及推断的具体方法。本节将介绍精确推断方法中的变量消去法(Variable Elimination,VE)
机器学习笔记之概率图模型(六)推断基本介绍
静静的学习就好
10-22 1435
前面部分分别介绍了贝叶斯网络(Bayessian Network)和马尔可夫随机场(Markov Random Field)的结构表示(Representation)，本节开始将介绍概率图模型的第二部分——推断(Inference)。
机器学习笔记之概率图模型(八)信念传播(Belief Propagation,BP)(基于树结构)
静静的学习就好
10-25 3052
上一节介绍了精确推断中的变量消去法，本节将针对变量消去法的弊端，介绍信念传播。
机器学习基础（七）：概率图模型（HMM、MRF、CRF、话题模型、推断方法）
zero_ling
09-28 1805
7、概率图模型 概率模型probabilistic model：提供一种描述框架，将学习任务归结于计算变量的概率分布，核心是如何基于可观测变量推测出未知变量的条件分布 → ①生成式generative模型：考虑联合分布P(Y,R,O) ②判别式discriminative模型：考虑条件分布P(Y,R|O) 由①或②得到条件概率分布P(Y|O) （Y：所关心的变量集合；O：可观测变量集合；R：其他变量的集合） 概率图模型probabilistic graphical model：一类用图来表达变量相关关系的概
机器学习7-概率图模型-2020.pdf
12-20
机器学习7-概率图模型-2020.pdf
概率图模型
07-03
Statistical learning refers to a set of tools for modeling and understanding complex datasets. It is a recently developed area in statistics and blends with parallel developments in computer science and, in particular, machine learning. The field encompasses many methods such as the lasso and sparse regression, classification and regression trees, and boosting and support vector machines. With the explosion of “Big Data” problems, statistical learning has be- come a very hot field in many scientific areas as well as marketing, finance, and other business disciplines. People with statistical learning skills are in high demand. One of the first books in this area—The Elements of Statistical Learning (ESL) (Hastie, Tibshirani, and Friedman)—was published in 2001, with a second edition in 2009. ESL has become a popular text not only in statis- tics but also in related fields. One of the reasons for ESL’s popularity is its relatively accessible style. But ESL is intended for individuals with ad- vanced training in the mathematical sciences. An Introduction to Statistical Learning (ISL) arose from the perceived need for a broader and less tech- nical treatment of these topics. In this new book, we cover many of the same topics as ESL, but we concentrate more on the applications of the methods and less on the mathematical details. We have created labs illus- trating how to implement each of the statistical learning methods using the popular statistical software package R . These labs provide the reader with valuable hands-on experience.
机器学习之概率图模型
lankuohsing的博客
08-26 638
文章目录0. 背景介绍1. 隐马尔科夫模型（Hidden Markov Model, HMM）1.1. HMM的数学定义1.2. HMM的实际应用问题描述1.3. 马尔科夫随机场（Markov Random Field, MRF）2. 条件随机场（Conditional Random Field， CRF）2.1. CRF的数学定义2.2. 特征函数的例子 参考资料： 《机器学习》——周志华 https://blog.youkuaiyun.com/continueoo/article/details/7789358.
概率图模型基础
weixin_34320159的博客
02-28 210
一、概念引入 　　很多事情是具有不确定性的。人们往往希望从不确定的东西里尽可能多的得到确定的知识、信息。为了达到这一目的，人们创建了概率理论来描述事物的不确定性。在这一基础上，人们希望能够通过已经知道的知识来推测出未知的事情，无论是现在、过去、还是将来。在这一过程中，模型往往是必须的，什么样的模型才是相对正确的？这又是我们需要解决的问题。这些问题出现在很多领域，包括模式识别、差错控制编码等。 ...
机器学习系列：概率图模型
qq_39068872的博客
03-28 349
文章目录1. Introduction2. 有向图-贝叶斯网络3.无向图-马尔科夫网络（马尔科夫随机场）4 两种图的转换-道德图5 因子图 1. Introduction 概率图模型使用图的方式表示概率分布。为了在图中添加各种概率，首先总结一下随机变量分布的一些规则： Sum Rule:p(x1)=∫p(x1,x2)dx2Product Rule:p(x1,x2)=p(x1∣x...
机器学习基础 之 概率图模型
04-16 666
概率图模型就是基于概率构建的图结构模型，使用该模型来进行数据的分类，有多种类型的方法来进行模型的求解，包括马尔科夫模型，随机场等..
人工智能（5）——————机器学习之概率图模型
最新发布
2301_79704829的博客
10-28 1170
概率图模型，作用就是来给人们带来对模型最直观的体验的，而有向图和无向图之分，只是为了概率图模型能更好的适配不同数据集，不同特征相关性下的所有模型，万变不离其宗，所有网络模型的最终结果，都是通过先验概率与后验概率相结合，对模型参数进行处理。当然，不同的模型有着各自的优缺点，需要结合具体实际来选取不同的模型网络。
机器学习 (第9章 概率图模型)
komjay的博客
12-25 3013
对于一个很大的贝叶斯网络，我们需要有一个很高效的方法的快速辨别两个变量之间是不是独立的，但我们这里考虑条件独立性，条件独立性不同于独立性，条件独立性，必须要在某一条件下，考虑另外两个变量之间的独立性。在贝叶斯网络，其联合概率计算是由图来定义的，如下图1.所展示，而如果没有贝叶斯网络，我们无法了解各个变量之间是否有联系，就认为都有联系，于是列出的联合概率公式为0.所示。概率图模型基于图，而图这种数据结果分为两种：有向图和无向图，针对有向（无环）图结构，实现的是贝叶斯网络，针对无向图，则为马尔可夫随机场。
概率图模型的机器学习公式推导笔记
由于本次提供的信息中存在一定的不确定性，我将基于“概率图-详细笔记.zip”这一标题和描述，结合概率图模型在机器学习中的应用进行详尽的阐述。 首先，概率图模型主要分为两种类型：贝叶斯网络（Bayesian Networks...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值