Coursera机器学习基石笔记week14

Regularization

Regularized Hypothesis Set

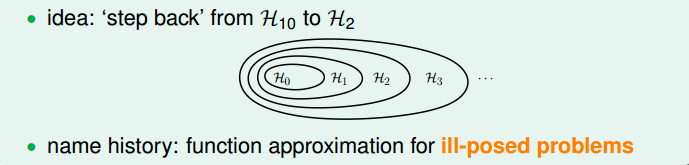
我们发现10阶多项式hypothesis set里包含了2阶多项式hypothesis set的所有项，那么如果我们加一些限制条件就可以让其近似为$H_2$。这种函数近似称之为不适定问题（ill-posed problem)。

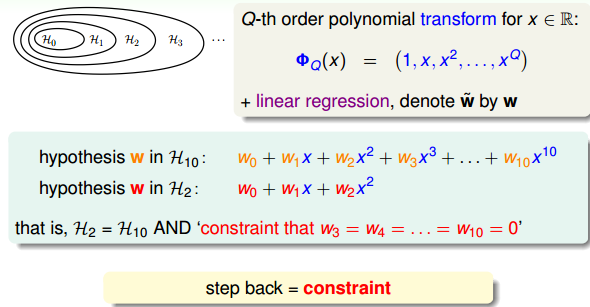
根据上图可知，我们令$w_3=w_4=.....=w_{10}=0$即可让$H_2=H_{10}$。通过将高阶的hypothesis转换为低阶的形式，可以有效的防止过拟合。

但是如果我们将$w_3=w_4=.....=w_{10}=0$全置0与直接使用$H_2$有什么区别呢？所以因此我们让这个限制条件变得更加宽松，不再要求$w_3=w_4=.....=w_{10}=0$，而是限制w不为0的个数，这种限制被称为looser constraint。

针对我们提出的这个新的hypothesis，我们将其称为sparse hypothesis。

但是对于我们提出的这个hypothesis，被证明也是NP-hard问题，因此我们尝试去找到一个易于求解的限制条件，这被称为Softer Constraint。

又一次，针对我们提出的这个新的hypothesis，我们将其称为regularized hypothesis。

Weight Decay Regularization

根据我们提出的regularized hypothesis，我们可以来了解一下最小化$E_{in}$的过程：

在原来没有限制的情况下，根据梯度下降算法，w就会往梯度的方向移动直到谷底，但是现在因为我们增加了限制条件。那么w只能局限在以原点为圆心，$\sqrt{C}$为半径的圆里。那么这种情况下，大概率是到不了谷底了，只能在圆上不断移动。我们假设上图蓝色箭头为梯度下降的方向，因为我们被限制在圆上，那么其实真正移动的方向就是上图绿色箭头所指示的方向，当梯度方向与绿色箭头方向垂直时，即与红色法向量平行的时候，说明梯度不需要在圆上移动，也就是达到了当前条件下的最低点。

因为梯度方向和w方向平行时，我们才能达到最优解。

因此$-\nabla E_{in}(w_{Reg})=w_{REG}$

但是我们发现上图中多了一个$\lambda$,其称为Lagrange multiplier，是用来解有条件的最佳化问题常用的数学工具，$\frac{2}{N}$是方便后面公式推导。那么我们的公式就变成了$-\nabla E_{in}(W_{Reg})=\frac{2\lambda }{N}{W}_{REG}$

那么我们的目标就变成了求解满足上述公式的w了。

我们知道线性回归的$E_{in}$的表达式为：

$E_{in}=\frac{1}{N}{\sum }_{n=1}^N(x_n^{T}w-y_n{)}^2$,

那么计算梯度代入我们上述的推导即可得到：

$\frac{2}{N}(Z^{T}Z{w}_{REG}-Z^{T}y)+\frac{2\lambda }{N}{w}_{REG}=0$

上式中包含了求逆矩阵的过程，因为$Z^{T}Z$是半正定矩阵，如果λ大于零，那么$Z^{T}Z+\lambda I$一定是正定矩阵，即一定可逆。另外提一下，统计学上把这叫做ridge regression，可以看成是linear regression的进阶版。

对于更一般的情况，例如逻辑回归问题中，$\nabla E_{in}$不是线性的，那么将其带入平行条件中得到的就不是一个线性方程式，$w_{REG}$不易求解。那么我们再重新审视一下我们推出的式子：

$\nabla E_{in}(W_{Reg})+\frac{2\lambda }{N}{W}_{REG}=0$

我们可以想到$\nabla E_{in}$是$E_{in}$的导数，而$\frac{2\lambda }{N}{w}_{REG}$也可以看成$\frac{\lambda }{N}{w}_{REG}^2$的导数。那么其实可以转化为求$E_{aug}(w)=E_{in}(w)+\frac{\lambda }{N}{w}^{T}w$的最小值。

该函数中第二项就是限定条件regularizer，也称为weight-decay regularization。我们把这个函数称为Augmented Error，即$E_{aug}(w)$。

如果λ不为零，对应于加上了限定条件，若λ等于零，则对应于没有任何限定条件，问题转换成之前的最小化$E_{in}(w)$。

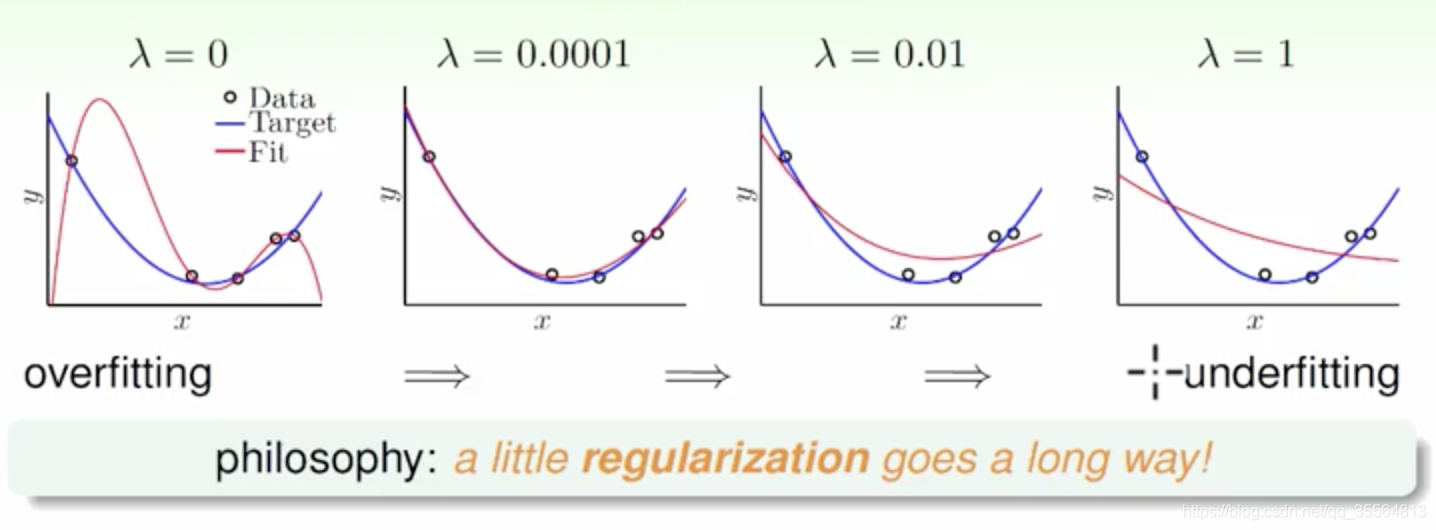
从图中可以看出，当λ=0时，发生了过拟合；当λ=0.0001时，拟合的效果很好；当λ=0.01和λ=1时，发生了欠拟合。我们可以把λ看成是一种penality，即对hypothesis复杂度的惩罚，λ越大，w就越小，对应于C值越小，即这种惩罚越大，拟合曲线就会越平滑，高阶项就会削弱，容易发生欠拟合。λ一般取比较小的值就能达到良好的拟合效果，过大过小都有问题，但究竟取什么值，要根据具体训练数据和模型进行分析与调试。

我们目前讨论的多项式是形如$x,x_2,x_3,\cdots ,x_n$的形式，若x的范围限定在[-1,1]之间，那么可能导致$x_n$相对于低阶的值要小得多，则其对于的w非常大，相当于要给高阶项设置很大的惩罚。为了避免出现这种数据大小差别很大的情况，可以使用Legendre Polynomials代替$x,x_2,x_3,\cdots ,x_n$这种形式，Legendre Polynomials各项之间是正交的，用它进行多项式拟合的效果更好。

Regularization and VC Theory

其中$w^{T}w$表示的是单个hypothesis的复杂度，记为Ω(w)；而Ω(H)表示整个hypothesis set的复杂度。根据Augmented Error和VC Bound的表达式，Ω(w)包含于Ω(H)之内，所以，$E_{aug}(w)$比$E_{in}$更接近于$E_{out}$，即更好地代表$E_{out}$，也就是泛化能力更强。
那么从另外一个角度我们也可以看到正则化的作用：

对于所有w都考虑的情况，那么vc dimension最大为d+1。但是随着引入了$H(C)$，
因为正则化的影响，使得w只取得了一小部分，那么随着w数量的减少，那么对应的自由度也减少了，那么对应的最大vc dimension会相应的减少。因为vc dimension的减小，我们就可以了解到对应的泛化能力更强。

General Regularizers

上图告诉我们，选择正则条件可以有三种选择

• target-dependent 基于目标的，比如需要奇数的，那么我们的条件就上需要奇数
• plausible：我们觉得有助于曲线更加平滑的
• friendly：容易进行优化的
  
  其实我们可以发现，这和之前讲的error measure的选择非常的类似。
  
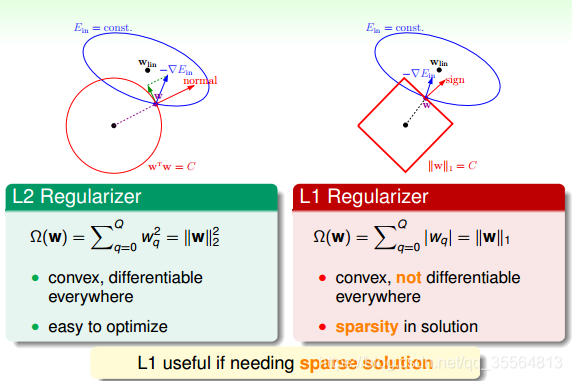
  L1计算的不是w的平方和，而是绝对值和，即长度和，也是凸函数。$E_{in}$常常不是与w的方向（红色箭头方向）平行的，那么w就会往顶点处移动，一般来说，最优解都会在四个顶点上,顶点处的许多w分量会为0，所以，L1 Regularizer的解是稀疏的，称为sparsity。优点是计算速度比较快。
  
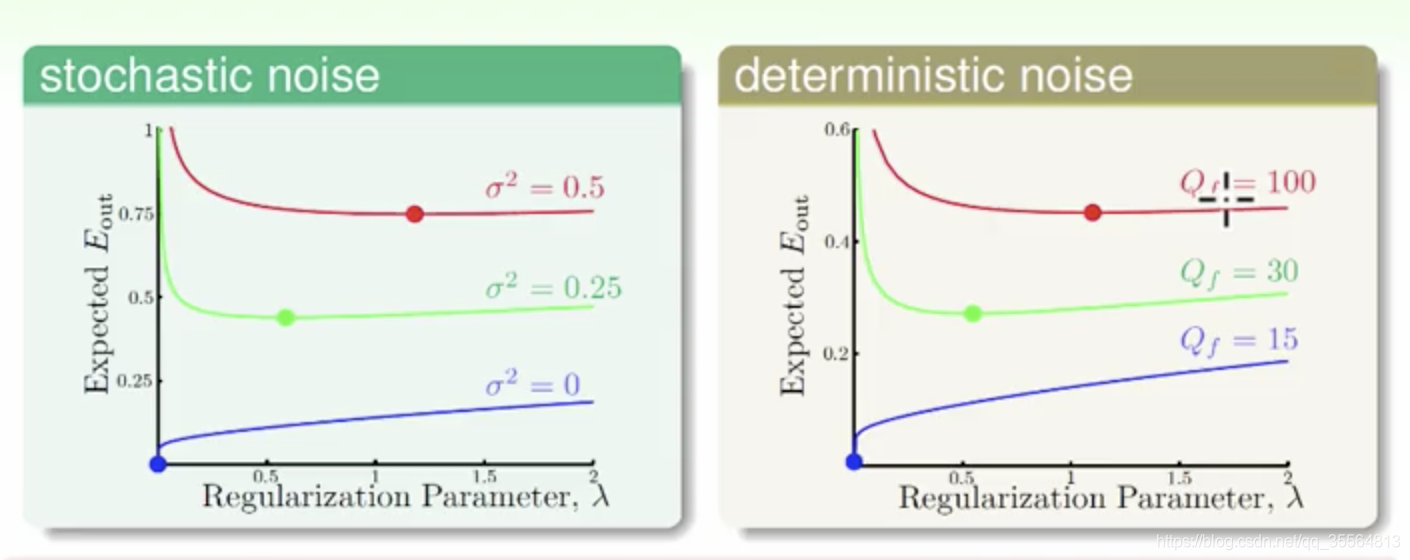
  从上图我们可以看出，越大的stochastic noise，所对应使$E_{out}$最小的$\lambda$越大，同理，越大的deterministic noise，所对应使$E_{out}$最小的$\lambda$越大。

总结

这节课主要介绍了正则化。首先在原来的hypothesis set上加上一些限制条件就引出Regularized Hypothesis Set。然后根据分析，又得出了相应的$E_{aug}$，然后也证明了$E_{aug}$导致的泛化能力更强。最后，介绍regularization是通用的机器学习工具，设计方法通常包括target-dependent，plausible，friendly等等。